Proof that the Lagrangian and the Hamiltonian are false

Lagrange

Abstract: The Lagrangian is perhaps the most important bit of math in current physics because it props up both celestial mechanics and quantum mechanics. In quantum mechanics, the Lagrangian has been extended into the Hamiltonian. The Hamiltonian does nothing to correct the Lagrangian, taking it as true and given. The proof that the Lagrangian is false in many situations has far-reaching consequences for physics, at all levels. A general discussion is first and then following this in the section Charge replaces Lagrange points yielding 3-body stability, the math will be shown.

At its simplest, the Lagrangian is just the kinetic energy of a system T minus its potential energy V

L = T – V

At Wikipedia, we are told this:
The Lagrange formulation of mechanics is important not just for its broad applications, but also for its role in advancing deep understanding of physics. Although Lagrange only sought to describe classical mechanics, the action principle that is used to derive the Lagrange equation is now recognized to be applicable to quantum mechanics.

What Miles Mathis will show is that the Lagrangian, rather than advancing a deep understanding of physics, actually blocked an understanding of the real fields involved. Because Lagrange (and Hamilton) misassigned the fields or operators, and because this formulation has been so successful and authoritative, many generations of physicists have been prevented or diverted from pulling this equation apart. What MM means by that is that, if we take Lagrange at his word, we would seem to have only one field here. In celestial mechanics, the gravitational field causes both the kinetic energy and the potential energy. In quantum mechanics, charge causes both the kinetic energy and the potential.

Let us start with celestial mechanics, since that is where the Lagrangian initially came from. The motions of celestial bodies are gravitational, we are taught, and the potential energy is gravitational potential. That being so, the Lagrangian must have originally been a single field differential. In other words, we are subtracting a field from itself. Our first question should be, is that even possible? Can you subtract gravity from itself, to get a meaningful energy? Or, to be a bit more precise, can you subtract gravitational potential from gravitional kinetic energy? That would be like subtracting the future from the present, would it not? Potential energy is just energy a body would have, if we let it move; and kinetic energy is energy that same body has after we let it move. So how can we subtract the first from the second?

Another problem is that for Newton, the two energies would have to sum to zero, by definition. This is clear for a single body, and a system is just a sum of all the single bodies in it. Therefore, both the single bodies and the system of bodies must sum to zero, at any one time, and at all times. In fact, Newton actually used this truism to solve other problems. He let potential energy equal kinetic energy, to solve various problems. But here, we are told that potential energy and kinetic energy don't sum to zero, and aren't equal, otherwise the Lagrangian would always be either zero or 2T. A Lagrangian that was always zero would be useless, wouldn't it, as would a Lagrangian that was just 2T. The objection to this statement is to say that Newton never summed T and V to zero, and no one else did either. However, the book (Physics , James S. Walker. Prentice-Hall 2002. p. 365.) says in the chapter on Gravity, subchapter on Energy Conservation on the problem of an asteroid falling directly to Earth:

Since gravity is a conservative force, the total mechanical energy remains constant as the asteroid falls toward the Earth. U Thus, as the asteroid moves closer to the Earth and U becomes increasingly negative, the kinetic energy K must become K increasingly positive so that their sum, U + K, is always zero.

Of course we can see that straight from the equations:

V = -GmM/r
K = GmM/r

If it is not those energies Lagrange is summing, which energies are it? What other energies does a body have in Celestial Mechanics? The mainstream cannot tell me E/M, since they have told us E/M is negligible in Celestial Mechanics. It might be suggested that a body can have sideways motion, as in an orbit, but since orbits also conserve energy—we are taught—the total kinetic energy must still equal K and still sum to zero with V . Otherwise the body would either be gaining or losing energy all the time, and the orbit wouldn't be stable.

Ignoring Celestial Mechanics, mainstream physicists are more interested in applying the Lagrangian and Hamiltonian to quantum physics, as in the Schrӧdinger equation. Since they have taught us that gravity is negligible at the quantum level, both V and T must come from charge or charge potential. In which case we should also have conservation, in which case we should have a sum to zero. They just forget all this when it comes time to derive the equations, and they let themselves say and write whatever they want.

We can see another problem in this quote from Wiki:
For example, consider a small frictionless bead traveling in a groove. If one is tracking the bead as a particle, calculation of the motion of the bead using Newtonian mechanics would require solving for the time-varying constraint force required to keep the bead in the groove. For the same problem using Lagrangian mechanics, one looks at the path of the groove and chooses a set of independent generalized coordinates that completely characterize the possible motion of the bead. This choice eliminates the need for the constraint force to enter into the resultant system of equations.

The problem there is that one solves by ignoring forces, looking only at the path. Why is that a problem? Because if you are studying the path and not the forces, you will come to know a lot about the path and nothing about the forces, which is what we see in current physics. The Lagrangian calculates forces by ignoring forces. It goes right around them. If that were just a matter of efficiency, it might be tenable, but we have seen that historically, the Lagrangian and action were chosen to avoid the questions of forces, which physicists were not able to answer. They weren't able to answer them in the 17th century and they aren't able to answer them now. So they misdirect us into equations that “summarize the dynamics of a system” by ignoring the dynamics of a system. Dynamics means forces.

We are told at Wiki that the Lagrangian is “a function that summarizes the dynamics of a system.” So here is yet another problem. We are then told that T is the kinetic energy of the system. Well, shouldn't the kinetic energy already be a function that summarizes the dynamics of the system? Dynamics means motions caused by forces, so the motion of the particles should be an immediate measure of all the forces on them. In other words, the gravity field should already be causing motion, so there is no reason to add or subtract it from the kinetic energy. Either the gravity field is causing motion, or it isn't. If it is, then it should be included in the kinetic energy. If it isn't, why isn't it?

But physicists have never bothered themselves with these logical questions. Why haven't they? Because they found early on that the Lagrangian worked fairly well in many situations. Like Newton's gravitational equation, it was an equation that they were able to fit to experiments. This is very important to physicists, for obvious reasons. But the fact that the Lagrangian worked meant that the kinetic energy and potential energy did not sum to zero, which meant that the bodies were not in one field only. To express energy as a differential, you must have two energies, which means you must have two fields. One field can't give you two energies at the same time. You cannot get a field differential from one field. As soon as the Lagrangian was found to be non-zero, physicists should have known that celestial mechanics was not gravity only. It had to be two fields in vector opposition.

By the same token, as soon as the Lagrangian was discovered to work in quantum mechanics, the physicists should have known that QM and QED were not E/M only. The non-zero Lagrangian is telling us very clearly that we have two fields. Just as gravitational potential cannot resist gravitational kinetic energy, charge potential cannot resist charge. Charge potential is not charge resistance, it is future charge. You cannot subtract the future from the present in an equation! This proves once again that gravity is present in a big way at the quantum level. (See Gravity at the Quantum Level.) This should have been known it just from the form of the Lagrangian.

Given that the Lagrangian is non-zero, and that it works pretty well, what can we infer from that? Just from the form of the Lagrangian, it can be inferred that we have two fields, in vector opposition, one field larger or smaller than the other, or changing at a different rate. We can infer these things, because logically they must be true.

What this means is that the Lagrangian was an accidental and incomplete expression of the unified field. The Lagrangian is a unified field equation. MM has already shown that Newton's gravitational equation was a unified field equation (See Newton's law is a Unified Field of Gravity and E/M), and that Coulomb's equation was a unified field equation (See Coulomb's equation is a Unified Field equation in disguise), and it turns out the Lagrangian is just one more unified field equation. Yes, both of the operators are misassigned or misdefined. The only reason the Lagrangian works is that the operation works, but it turns out the operation works only because of a compensation of errors. The equation has to be pushed to work.

The Lagrangian has sometimes been interpreted as the total energy of a field, so that it really is like adding the future to the present. The kinetic energy is energy the particle already has, the potential energy is energy it soon will have, therefore the Lagrangian is an expression of the total field present at a given location. If we want to know where a system is heading, we add its current state to its potential, right? Sounds feasible, but that isn't what is happening. The Lagrangian isn't a sum of present and future, it is a sum of energy due to charge and energy due to gravity. As with Newton's gravity equation, the Lagrangian already includes both fields. We can tell this just because the Lagrangian includes V, and V is a restatement of Newton's gravity equation. Since V is already unified , L must be as well. L is not a unification of present and future, L is a unification of charge and gravity.

So what is T, by this analysis? T is a unified field correction to V, since V doesn't contain enough information to solve. In MM's unified field papers, he has shown that although Newton's equation is fundamentally or roughly correct, it doesn't contain enough degrees of freedom to solve most real problems. It contains G, which tells us the scale between the two fields, but it doesn't tell us how the two fields vary by size. Newton's equation doesn't include the density of the charge field, which is relatively small at the macro-scale, but more important at the quantum level. In other words, because the photon has real size, it begins to take up more space at the quantum level. This makes the E/M field relatively stronger at smaller scales. It is a larger part of the whole at that level, and a smaller part of the whole at our scale. But Newton's equations have no way of including this information. The Lagrangian is an improvement, because T goes some way in solving this problem. The Lagrangian, on purpose or by accident, expresses this degree of freedom. This is because the “kinetic energy” term T includes the mass again. Not only that, but it tells us how that mass is velocitized by the fields present. We get the mass right next to its own velocity. Indirectly, this must tell us how that mass is responding to the photon density, which tells us how the gravity field and charge field are fitting together in this particular problem. So the variable T corrects the variable V , giving us a total field L energy that is an improvement on any energy Newton could find or predict.

What makes the Lagrangian sometimes wrong is that, when you have an equation that is in a confusing and unknown form, it is quite easy to plug the wrong information into it. In its current form, the Lagrangian is potentially useful, since if you do everything right, it will work. But since most or all physicists don't know how or why it is working, they end up plugging the wrong numbers into it.

We see this in the two-body central force problem, where the Lagrangian is used to make a hash of the problem. This is apparent at Wiki from the first sentence, which begins,

The basic problem is that of two bodies in orbit about each other attracted by a central force.

In the two-body problem, two bodies are not in orbit about each other. One body is orbiting the other body. Is the Earth orbiting the Moon? No. The Earth may or may not be orbiting a barycenter, but in no case is the Earth orbiting the Moon. Also, in the two-body problem, are the bodies attracted by a central force? No. Each body is attracted by the other body. There is no central force. The barycenter, even were it true, would be mathematical only. No force comes from there. We have seen this sort of language in many other places, and it is a bit shocking. How can physicists use such sloppy language? Actually, it goes beyond sloppy, since it is demonstrably false. This language is being used as more misdirection. It is used as a purposeful confusion, so that the reader cannot make sense of anything on the page. But the problems are not just problems of semantics or propaganda, they are mathematical, for we are then given the equation

L = T – V = ½ MṘ² + [½ uṙ² - V(r) ]

Where M is the combined mass, Ṙ is the velocity of the barycenter, u is the reduced mass, and ṙ is the change in distance between the two bodies (the velocity of the separation). That is a hash for so many reasons. One, if we put M and Ṙ next to each other in an energy equation, they have to apply to the same thing. One can't apply to combined mass and one to the barycenter. No, M must be the center of mass, not the combined mass. This means we MUST put the combined mass at the center of mass. But if we do that, then we can't have any separation, and if we don't have any separation, we don't have ṙ. The same thing applies to u and ṙ. To put them together in an energy equation, they have to apply to the same thing. One can't apply to one thing and the other to another. Therefore, ṙ should be the velocity of the reduced mass, not the change in separation. But since the reduced mass is a quotient over a sum, it can't have a velocity. And, since MM has shown on his site that reduced mass is a figment from the beginning, it can't be put into any equation. It is false, so it necessarily falsifies any equation it is in.

[To see a variant critique of this Lagrangian derivation, see MM's paper on his site on on Lev Landau's orbital math, where he pulls apart Landau's textbook proof of central motion—which is similar to this one. There, he shows further fudges in the polar coordinates, as well as the variable assignments in the equation above.]

But it gets even worse. Study that equation some more, and you see that it has not one but two kinetic energies in it. Thinking that the Lagrangian was already a summation, applying to a system, yet there seem to be two kinetic energies in there? Shouldn't a system have only one total kinetic energy? From the brackets we seem to be told that

V = -[½ uṙ² – V(r) ]

This does not make any sense because we are then told that

L = L_cm + L_rel

Assuming that this form implies L_rel = [½ uṙ² – V(r) ]
Unfortunately, that means that
L_cm is just a kinetic energy, with no potential energy component. Since when can you write a Lagrangian as just a straight kinetic energy? What possible least path is that action taking? It can't be a least or most path, since it can't vary. It is just one thing, and therefore cannot be pushed to into a least path.

Then we are told, “The R equation from the Euler-Lagrange system is simply Ma = 0 [where a is the acceleration of R, R dot dot], resulting in simple motion of the center of mass in a straight line at constant velocity.” One does not need these equations or the Euler-Lagrange system to tell us that! Of course the center of mass is going to have an acceleration of zero, since you can't have a force there by definition. That is why we found a center of mass in the first place, for Pete's sake. This author at Wiki implies that he found the zero acceleration via these equations, but the zero acceleration was the postulate, so it cannot be the discovery. The mass causes the force, by definition, and the force causes the acceleration, by definition, therefore you cannot have acceleration at the center of mass (any more than you can have acceleration at the center of a single body). That is what center of mass means, by god.

But it gets even worse. We have already seen L_cm reduced to an idiotic tautology, now we also must see L_rel reduced to a rubble of finessed math. For the equation is then expanded via polar coordinates to this

L_rel = ½ u(ṙ² + r²ω²) – V(r)

Where ω is the velocity or change in θ. Since Lrel is not dependent on θ, θ is an “ignorable” coordinate, we are told. It is ignorable, and there is “no dependence,” which seems to be a great reason to find a partial derivative of L_rel with respect to it.

∂L_rel/∂ω = ur²ω = constant = l

And of course l is the conserved angular momentum. You have got to be kidding me. That's just pretend math, right? That equation was inserted as a joke by some mischievous math elf, right? No, apparently mathematicians and physicists really buy this stuff.

At least we can see why some of the previous equations were manufactured. We needed to get something we could differentiate into uvr or ur²ω . That is just the old angular momentum equation L = mvr. But it doesn't explain what happened to the potential energy, which just got washed down the drain. Since there is no angle in the potential energy, V(t) just conveniently got jettisoned.

The only reason to take a partial derivative of L_rel with respect to that angular velocity is to push this equation, but there is no mechanical justification for it. First of all, differentiating requires a dependence. Remember first year calculus, where you were told what a function was? A function is a dependent variable, and in order to do calculus, you require dependent variables. Calculus requires functions, which requires dependence. But here they admit that the Lagrangian is not a function of the angle, then they differentiate the Lagrangian with respect to the angular velocity! Incredible chutzpah.

Beyond that, MM has shown that angular momentum is not equal to mvr or mr²ω, which means all this equation finessing was in vain. Someone should have told them the historical angular momentum equations were false, so they could push these equations toward the right ones, thus it makes it easier to see the cheating. Clearly they were just pushing the equations toward what they thought they needed.

Now let us return to the Lagrangian for celestial mechanics. It is clear that the Lagrangian is a poor or partial attempt to express the unified field. It is useful to compare the Lagrangian with MM's UFT. Let us use my force equation, to start with

F = (GmM/r²) – (2GmM/rct)

That already looks a lot like the Lagrangian, doesn't it? Let us multiply both sides by r, as they do now, to make F into E. That gives us

E = (GmM/r) – (2GmM/ct)
since GM = ar²
E = (GmM/r) – (2mar²/ct)


and since ar = v²
E = (GmM/r) – (2mv²)(r/ct)

Now it looks almost exactly like the Lagrangian. It can also look like the Hamiltonian:

p = mv
E = (GmM/r) – (p²/2m)(4r/ct)

The term r/ct is just a simple Relativity transform. My unified field equation is already both unified and Relativized.

Thus, the Lagrangian and Hamiltonian are variants of my unified field equations. The only difference is that MM would never have put an orbital velocity into a kinetic energy equation. That is what we had to do, as you see, to get the Virial from my unified field equation. (See The Virial Theorem is false on MM's site.) But since we see the mainstream do stuff like this all the time, we know this is how the Lagrangian and Hamiltonian got into the sloppy form they are now in.

Let me clarify that. Velocity is a vector, so in the kinetic energy equation T = ½ mv², it must be linear. But in the equation a = v²/r, the velocity is not linear. The velocity there is orbital. Therefore, that substitution MM used was not really allowed. Even if you allow him to correct the equation, so that it is now a² = v²/2r, the velocity is still not linear, and the substitution is still not allowed. In that correction, the velocity is still orbital, not tangential. To use a kinetic energy equation in the form ½ mv², we have to use a linear or tangential velocity.
as shown in MM's corrected equation for tangential velocity is
v² = a² + 2ar, which would make the above substitution
a² + 2ar = 4GM/ct, dooming the move from unified field to Lagrangian.

[See Rewriting the Schrӧdinger equation where MM replaces the Hamiltonian with he UFE by going here .]

What does that mean? It means that although T looks sort of like a kinetic energy in the Virial and Lagrangian, it isn't. In both celestial mechanics and quantum mechanics, you have to force fit the current equation to make it work. In celestial mechanics, you have to pretend that you can put an orbital velocity into a kinetic energy equation, but you can't. T isn't really the kinetic energy, it is just a term that mimics the kinetic energy in form. The Virial and Lagrangian aren't really using the kinetic energy and potential energy, they are mirroring the terms of my unified field equation, and my terms aren't standing for kinetic energy and potential energy. They aren't even standing for charge and gravity. They are just two terms in the equation, unassignable directly to any real field or energy.

This means that if you use a real linear velocity in the Lagrangian, you are going to get the wrong answer. You actually have to use a bad or false expression for the kinetic energy to get the Lagrangian and Virial to work. You have to use a false substitution, of orbital velocity for tangential velocity, to make the Virial or Lagrangian work. This is what MM meant when he said you had to push the Lagrangian in the right way, above. You have to insert the proper numbers, which turn out to be fake kinetic energies, expressed with orbital or curved “velocities” instead of real linear or tangential velocities.

To see what MM means, we have to go back to the equations leading up to my unified field equation. These are taken from Newton's law is a Unified Field of Gravity and E/M.

F = E + H
F = (GmM/R²)(1 – 2R/ct )
F = (GmM/R²) – (2GmM/Rct)

E is the charge field and H is the solo gravity field. F is the unified field. But neither E nor H is expressed by GmM/R². That term is just Newton's equation, which was already unified. The other manipulation here is just my correction to Newton. That correction was found by segregating the two fields, then doing relativity transforms on both separately, then recombining them. So the term 2GmM/Rct is a correction, not a field. It is not the charge field, it is not potential, and it is not kinetic energy. But the Lagrangian is mimicking this equation, as MM has shown. V is mimicking the first term, and T is mimicking the second, so that the Lagrangian is really this equation in disguise. is not the kinetic energy, T is this correction to Newton.

And this has been another major problem with unification. Physicists since the time of Einstein have been trying to unify QM with gravity, but since the equations of QM are grounded by the Lagrangian, QM is already unified. Not realizing this, physicists try to unify their Hamiltonians, connecting them in various ways to GR (General Relativity). As MM has just shown, this can only cause a mess. Everyone is trying to unify equations that were already unified. The reason they don't know this is that the Lagrangian was fudged, centuries ago—pushed to match data—and the push just accidentally matched fairly closely the unified field equation.

Yes, we can now see for certain that the equation finessing by Lagrange and Hamilton and the rest was completely accidental. We know that they didn't realize the equation was a UFT, because if they had known that, they wouldn't have later tried to unify it.

In conclusion, we have learned many things about the Lagrangian. One, the variables are misassigned. V is not potential, it is Newton's gravity equation, which was already unified from the beginning. And T is not kinetic energy. T is simply a term that corrects V as in my unified field equation. is a correction to Newton's F. It just happens to mimic the form of kinetic energy. But to make T work in T the Lagrangian, you have to insert an orbital velocity for v. In other words, you have to insert a falsified kinetic energy. If you push the equation in the right way, you may get the right answer. But in most cases, the Lagrangian is just used as a fudge, as in the two-body problem.

In a subsequent paper, MM will show that T also has to be pushed when the Lagrangian is used in quantum mechanics. If you use a real kinetic energy, rigorously defined, the Lagrangian and Hamiltonian fall apart. The only way to make them work is to use a fake “kinetic energy”, one that has been pushed to match my unified field equation.

This means that we should dump the Lagrangian and use MM's unified field equation instead. Once we fix all these errors with MM's UFE, we will be able to see the mechanics and fields underneath our equations. If the form of MM's UFE is not what is needed for certain problems, it can be easily extended into other forms, some of which MM has already provided . Using MM's UFE will allow us to solve many problems that have remained insoluble, at both the quantum and the celestial levels. My UFE brings the charge field into the light, with all its mechanisms, and a hundred problems have already fallen to its clarity.

Charge replaces Lagrange points yielding 3-body stability

Abstract: In this paper MM will continue to extend his unified field, and more specifically my charge field, to explain other current anomalies. As MM has done in the past, he will solve both anomalies that are admitted to exist and anomalies that are not admitted to exist. Here it will be shown that the current Lagrange points are misplaced in the field, due to mathematical errors by Lagrange. By re-running the 3-body problem with MM's simple unified field equations, new points of balance for the Moon will be shown and for a satellite like SOHO; but also the precise places where the current math and theory fail. MM will also pull apart the Lagrangian, showing that although it is claimed to represent action, or a sum of potential and kinetic energy, it is actually trying to represent MM's unified field, with gravity and charge. This shows that the equations of celestial mechanics continue to fail not because of chaos, but because of simple and longstanding errors. Lagrange failed to identify the charge field in the equations of Newton and in the data, and he failed to see how the field varies as it moves in and out from the Sun. Without that knowledge, he could not get his operators to work. He could only push them, and we continue to push them to this day.

We are taught that Kepler showed all orbits are ellipses, and that even the round ones are very slightly elliptical or eccentric. In Solution to the Ellipse problem it is shown that current orbits, either circular or elliptical, are not supported by the historical fields, neither those of Newton nor of Einstein (nor, as you will soon see, of Lagrange). Although physicists can write tortuous equations for orbits, they cannot explain their causes. Lagrange, along with Euler and Laplace, recognized this early on. As a preview on Lagrange see on MM's site Laplace and his equations. Lagrange discovered that in real life, Newton's fields and physical explanations did not work and nor did Laplace. If we have just three bodies, Newton's equations show a necessary instability. Since we know that three-body problems have a real solution and a high degree of stability (think the Moon), Lagrange needed to find a way to write new equations, which he did. However, he never fleshed out Newton's physical field, to show how the mechanics caused the math. We have had a hole in celestial mechanics ever since, though it doesn't seem to bother many people.

Rather than sum forces in the three-body problem, Lagrange summed kinetic and potential energies, creating a thing called action. Action is the "least motion" in these two fields. Yes, by looking at both potential energy and kinetic energy, Lagrange was able to extend Newton's one field into two. He created a sort of unified field, with two parts. But since potential and kinetic energy both seem to come from the same underlying field of gravity, it was thought he had only performed some sort of mathematical trick, creating two degrees of freedom where there was only one before. In a way, that is precisely what he did. He waved his wand and created a field out of thin air, without any mechanical or physical assignment. He and everyone since has either run past the problem, or they have assumed that his potential and kinetic energies are both explained by Newton's gravity field, but they are not.

What Lagrange actually did is intuit the solution, then write math to fit it (as we all do occasionally). He saw what the answer must be, then found a dual field that would allow for or cause the degree of correctability that he saw must exist in the orbit. This is why his equations have been so successful, and why physicists have not wanted to analyze them too closely for bugs. Don't look a gift horse in the mouth, you know, especially after he has won the Kentucky Derby.

Murray Gell-Mann, one of the fathers of quantum chromodynamics, put it this way when explaining how QCD worked as a math:

In order to obtain such relations that we conjecture to be true, we use the method of abstraction from a Lagrangian field-theory model. In other words, we construct a mathematical theory of the strongly interacting particles, which may or may not have anything to do with reality, find suitable algebraic relations that hold in the model, postulate their validity, and then throw away the model.

This is very interesting, because it means that the top physicists have always understood that the Lagrangian math is a method of abstraction that may or may not have anything to do with reality. Whenever anyone says "may or may not", you may read "may not." Whenever anyone says that, you may assume they don't really care one way or the other. Lagrange, Gell-Mann, and all the rest have made it very clear that they do not care whether any of their maths match reality. All they want is a number at the end that matches data: they could care less about physics. Modern physicists preen themselves on this attitude, but any sensible person must find it strange to see physicists bragging that they do not care about physics. This is what Gell-Mann is telling you here, in very clear sentences, and he is like all his modern precursors, all the way back to Lagrange. They are looking for "suitable algebraic relations" only. But even in this, they fail. The most suitable algebraic relations are relations that match reality, so you cannot sniff at reality. Physicists now pretend they don't care about reality, but that is only because they haven't been able to shake its hand. It is like the monk claiming he doesn't like girls anyway.

Unfortunately, the equations of Lagrange (and those of Laplace) did contain some remaining glitches, which led to perturbation theory, chaos theory and so on. An even bigger glitch is that he never bothered to define or explain the physical genesis of this second degree of freedom or his second field. Whereas, failing to assign your fields like this is not a metaphysical error, it is a physical error AND a mathematical error. Rather than admit that, all assumed that this field assignment was not important, since Lagrange assured everyone it was just potential energy. Since everyone had equations for potential energy already, they assumed this was the familiar old potential energy of Newton, just a by-product or restatement of gravity. Since they had familiar equations for potential, they forgot to ask questions about it.

For those situations when Lagrange's unified field is working were when it parallels MM's unified field Newton's law is a Unified Field of Gravity and E/M, where charge is the second field. And when Lagrange's unified field isn't working, it is because it is not paralleling my unified field. In other words, his sum was an approach to the correct field math, but it wasn't quite the correct field math. MM's unified field theory has finally provided a method that is so good at explaining the motions that we do not even need chaos theory or perturbation theory anymore. Once you replace his kinetic energy with charge, and fix Relativity (See An Algebraic Correction to Special Relativity and Refutation of Gamma), there is no remaining error.

Yes, it is the kinetic energy of Lagrange's equations that was unassignable. In his equations, it is the potential that is standing for the gravity field, and kinetic energy is physically unassigned. Some will be shocked by that, and others will not understand what MM means. So he explains it in full detail. Since the time of Newton, gravitational potential and gravity had been two expressions of the same field, one simply the reverse of the other. When MM says that they were the same field, he means that they had the same mechanical cause. Newton's gravity field was a mass field, and the mass caused both the gravity and the potential. But Newton wrote the equations as complements of one another, and for him they always resolved. That is why he called it potential. Gravitational potential energy was just energy that would be expressed kinetically if you allowed an object to move in the field, by the field. So kinetic energy and potential energy weren't really two separate things. One was gravity being expressed by motion, and the other was gravity about to be expressed by motion.

To give an analogy, say you are about to take a walk. You can say, "I am about to take a walk." That is potential. It is in the future. Then you take the walk, and while walking you say, "I am walking." That is kinetic and present. But you only took one walk. Only one parcel of energy was expended and only one distance was covered. So you cannot sum potential and kinetic energy in a gravitational field. You cannot sum those two sentences above. You cannot sum the future with the present, and claim you have two different things. This is how Lagrange cheated.

Let me restate that, for good measure. In the Lagrangian, the potential and kinetic energy don't resolve. If they did, the Lagrangian would always be zero. For Newton, any sum of potential and kinetic energy would have equaled zero, by definition, since the one field creates them both and since one is the physical inverse of the other. But Lagrange discovered, to his eternal credit, that the two don't resolve, in fact. A celestial body has kinetic energy that can't be explained by the gravity equations or the potential. In other words, there is more to the field than just mass and distance. Once we have exhausted the potential, we still have kinetic energy left over. Given the definitions of Newton, that can't be. What this should have told Lagrange is that there is another mechanism at work in the field, to give us that residual kinetic energy. Something else is driving celestial bodies besides gravity. The very fact that the Lagrangian is not zero is proof of a second field of some sort. But Lagrange never bothered to notice that, or if he did, it was ignored. He buried the field mechanics under a successful math, and no one has taken the time to dig the physics out of the math since then.

What this all means is that Lagrange had a hidden unified field, just like Newton. Newton's unified field was hidden in G, and Lagrange's unified field is hidden in the Lagrangian. It is hidden in the fact that the Lagrangian is not zero. There is a residual force not accounted for in the field mechanics. The math is hiding a large part of the field.

Lagrange's equations often work, and they work because they create a field out of thin air. They magically double a single field, by taking a thing and its shadow as two different things. But as it happens, there was a real field there, invisible to Lagrange and everyone else, and his equations expressed it fairly well. The charge field was there. Not only was it there, but it was already inside Newton's gravity equations, and no one knew that either. The second field was there, it was hidden inside the constant G, and what is more, it was aligned opposite to solo gravity, as a vector. In other words, it was a differential, not a sum. The Lagrangian is not really a sum, it is a differential, since potential energy and kinetic energy are arrayed opposite to one another as vectors. You subtract. Well, you do the same thing with charge and solo gravity, so the Lagrangian is pretty good math in that regard. Lagrange understood that he needed a differential in order to create the correctability. You have to have two fields working in opposition in order to create that degree of float that we see in real orbits.

However, Lagrange made many big errors. (See the paper on the Virial on MM's site , showing that the biggest standing error in the Virial and the Lagrangian is an extra 2 in the field equations. According to the math of Lagrange, you can fall to the center of a gravity field and still have half your potential left. The reason he has that huge error in his math is that he borrowed Newton's math without analyzing it, and Newton's math already contained that huge error. It was already embedded in the equation a=v²/r, and Lagrange didn't spot it. According to Newton's own variable assignments and math, it should have been a=v²/2r. (See A Correction to Newton's Equation a=v²/r. Lagrange hid Newton's error and physicists since Lagrange have hid his errors.

You can see that without even reading my paper on that orbital equation, since the Lagrangian has always had that unexplainable 2 in it. If you don't like my explanation of why it is there, you tell me why it is there. It conflicts loudly with Newton, but no one deigns to notice that.

Lagrange also performed some shocking cheats with the calculus, as shown in at the end of this paper: The Calculus Is Corrupt. He did a switcheroo in front of everyone's eyes, like a man with three shells and quick hands, and nobody has spotted the switch in all these years. But you will have to read that paper to see the trick.

Anyway, anytime you have fundamental equations with extra twos in them, you are going to get chaos. You are going to get physicists trying to push the equations and pinch them and Jerry them to match data, which is what we have seen. We have seen centuries of embarrassing pushes and fudges, and the entire field of Chaos theory is based on this fudge. Same for most of perturbation theory, and other large areas of current physics. If we removed all the subfields of physics that were created to push faulty equations like this into line, we would have to remove at least 75% of the field as a whole.

Notice that in the Virial, which leads to the Lagrangian, the potential energy is twice the kinetic energy. The problem with that is this implies Lagrange's invisible second field is the same size as his visible field. Lagrange has written an equation in which the charge field is the same size as the gravity field. MM has shown that is not physically true. Or, it is true only for objects of a certain size. It is true for objects that are around 1 to 10 meters in diameter. This is why the Lagrangian works well at the human scale. But for smaller and larger objects, the Lagrangian is false. Lagrange has correctly found the two degrees of freedom in the field, but he has not combined them correctly, because he didn't know the mechanics of the two fields. To know how they combine physically, you have to know what is causing the motions in each field, and Lagrange didn't know that. Nobody has known that until now. So the Lagrangian was a step in the right direction, since it gave us a dual field, with one field in vector opposition to the other. But the Lagrangian is still incomplete, since it doesn't combine the two vectors in the right way. As we know, the charge field diminishes as a fraction of the whole as we go larger, and increases as a fraction of the whole as we go smaller. The Lagrangian doesn't include that fact in the math. In other words, radius matters, and the Lagrangian fails to incorporate that variable in the right way. There is a third degree of freedom in the math caused by the freedom between the two fields. There is a size variation in the way the fields stack, and that is a third degree of freedom in the math.

One way that Lagrange's orbital equations are semi-successful is in their prediction of Lagrange points. Jupiter's Trojans are cited as proof of this success, and that is in indeed what is happening with the Trojans. They are inhabiting areas where the field more or less balances. However, this has nothing to do with kinetic and potential energy, it has to do with gravity and charge. Neither kinetic energy nor potential energy can hold real objects at a distance, and the only way that the Trojans can be kept from moving closer to Jupiter is with some real force of exclusion.

Some will say, "What do you mean, kinetic energy cannot keep things at bay? That is precisely what does keep things at bay!" No, Lagrange must mean gravitational kinetic energy, and gravitational kinetic energy does not keep anything at bay. Gravitational kinetic energy has no exclusionary power, by definition. Gravitational kinetic energy is the energy a body has due to the field, and that energy is always toward the central object. So the vector is wrong. There is no possible gravitational kinetic energy that could be keeping the Trojans from moving closer to Jupiter. Gravitational kinetic energy is always toward an object, not away from it.

We can say the same for potential energy. Potential energy has no exclusionary power, which should be obvious.

The Trojans must be excluded for some other reason. Some other field must be balancing the gravitational field here. Which means that the Trojans are just one more proof of my unified field, and of charge. The Trojans are held at bay by the charge field of Jupiter.

We can see this most clearly if we go to Lagrange point 1, instead of 4 and 5. It is known that Lagrange's points 1 and 2 don't really exist where they are supposed to. We have tried to take satellites to the Earth's point 1, with no success. The satellites are there, but there is only a reduced instability, not a stability. Not only is there no stability there, there is no stability around the point. The most stable orbit in the area is the halo orbit near point 1, where the Solar and Heliospheric Observatory (SOHO) exists. But even halo orbits aren't stable, and they require station keeping or governors. The same is true of Lissajous orbits, which means that Lagrange's equations are only generally correct. He sends us to the right general area, but not to the right point, and not with the right governors. We haven't really solved the field equations yet, because we don't understand the make up of the fields. The engineers know this, but they are kept quiet by the theorists. The engineers push the equations to make them work, and then they are told to stay mum about it. By recalculating point 1 below with MM's unified field, shows the errors in the current math. It turns out that Lagrange's equations don't even send us to the current Lagrange points without a lot of very unsightly tinkering.

First, let's compare the Earth's points 1 and 2 to the motion of the Moon. It seems to me that a single Moon would try to hit those points, since it would be a great energy saver if it did. Action is supposed to be "least motion", which would imply an energy saving like this, but according to the current math the Moon ignores the points, orbiting well inside them. That is the first sign something is wrong with the equations.

Next, let us look at the eccentricity of the Moon. According to current equations, the Moon should have an eccentricity of infinity and should crash into the Sun. (See Solution to the Ellipse problem.) They don't admit that, of course, and if you show the imbalance in the equations, they point to the sum, which resolves. But the problem is not the sum, it is the individual differentials. At New Moon the Moon is seriously out of balance, for instance, and although it corrects that, there is no physical explanation of how it corrects that. In other words, the current equations are garbage. They are pushed. They resolve only as a sum. As a theory or a mechanics, they miss by infinity.

We find the Moon has an eccentricity of .055, and, again, current equations can show that only with a major push. As we will see below with the Lagrange point math, physicists switch to non-inertial math and bring in centrifugal forces and Coriolis forces and so on. This despite the fact that gravity is inertial. Gravity practically means inertial, and yet they have the gall to hide in non-inertial math. Even worse, they claim to do non-inertial math, but then propose Coriolis forces and centripetal forces inside this math. The problem there? Forces are inertial, by definition. Going to non-inertial math and then proposing new forces is absurd. It is somewhat like an ichthyologist doing all his research on dry land, and then writing equations for buoyancy with solid state equations, instead of liquids.

Most won't understand what MM's mean by that either, so he elaborates. Historically, non-inertial has just meant any situation that includes accelerations, so gravity seems non-inertial. That is what people are taught, so that is all they know. But gravity isn't non-inertial, since gravity doesn't avoid inertia. It only avoids the easy solutions, and it only avoids them because mathematicians have preferred to muck up the math. Gravity is inertial for two reasons: 1) it is a field of forces, specifically centripetal forces, and forces are inertial. You can't have gravity without inertia and you can't have inertia without gravity, so gravity is inertial. You will understand if you consider that in the end, Einstein considered his field equations to be non-inertial. But by that he didn't mean that they included accelerations; no, he meant they bypassed accelerations. In curving his field with new math, Einstein got rid of centripetal accelerations. It was the curves that caused the motions, not the force. So what non-inertial really means in General Relativity is no forces. It means curves rather than forces. 2) Gravity is inertial because the line of influence between two bodies is a line, not a curve. Even AFTER Einstein made his field non-inertial in both ways, the line of influence was still a straight line. That is the one line that non-Euclidean math doesn't make into a curve. Since gravity works along that straight line of influence, gravity is inertial for Newton, and it is inertial for Einstein. Both of those guys, and everyone else since, has tried to deflect you from seeing that, but it has always been true and still is. Gravity is inertial because it concerns forces; and gravity is inertial because it can be solved along straight lines. You have been taken into curves and other non-inertial math because the old guys couldn't solve this one in a straightforward manner, so they decided to hide in big equations. Why couldn't they solve it? They didn't have that second field. Even after Lagrange gave them a second field (kind of) with the Lagrangian, they forgot to assign it to something real. If they had recognized that the second field was not potential, they might have been able to unify long ago. Instead, they have had this "successful" math sitting around for centuries, and never thought to look for the E/M field inside it. It never occurred to them that charge, electricity and magnetism had already been included in the Lagrangian from the beginning.

If we go back to the eccentricity of the Moon with all this in mind, we can solve it. In Tides are caused by E/M field not Gravity MM shows that tides are can be calculated from an E/M effect. If we know how the field really works, we can solve such problems without any difficult math at all. All we need is fractions. Yes, the Solar Wind at the distance of the Earth/Moon is strong enough to positively affect the Moon's orbit. Not only is charge an effect of the unified field, but secondary effects of charge also have to be factored in, like the Solar Wind in Spring and neap tides are caused by the Solar Wind.

Another oddity of current math concerns the spreading of Lagrange points. We are told that ellipses cause Lagrange points to spread out or blur, but that is just rationalizing. It is especially sad regarding points 1, 2, and 3, which are in a line. How can an ellipse spread that math? It isn't that the Earth's eccentricity spreads or hides point 1, for instance, it is that the satellites are in the wrong place. They are thousands of kilometers away from the true points of balance, and so they require halo orbits and governors to overcome the forces they still feel. MM will prove that below.

Now MM recalculates Lagrange point 1 for the Earth. MM has done similar math in his papers on his site on weight and on the magnetosphere, showing where the two fields balance. According to current math, Lagrange point 1 is about 1.5 million km from the Earth. To find that, at Wiki we are currently told this
L₁ is about 1.5 million kilometers from the Earth. Gravity from the Sun is 2% (118µµm/s²) more than from the Earth (5.9μm/s²), while the reduction of required centripetal force is half of this (59μm/s²). The sum of both effects is balanced by the gravity of the Earth, which is here also 177μm/s².

See, no Lagrangian there. Notice how that looks a lot like tidal math. "The reduction of the required centripetal force" means they are calculating a centrifugal force, caused by the angular momentum, and it is half the main force. Funny that they include that here but not in the tidal equations for the Earth. As MM showed in his tides paper, they "forget" that the Earth is orbiting the Sun, so that they can force the number 46% to appear. Or, if they include it, they then use the same equation on the tide from the Moon, which would imply that the Earth is also orbiting the Moon. If you correct their fudge there, the number is 67%, which doesn't match data.

But here, they include it when they have no mechanical justification for it. The centrifugal effect or the "reduction of centripetal force" (which is supposed to be the same thing, MM assumes) might possibly enter the tidal math in a logical way—supposing the Earth were on a string tied to the Sun—because the centripetal and centrifugal forces oppose in a way that would pull on a real object, stretching it radially. But the centrifugal force can't be used here as they are using it, since it doesn't just "reduce" the centripetal force. They both have to act on the body, which will stretch it. Notice that is not what is happening here. They aren't applying both the force and the reaction to the force to the real object in the field, they are just subtracting out the reaction before any forces are applied! That is a cheat of magnificent proportion. Newton is turning over in his grave. The centrifugal force isn't an automatic "reduction" of the centripetal force, it is a reaction to it. This is because the centrifugal force can cause stretching, but it can't cause motion in the field. It is force felt internally by the object, and so it can't cause motion.

The same force can't cause two field effects. The centrifugal force can't cause a tide and also cause a field vector. It is either expended internally or externally. The centrifugal force is the body's own reaction to the orbit, and so it is not part of the field equations.

To make this even clearer, notice this contradiction: if the centrifugal force were a field response (instead of a response internal to the object) to the centripetal force, and if we could thereby add or subtract it from the centripetal force in the field equations, then we would create an infinite feedback mechanism. Say the centripetal force is x, and the centrifugal force is x/2, which we add, achieving 3x/2. Does the body now feel 3x/2? And if so, why doesn't the centrifugal force increase to respond to half of that?

In a Newtonian orbit, the body orbits because it is feeling a centripetal force. It is not orbiting because it is feeling a centripetal force plus or minus a centrifugal force. For Newton, the centrifugal force was included in tidal equations, but it would not have been included in these Lagrange point equations, for strictly logical and definitional reasons. MM finds it extremely sad that hr has to be here telling anyone this.

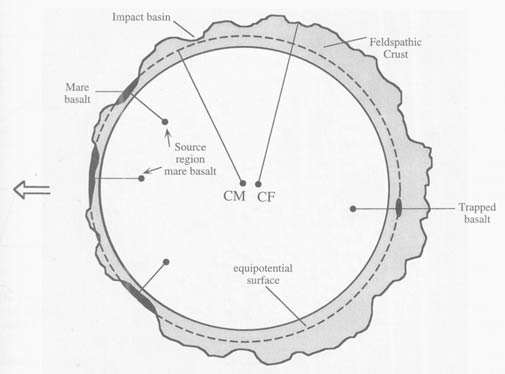
Not only is including the centrifugal force illogical as a piece of Newtonian mechanics, but we know from data that celestial bodies don't feel centrifugal forces. We have mountains of evidence that they do not, straight from the Moon. MM has been screaming about this evidence for years. Rather than argue about whether the Earth shows centrifugal forces in its tides, we can go to the Moon, where we don't have to look for fleeting evidence in liquids. We can look for evidence in the crust. Since the Moon is in tidal lock, the forces don't travel. Therefore they should stack, year after year after millions of years, making the evidence obvious. If we had centrifugal forces, we would see their effects on the Moon. We would see a big tide at the front and back, and we would see shearing sideways, one direction forward and one direction back. What do we have? The most glaring negative data imaginable. No tide in the back, and a negative tide in the front. And no shearing. We also have negative data that is very easy to read from the moons of Jupiter and Saturn, including the very small moons inside the Roche limit. But MM has covered those extensively in another paper on his site.

So the current math is a complete misunderstanding and misrepresentation of the field. Let's return to the Lagrange point math. M does not even understand where the numbers at Wiki come from. The number 177μm/s² above comes from this equation

a_E = GM_E/R²

But where does the number 118 come from? The gravity from the Sun at that point must be

a_S = GM_S/(1AU – 1.5 million km)² = 6082μm/s²

The Sun's gravity is not 2% more than the Earth's, it is 3400% more. Even with some jerryrigged centrifugal force, or reduction in centripetal force, we can't get those two numbers to balance.

Wikipedia is normally bursting with university people to correct things like this and/or defend them, but even on the discussion page MM found nothing. No one else found those two sentences strange, although they aren't even readable. Beyond the numbers, the sentences make no sense. Why are the Wiki police letting that stand? Do they really believe math or the English language is represented there? To find out, MM went to a university site:
(http://www.physics.montana.edu/faculty/cornish/lagrange.pdf) This site linked to the "full math". The full math started out like this:

The procedure for finding the Lagrange points is fairly straightforward: We seek solutions to the equations of motion which maintain a constant separation between the three bodies. If M₁ and M₂ are the two masses, and r₁ and r₂ are their respective positions, then the total force on a third mass m at position r will be

F = GM₁m(r - r₁)/(r – r₁)³ - GM₂m(r - r₂)/(r – r₂)³

The catch is that r₁ and r₂ are functions of time, since M₁ and M₂ are orbiting each other.

This is used as an excuse to bring in not only a centrifugal force, but also a Coriolis force! Notice that we are being misdirected here just as at Wiki, although the misdirection here is done with more finesse. That equation is a straight expansion of the math MM just did, but it has been mucked up to make it seem more complicated than it is. Why the cubes? Why the point coordinates and vectors instead of just distances? Also, when we look at the Lagrange points 1, 2, and 3, r₁ and r₂ are not functions of time, or, if they are, it doesn't matter to the math. We don't have to "adopt a co-rotating frame of reference in which the two large masses hold fixed positions." This is because M₁ and M₂ are not "orbiting each other." M₂ is orbiting M₁, and M₁ can remain fixed. All this math is just deflection, to get the reader confused. If the reader is confused enough by the math, he won't notice that it doesn't make any sense.

The only way that r₂ is a function of time is if we have to include the eccentricity of M₂. But we can estimate a solution without that, since the Earth's eccentricity is low. And if we estimate a number, it is nothing like the number from this full solution, with Coriolis effects and so on. As you just saw, the answer is hundreds of thousands of kilometers different!

The author says, "The only drawback of using a non-inertial frame of reference is that we have to append various pseudo-forces to the equations of motion." So he admits that the Coriolis force and the centrifugal force are pseudo-forces! And clearly it is not really a drawback to have to muck up the math like this, since that was the whole point. The math is being mucked up on purpose, to hide the fact that it is all completely unsupported. It is a hash. It is a fancier hash than the hash at Wiki, but it is still hash.

Yes, these samples of "full math" are always just misdirection. They are not posted to provide you with the full math. They are provided to prevent you from seeing the mechanics. They are provided to finesse some answer they desire from pages full of nonsense, making sure that no one can possibly follow the nonsense.

As for the Coriolis force, it is also a ghost here. Physically, there is no Coriolis force. It is not even a pseudo-force, it is only a curve caused by position. It is a simple outcome of pre-Einstein relativity and has absolutely nothing to do with the inertial or non-inertial field. That is why it only pops up in the so-called "non-inertial" math. That is to say, it is not dynamic or kinematic. It is fabulously easy to pick a frame of reference in which it doesn't play a part, so the choice by physicists to include it in any math should be a big red flag. Currently, it is only included as an excuse to fudge the math. MM has not seen any example where it was not used that way, and it is used that way here. (See MM's paper on Problems with General Relativity: Curved Space is Unnecessary and the Inertial System is Ignored and on his site the Coriolis effect where the merry-go-round is an example of the Coriolis effect.)

To see how far the current equations have been pushed, we just complete the math that was, or solve for zero using the first equation from the university pdf, as MM has copied above. We find that at 2.586 x 10⁵ km, the Earth's acceleration upon point 1 matches that of the Sun. That is a long way from the current Lagrange point.

Hmm. Let's write that out in the long way and study it. 258,600 km. That's in the same ballpark as the orbit of the Moon. Maybe the Moon really IS hitting the Lagrange points, or trying to. The Moon is inclined five degrees to the ecliptic, so it doesn't hit the right plane every month, but it isn't far away. And since the nodes travel, it will hit them occasionally. We know that from eclipses. At Solar eclipse, the Moon is nearest Lagrange point 1, one way or another, since it is right between Earth and Sun. So let's do the math using my unified field equations, instead of Newton's equations or Lagrange's. And let's do them following this idea: perhaps the Lagrange point is varying in practice because it depends on the charge of the object in question. If we solve for a mathematical point, for instance, that point will have no charge. In which case we will do a straight balance of solo gravity from Sun and Earth. But if we solve for a satellite like SOHO, we must remember that its charge, though small, is not zero. It cannot act like a point, therefore it will not go to the actual Lagrange point. It may go near it, but it will act a bit differently than a point. And if we take a large body like the Moon, with a large charge of its own, it will go to a Lagrange point many thousands of kilometers away from the Lagrange point proper. In other words, the Lagrange point or balancing point of 1) a point, 2) of SOHO, and 3) of the Moon may be very different.

Again, the math will be simple, because there are no centrifugal forces in my math. The centrifugal force was proposed as the equal-and-opposite reaction to the centripetal force, but my math, like Einstein's, contains no centripetal force. There is no string between here and the Sun, not even an abstract string or a mathematical string. Einstein's equations have no centrifugal force because he has no centripetal force. You cannot have a reaction to nothing. My equations do not contain a centrifugal force because MM has shown that neither the object nor the field contains one. Both logic and all data tell us that. A centrifugal force is a reaction of the body, not the field, so it is not included in field equations, ever. And it is not included in celestial field equations because the field is not created by a string between objects, or any other pull.

We will calculate for the Moon first. Since 384,400 km is about 60.27 Earth radii, we can see if the unified field balances there. But we have to put a real body there, not a point. We can't calculate charge for a point.

First, the math needs to be done. MM calculates the important accelerations due to the three bodies and the two fields. Once the gravity is separated from the charge in the unified field, gravity is shown to be only a function of radius. It is no longer a function of the inverse square. Unified, the two fields still follow the inverse square (roughly), but once separated, they don't. MM uses his new numbers for solo gravity, calculated by subtracting the charge field from the old gravity number. For instance, the current surface gravity of the Sun is said to be 274m/s², but in Magnetopause on MM's site we really have 1070 for solo gravity and -796 for charge, which sums to 274. The same applies to the Moon, so my number for the Moon, 2.668, is also not the current one. It is g/3.67 because solo gravity follows radius only. MM uses 9.7895 for g because that is the current number 9.78 + the number MM has found for the Earth's charge .009545. MM always uses equatorial numbers, because charge is heaviest at the equator. Besides that, we need one more correction to the field. In MM's unified field paper, he developes equations for a two-body problem. But here we have a three-body problem. This changes the charge math, since the charge of the two smaller bodies is in the greater field of the largest body. As MM showed in his papers on axial tilt and Bode's law, this directionalizes the main charge field. In other words, charge emitted toward the Sun acts differently than charge emitted away from it. Charge out drops by 1/r⁴, while charge in increases by the distance. MM shows that this is due to the field lines, whereby charge density increases as you go in and decreases as you go out. The field itself is already denser as you go in, as charge is channeled into the center, and this greatly affects all the charge math. Three-body problems are therefore completely different mathematically than two-body problems, since you have an ambient charge field already existing before any emission by the bodies. Of course without this knowledge, previous math could not hope to match the motions without huge amounts of pushing. The same math MM used in his paper's on Bode's law and axial tilt on MM's site, since that math is the simplest and most transparent as a matter of mechanics and vectors.

Staring with charge, it can be shown that charge is a function of both mass and density. Since we seek a charge density to work with, and since mass and charge are equivalent in the field equations, we seek a mass density. So to calculate relative charge (charge of one body relative to another), you multiply mass times density. This means that the Sun has 85,063 times as much charge as the Earth. Therefore, if we give the Earth a charge of 1, the Sun has a charge of 85,063. Since the Sun's charge is moving out from center, we take the fourth root.
⁴√85,063 = 17.078
But since the charge field of the Earth is actually .009545m/s², not 1, the actual charge field of the Sun is
17.078(.009545) = .16301m/s²
Since the Earth is 1/388 times as far away as the Sun, the Earth's relative charge at the Moon is only
.000025. To find the total charge field at the Moon, we add
eq.1 .16301 + .000025 = .163035m/s²

Now we do the gravity.
eq.2 Gravity from Earth to Moon 9.7895/60.27 = .162427
eq.3 Gravity from Moon to Earth 2.668/60.27 = .044267
eq.4 Gravity from Sun to Moon 1070/23,395 = .045736
eq.5 Gravity from Moon to Sun 2.668/23,395 = .000114

We add eqs.4 and 5, then subtract 3 from that, then subtract that from 2, to get .16084. Then we subtract that from eq.1, giving us .002195m/s². Since that is very close to my corrected number for the offset of the tangential velocity of the Moon (calculated in A Correction to Newton's Equation a=v²/r) of .002208m/s² (MM found that number instead of the current number .002725, by using 4 instead of π.), this appears to solve the problem.

Please notice that MM has solved this problem with five equations, composed of fractions and sums. Then remind yourself of the math string theory is throwing at this same problem. Yes, superstring theory is attempting to create a unified field. We are told that supercomputers are needed just to store the postulates and operations, and we are expected to be impressed by that. But the ones who used to trumpet elegance were correct. The right answer is always much simpler than we imagine. It is just difficult these days to imagine a simple answer. The waters have been so muddied by so many unclean swimmers thrashing about and by so many years of pollution being dumped indiscriminately into the river, a lonely bather cannot imagine looking down and seeing the bottom, even when his feet are firmly planted on it.

The only remaining disclarity in my math is the subtracting of the last numbers, instead of adding. It has seemed to some of my readers that the charge force of the Sun must be out, and the gravity of the Earth on the Moon, also out. MM has shown that charge is a bombardment of charge photons, therefore the Sun must push the Moon out. And the Earth also pulls the Moon out. Therefore, shouldn't we add them? No, although MM sees the fuzziness there. MM admits that it is sometimes beastly difficult to keep track of these field vectors. If it were easy, this problem wouldn't have sat unsolved for centuries. Again, the answer is that both the Moon and Earth are in the the greater field of the Sun. Therefore, as vectors, we can't just measure the Moon relative to the Earth. We have to measure both the Moon and Earth relative to the Sun. In other words, if we wanted to take the gravity vector of the Earth on the Moon as pointing out, we would have to take the Earth as a fixed point. But the Earth is not the fixed point in this field, the Sun is. Remember, the Earth also has an acceleration vector pointing at the Sun, although we have been able to ignore it in this math.

You will say, "But you just showed that the Earth's gravity is stronger than the Sun's in these equations. If the Sun's field is weaker at the Moon, then shouldn't the Earth define the gravity field there?" No. MM only showed that the Earth's apparent force at the distance of the Moon is greater than the Sun's, but of course MM did not show that the Earth's field is greater than the Sun's overall. That would be impossible, wouldn't it? The Sun's gravity field is the baseline field, and it therefore sets the direction of all the vectors. It doesn't matter that the Earth's "pull" is greater at a certain place in the field. What matters for the vectors is the baseline field, and the Sun's field is obviously the baseline field. Since the Sun's gravity is in vector opposition to the Earth's gravity in this position, it has the effect of flipping the vector. So, yes, it almost looks like the gravity of the Earth is pushing the Moon nearer the Sun. It isn't, but it does kind of look like that in the math, at a glance. [This is also why we add the charges in the first part.]

So MM has found that the Moon is at its own Lagrange point 1, given its velocity. MM has shown that all the accelerations and vectors balance, at a single position, without any difficult math. No Lagrangians, no Coriolis forces, no centrifugal forces, no pseudo-forces or pseudo-math. No curves. Just fractions. This has never been done before. The current and historical math only solves by integrating or summing, or by isolating forces. For example, we are currently taught that the orbital velocity of the Moon balances the centripetal force from the Earth. The centripetal force of the Earth at that distance is .002725, and that balances the Moon's velocity. Unfortunately, that leaves the Sun out of it. MM supposes we are expected to believe that the Sun's force is the same all around the Earth, and sums to zero or something, but that isn't borne out by a close examination of either Newton's field or Lagrange's.

Another thing to notice is that we only have to slow the Moon down a bit to make it hit a more tightly defined Lagrange point. Historically, the Lagrange point hasn't been stationary in the field, of course, since if the Earth is moving, the point has to move with it. We would drop the Moon's velocity from 31km/s to just under 30km/s, to make it stop orbiting. If we could slow it instantaneously right at that position, we might make it hover in eclipse, permanently. Of course there are other instabilities in a real problem, including the Solar Wind and charge from Venus and Jupiter, to name the largest, but we won't concern ourselves with that here.

What MM wants to do now is see if that Lagrange point is at the distance we found above, using Newton's simple equations. Remember that we found the number 258,600 for the Lagrange point, using Newton's math instead of Lagrange's. What if we put the Moon at that point with an Earth-shadowing velocity of 29.75km/s? Would it stay there, without orbiting the Earth (ignoring other instabilities)? No, if we run the numbers again, we find a repulsion of .101m/s², so we have gone way too close. What we find is that the correct distance for balance, with no orbit, is around 380,500km. We only have to move the Moon 3,500 km from its average orbital distance to achieve a non-orbiting balance at Lagrange point 1. Since that is already in the current range of the Moon, you can see that the forces that cause the Moon to orbit aren't very different from a non-orbiting balance. In other words, it wouldn't take much of a blow at eclipse to make the Moon hover in eclipse (or it wouldn't if the Moon were orbiting retrograde). We just slow it from about 31km/s to about 29.5km/s, relative to the Sun.

And so, the Moon's Lagrange point 1 is at about 380,500km. The Moon is where it is because it is staying near its Lagrange point, which completely contradicts current math and theory. However, it confirms logic. As MM said, we should have expected the Moon to hit its Lagrange point at Solar eclipse, since we know the Moon is in balance. If the Moon weren't in balance, it would fly off into space. In fact, some of the old guys like Euler and Lagrange did expect it. Some of them were surprised that the Moon didn't hit this balancing point at eclipse.

Now let us calculate the Lagrange point for a point. To do this is completely theoretical, since points don't exist, either in fields, in math, or in Nature. But if we want to understand how the current equations fail, we can correct them while staying as close to their postulates as is physically possible. A point will feel no charge, since charge is a collision. You can't collide with a point. Our point also can't have its own gravity, since a point can't have mass. And so our math is just that much simpler. We only need equations 2 and 4. We find the Lagrange point at 1.3565 million km.

eq.2 Gravity from Earth to point 9.7895/212.68 = .04603
eq.4 Gravity from Sun to point 1070/23,243 = .04603

This is closer to the current number, 1.5 million km, but that number is almost 10% off. Even when they try to match their math to real orbits, they still fail by 10%! You will say, "How can they be 10% wrong, when the satellites are there? Are you saying the satellites aren't there?" No, of course not. MM is saying that the satellites are neither points nor bodies with much charge, so they won't go to either the Lagrange point for a point or the Lagrange point for a Moon. To understand why they are near 1.5 million km with some degree of stability, you have to study the actual Halo orbit or Lissajous orbit that they are in. Both the Lissajous and Halo orbits act to make the orbiter seem bigger than it is in the field. So, in effect, what they have done is stretch out the radius of the "point", while keeping its mass and charge near zero. The less motion they gave to the satellite, and the smaller the satellite, the closer they could take it to the Lagrange point at 1.3565. But tiny satellites aren't useful, and tiny governors aren't either. It is much easier to let a satellite move, and govern its motion. That is why they use these pattern orbits.

Lissajous "orbit"

Anyway, if we start at my Lagrange point 1, and we expand the point by giving it both radius and mass, it will have charge also, and we will have to go closer to the Earth to keep the balance. The Sun will respond to the increasing charge, and will push it away. That is why the Moon is inside the Lagrange point proper. But if we increase the radius and don't increase the mass, we will have to go away from the Earth to keep the balance. The larger radius makes the Earth seem to push it away, as in the equations above. But the Sun does not respond in kind, because the charge hasn't increased. This is what is happening with our satellites that are supposed to be at Lagrange point 1. They are mimicking a larger object with a fast halo orbit or something, and the field takes them to be an object with the radius of the halo. But since the halo is empty, with no charge, the Sun does not respond in kind. The Lagrange point has seemed to move away from the Earth.

Now, MM has just claimed to have solved another 300 year old problem, but skeptics will say, "This is just a general solution to the 3-body problem, and we have had those since Newton. At the end of your math, you still miss by a fraction, so how can you claim to have bypassed chaos theory and perturbation theory? You would need to solve to fifty decimal places to do that, and you haven't even solved to six!" This critique completely misses the significance of what MM has just done. It was shown that the field equations were fundamentally in error, which means they weren't right at any decimal point. The equations added by Lagrange weren't a correction, extension, clarification, or even a fine-tune, they were only a complex mathematical push. To be specific, the current field equations are wrong because they can't insert the field numbers MM just inserted. For instance, they can't use the number 1,070 for the Sun because they have no way of calculating it, straight from first postulates. And they can't represent the degree of freedom in the charge field, because they don't understand there IS a charge field, much less that it changes in a different way out than in. They haven't got the right exponents; they don't have the plus and minus signs in the right place; they don't have the right two fields. And so their math is wrong. It is that simple. MM can make my numbers out better by using better numbers in; they can't. My error is just a matter of measurement, and of inserting more data. Their error is caused by faulty equations. There is a big difference. For this reason, MM does not need to solve to fifty decimal points. Using my new equations, any monkey can extend them into n-body problems or into real engineering problems. MM did not approach this problem or write this paper intending to solve down to the atom, MM intends to show and fix the unified field under the old equations, and MM has done that.

The Calculus Is Corrupt

The current and historical method for differentiating is a mess. In Lagrange's derivation of the virial on MM's site The Virial Theorem Is False, we find him differentiating x² with respect to t, to find 2xdx/dt. He then lets dx/dt equal v, so that dx²/dt is equal to 2xv. MM found this astonishing, but then was more astonished to find that it is done all the time, to this day. No one calls Lagrange on this cheat because they want to use it themselves. It is the same reason the Democrats never called the Republicans for stealing elections with voting machines. The Democrats wanted their turn with the machines, and got it.

We could continue this cheat of Lagrange to find that 2xv = 2x²/t, which would mean that the derivative of x² with respect to t is 2x²/t.

Does any of this make any sense? Does anyone ever bother to check to see if these equations are physically true? Apparently not.

If the derivative of x² with respect to t is 2xv, then what velocity is that? One will be told it is the velocity at (x,t), but 2x is already the velocity at (x,t). Because our power is 2 here, we have a curve equation. The derivative of a curve at a point is a velocity. It is supposed to be the instantaneous velocity at that point on the curve. The derivative is the tangent to the curve, remember, and it is also the velocity at that point. So by this finding of 2xv, we appear to have two simultaneous velocities at a single point, multiplied together. The value 2x is the velocity, and v is also the velocity, so we actually have v². The derivative of a power 2 curve equation is a velocity squared?

The derivative of x² with respect to t cannot be 2xv, since the derivative is the rate of change. The rate of change of x² with respect to t cannot be 2xv, unless v=1. Historically, Newton used the notation dx/dt (or the equivalent) here simply as a reminder of the relationship. It is like a listing of physical dimensions in an equation, not a continuation of variables. For example, if we find the derivative of x² with respect to x, we find 2x, which could be written 2x(dx/dx). That would be read, “The rate of change of x² is 2x(x with respect to x).” But since it is clear that dx/dx=1, we drop the notation.

When we find the derivative of x² with respect to t, we are doing the same thing. We can write that as 2x(dx/dt), but only if we remember that dx/dt is just notation. In that equation, dx/dt is reducible to 1, so it cannot be written later as a velocity variable.

In fact, in this notation, dx/dt IS the dimensional notation. It does not stand for a velocity variable, it stands for meters/second, or something like that. If we find the derivative of x² at x=4, the answer is 8, and the dx/dt only stands for the dimensions. We need dimensions, since 8 is not a physical answer. Since x² is an acceleration, the rate of change of that curve at a given x must be a velocity. The derivative of an acceleration is a velocity. So dx/dt is giving us the velocity dimensions of length over time. The ratio dx/dt is not a velocity variable, it is dimensional constant.

The ratio dx/dt is reducible to 1 simply because, physically, distance and time cannot be changing at different rates, as infinitesimals or at the limit. You will say that if our velocity is 2, our distance is changing at a rate of 2 while our time is changing at a rate of 1, but in the calculus, first order changes like that are ignored. The derivative of 2 is 0 and the derivative of 1 is 0. That is why the ratio in the notation is written dx/dt. It is not written x/t. The letter d here does not mean delta, it means fluxion or infinitesimal change. At the limit, all first order changes are equal, so dx/dt is vanishing in the same sense that 1 is vanishing in equations. It is vanishing in the sense that you can ignore it. You can cross it out of the equation. If you were Newton, you would think of it as a dot over a dot, and let it vanish for that reason. If you are with me, you think of this as 1/1, which is “vanishing” for a different but mostly equivalent reason.

That notation dx/dt here is not a representation of how x and t are changing relative to each other in any specific problem, it is a representation of how x and t are changing relative to each other in the physical field or space, absolutely. It is analogous to dx/dy. If we study space itself, does x change at a different rate than y? Do we measure the width of space differently than we measure the depth of space? Does space itself get wider faster than it gets longer? No. In physics, dx/dy always equals 1, just as dx/dx always equals 1. For the exact same reason, dx/dt always equals 1 in this sort of notation. Since time is defined relative to distance, they cannot be changing at different rates. If x is changing at a rate of 1, t must be changing at a rate of 1, and this has nothing to do with the velocity of any real object in any real measurement.

To show what is meant when to say that this notation is equivalent to dimensional notation, we can look at some common equation in physics. Say,

G = 6.67 x 10^-11 m³/kgs²

You can't rewrite that as

G = 6.67 x 10^-11 v²m/kg

And then start inserting different values for v into that equation. That second equation is true only in the case that v=1. v is not a variable there, it is just a dimensional analysis.

It is the same with the notation dx/dt. The ratio dx/dt can be written as a velocity only if you remember that v=1. In that case, v is not a variable, it is just a constant dimension, reminding us of a prior relationship. In Newton's and Leibniz's notation, they used dx/dt (or its equivalent) only in this way.

Therefore, Lagrange's math is just a cheat. Any time you see dx/dt written as a velocity, in a situation like this, a big red flag should pop up.

You will say, “C'mon, we all know that dx/dt is a velocity. What are you talking about? Velocity is defined as dx/dt, for heaven's sake!” Yes, in many situations, it is. MM is not denying that dx/dt is a velocity, as long as it is used correctly. What MM is denying is that dx/dt in this particular case is equivalent to the definitional notation of velocity. MM is pointing out something fundamental and of great importance, and you better open your eyes to it. The notation of calculus has always been convoluted and sloppy, and this sloppiness had already reached epidemic proportions by the time of Lagrange. If you differentiate x², finding 2xdx/dt, the dx/dt in that notation is not a velocity. The notation is telling us that we are finding the rate of change of x² with respect to the given rate of change of time. Since the given rate of change of time is always 1, dx/dt must also be one.

To put it another way: in physics, time never changes its rate. Time itself cannot be accelerated or dilated, not even in Relativity. In Relativity, measurements of time can be dilated or compressed, but time itself is invariable. We never find time to any power. We never find time going at any rate above 1 or below 1. Time is always ticking at a rate of 1, by definition. The rate of change of time is and must be 1. Therefore, if we are given the ratio dx/dt, and we know that dx is 1, then dx/dt must be 1. Well, if we differentiate some power of x with respect to t, then dx can hardly be anything but 1, can it? Given x², we assume dx=1. If we differentiate x² with respect to x, we assume dx=1, don't we? If we didn't, then we couldn't find that dx²/dx=2x. The denominator dx has to equal 1 or the equality is ruined. In the same way, when we differentiate with respect to t, dx is still changing at a rate of 1. Therefore, dx/dt=1. It can be dropped.

If we differentiate x² with respect to t, the answer is 2x, not 2xdx/dt. This sloppy and confusing notation should be abandoned. The ratio dx/dt should mean one thing in calculus and one thing only. It should not be used differently in different places, since that only encourages this sort of cheating.

MM has also seen x² differentiated with respect to t to get 2xx'. That is unnecessary for the same reason. It just gives cheaters another variable to play with, to fudge later if they want. The term x' just means the derivative of x, and of course the derivative of x is just 1. So there is no reason to write it. The only reason to write it is so that you can use the Lagrange fudge later, claiming that x' = v, and push your equations that way. MM has seen “real” mathematicians defending this manipulation, claiming that whenever you differentiate a length, you get a velocity. But that is the upside-down calculus in A Study of Variable Acceleration. Many mathematicians and physicists actually believe they can differentiate any length they like into a velocity. But they cannot as MM has shown with Lagrange and his virial proof. They have to be given an acceleration, and every length is not part of an acceleration. Because they have misunderstood calculus from day one in high-school, they think that when they differentiate some power like x², they are differentiating a length. But they aren't. When you differentiate x², you are differentiating a curve, which is an acceleration. The term x² is already an acceleration, even without a ratio, a denominator, or a “with respect to.” The term x² stands for this accelerating series of numbers:

x² : 1, 4, 9, 16, 25, 36, 49, 64, 81

Therefore, you differentiate an acceleration into a velocity. You do not differentiate a length into a velocity. You differentiate down, not up.

But as it is, mathematicians think they can differentiate both up and down. They can differentiate x² into a velocity, because 2x is a velocity at the point x; and they can also differentiate x into a velocity, since x' = v. But their second manipulation here is illegal, since they have just differentiated up, with no given acceleration or curve. If you are given x, you are not given a curve or any variable change. You are given this series of numbers:

x : 1, 2, 3, 4, 5, 6, 7, 8

The derivative of that series of numbers is 1, because the rate of change of that line is 1. There is a difference of 1 between each and every term. If you assign a velocity to that series, it is also 1. You cannot differentiate x into a velocity variable. You can only differentiate x into the velocity 1.