Problems with General Relativity:
Curved Space is Unnecessary
and the Inertial System is Ignored

Curved Space is Unnecessary

First written November 2004

Relativity has been an important historical step in physics, and this is generally understood, even by non-physicists. Einstein has become one of the most famous people in history due to his contributions to physics, and in many ways he deserves this fame. Although Relativity as he presented it was flawed in any number of ways, and although his method of presentation has caused untold confusion, he is responsible for several real advances. He gave us the first formal theory and math to contain the finite speed of light and many of its implications. He convinced the world of length contraction, time dilation, mass increase, and mass-energy conversion, and supplied us with transforms for all these phenomena that were very close to correct.

All this being said, it is nonetheless shocking to discover the magnitude of some of his errors. Even more shocking is that these very simple algebraic errors have stood for a hundred years under the noses of many famous mathematicians and physicists. In the paper An Algebraic Correction to Special Relativity and Refutation of Gamma Miles Mathis has shown incontestably that the first derivation of gamma is riddled with errors of high-school level algebra, and yet this derivation has never once been corrected or even seriously critiqued. Mathematicians of the first rank, including Russell, Minkowski, Dirac, and Feynman have left it untouched. Since Relativity is math applied to a very complex problem, it is perhaps not surprising that pure mathematicians have not fully penetrated its physical side; but that “towering” mathematical physicists like Bohr, Dirac, Feynman, and many others could not see the errors is astonishing, to say the very least.

MM's critique of Special Relativity has so far ignored the tensor calculus. Since the space of Special Relativity is flat to begin with, the tensor calculus is not necessary. A Gaussian co-ordinate system is an intrusion in SR. That is why Einstein initially derived his transforms without it. That he could do so is clear—his algebraic derivation is uncorrected by importing the tensor calculus into SR. The tensor calculus does not even fine-tune SR, it only expresses it in a different way. Gamma is the same transform with or without the tensor calculus.

The problem is that Einstein imported the tensors into SR very early in the history of his theory. He did this to impress the top physicists and mathematicians. It worked. But it also had the unfortunate side-effect of cloaking the fundamental level of the theory. SR was only a few years old when the time variable was swallowed up by hyperbolic math. Once that happened, no one cared to look at the old algebra anymore. It was much more fun to play with the new tensors, and top-level scientists and mathematicians of the time would not have been caught dead talking about Relativity in terms of classical variables. They wanted to be heard talking about covariant four-vectors and contravariant tensors of the second rank and Hamiltonians and so on.

Relativity has been buried under the tensors ever since. To this day, no one who thinks much of himself or herself will be caught discussing Relativity without using all the mathematical names and niceties. The tensor calculus is the insider lingo of Relativity, the secret handshake, the esoteric knowledge, the badge of honor.

This social fact has been and remains the number one impediment to improving Relativity. Einstein managed to create a very exclusive club, one that has become frozen in its forms of initiation and its bylaws. The tensor calculus by itself has provided the long apprenticeship, and this apprenticeship has allowed a sort of indoctrination. The years it takes to learn the math become a bridge that no one wants to look back beyond. The past is on the distant shore, and the new master is only interested in the future. Algebra is beneath him, a child’s toy. What is wanted is an ever more complex math with which he can preen himself and fill blackboards.

As an example of this, look at Paul Dirac's lead-in to the tensor calculus in his book General Theory of Relativity [1975]. He says,

One can easily imagine a curved two-dimensional space immersed in Euclidean three-dimensional space. In the same way, one can have a curved four-dimensional space immersed in a flat space of a larger number of dimensions. Such a curved space is called a Riemann space. A small region of it is approximately flat. (Section 5, paragraph 1)

That is his entire explanation of curved space. Afterwards he simply dives into the math. But his foundation is already cracked. First of all, a “curved two-dimensional space” is not two-dimensional. A curved two-dimensional space is three-dimensional, by definition. This mistake should already be a clue that Dirac is long on math and short on conceptual understanding and rigor. And it means that a curved four-dimensional space must be five-dimensional, in which case we need a variable and a variable assignment for this fifth dimension. We get neither from Dirac, and we have never gotten either from anyone else, including Einstein and Kaluza (Kaluza gave us the fifth variable but no assignment of it to any physical or temporal extension). Furthermore, Dirac's last sentence is necessary because he will use the calculus to do math in infinitesimal regions of Riemann space. But you can see that this is a sort of cheat: the mathematician postulates curvature and then ignores it by going to a tiny area where there is no curvature. This fact will be returned to later on.

To analyze the theory of General Relativity requires an understanding both the math and the theory of the math. Besides analyzing the postulates and physical applications of GR, one must also analyze the tensor calculus because in many ways, GR is the tensor calculus.

Analysis of the thought problems that led Einstein into his theory of General Relativity in the same order that he did.

In The Foundation of the Theory of General Relativity, published in Annalen der Physik in 1916, and the book Relativity, published the same year, Einstein tells the two famous tales as thought problems:

The first is of the elevator car in space: The elevator car in space showed the equivalence of gravity and acceleration. Einstein showed that without further information it was impossible to decide if an accelerating elevator car was in a gravitational field or not. The vector was theoretically reversible in all ways. In MM's opinion, this thought problem is brilliantly imagined and brilliantly stated. MM agrees with this, but believes that Einstein fails to take it to its logical conclusion.

The second is the spinning disk. Einstein gives us a spinning disk, like a merry-go-round, and then does thought transformations on it, to show the affect on measuring rods and clocks. An observer off the disk will see and measure things differently than an observer on the disk. MM agrees with this, but his list of observed changes is very faulty.

To begin with, Einstein says that the motion of the disk creates a sort of gravitational field. He says that the observer on the disk could make the claim that he was not moving, saying only that he was feeling forces from a gravitational field. The observer on the disk would feel a force outward from the center of the disk—the centrifugal force—and that the space-distribution of this "gravitational field" would be impossible according to Newton. In a footnote, he says that it would be impossible since, "The field disappears at the center of the disk and increases outward proportionally to the distance from the center as we proceed outwards."

Supposedly, he means that it would require the force of some massive torus surrounding the disk to explain the field as a gravitational one, and that Newton did not have much use for such things. But of course the reason Newton did not have much use for such things is that none had ever been discovered. No such thing has been discovered since the time of Newton, and so Einstein's footnote is a bit ridiculous. Newton's equations did not forbid the existence of tori, and Einstein's point is strange. Newton's answer to the observer who claimed to be in the field of a torus would have been, "show me the torus."

Notice that the torus would have to be in synchronous orbit around the disk as well, or the observer would see himself moving with regard to it (in which case he could not say he was not moving). If the torus was not in synchronous orbit, the observer could say that it was orbiting him. But in that case he would have to explain why he was feeling no effects from the spinning electromagnetic field of the torus.

More importantly, what Einstein fails to recognize in his example is that an observer riding upon such a disk would be feeling two forces, not one. If he was not flying off into space, he would necessarily be feeling a force of friction, which kept him on the disk despite the centrifugal force. This frictional force would be the one that is analogous to a gravitational field, since the frictional "field" is arrayed around a central point. This would indeed increase with distance, and for that reason alone could not be called gravitational. Gravitational fields, even those of Einstein, diminish with distance.

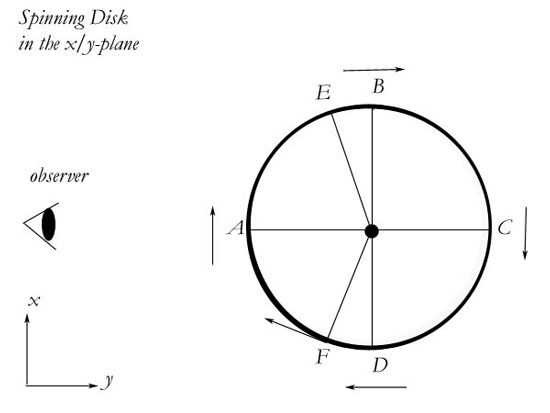
All that was admittedly inconsequential compared to what follows. For Einstein now begins his calculations. He says that if we place a clock on the edge of the disk and a clock at the center, then climb off and let the thing spin, we will see (from off the disk) the clock on the edge go at a rate that is permanently slower than the other. This is simply false. For one thing, you must pick a point of view. "Off the disk" is not precise enough. The differences will vary depending on where you position yourself relative to the direction of spin. For instance, one can pick a point where there is no difference in the two clocks. If you let the disk spin in the xy-plane, then draw the z-axis up or down from the center, you can sit anywhere on that axis —no matter how far away—and the two clocks will have the same rate for you. If the disk is very large, then the two clocks will not match up—meaning that the one from the edge will flash the time just a bit later than the one at the center. But this is only because you are closer to the center than to the edge. The periods of the two clocks will be exactly the same. If you are x distance from the edge, then the tick of the clock will be x/c late each tick. But if it is late the same amount each time, then the period has not changed.

Now, what if you are in the xy-plane, like the disk, but you are off the disk? This seems to be how most people imagine Einstein's example. Einstein's explanation is still wrong, as MM has proved in An Algebraic Correction to Special Relativity and Refutation of Gamma that approaching objects are not time-dilated, but time-compressed. That is, speeded up. The simplest way to see this is to think of the clocks as waves and then apply the Doppler Effect to them. Receding clocks are red-shifted, approaching clocks are blue-shifted. Therefore, let us say that the edge of the disk that is furthest to your right (D) is moving toward you, and the edge to the furthest left (B) is moving away. The first clock will be speeded up, the second dilated. The clocks at A and C will both be normal—no difference from your clock or from each other. If the disk is very large and C is very far away, then that time will appear late, but it will not be dilated or compressed. The effects on measuring rods will be analogous. D will look longer, B shorter, A and C will look the same. For this reason, you will not calculate the disk to be a circle. The distance ABC will look shorter than ADC. Points E and F will seem the fastest points to you, since at E the clock is moving directly away from you and at F the clock is moving directly toward you. We could graph a lot of points and draw the blob, but it is not that compelling beyond the points that have enumerated. It would look like a blob whose center of area would seem to have shifted forward and to the right, like an egg with its point out from F.

It is clear that this contradicts Einstein in regard to point D. It is less clear concerning points A and C and thus contradicts his SR analysis of the situation, an analysis he begins his GR paper with. He erroneously expects all moving points to be time dilated and length contracted, but in equation 71a of The Foundation of the Theory of General Relativity he finds that "with the tangential position, therefore, the gravitational field of the point of mass has no influence on the length of a rod."

It is hard to know what to make of this. On the one hand, his gravitational field is not spinning in eq. 71a. On the other hand, Einstein uses the spin in his disk example to create the pseudo-gravitational field. If the disk is not spinning, there is no field. Einstein does not solve this conundrum himself, since he never goes back to the spinning disk to apply his new theory to it.

Does General Relativity trump Special Relativity here, or will a spinning gravitational field cause tangential length contraction? Einstein does not say, since he never fully differentiates between his elevator car example and his disk example. He uses them both as lead-ins but does not really solve them. He implies that GR solves them both in the same way, but it should be clear that the disk problem introduces some subtleties that the elevator car, and a non-spinning gravitational field, do not.

MM's correction to Special Relativity allows for an easy solution to this problem without any tensors. MM agrees with equation 71a: General Relativity cannot be responsible for any effects at the tangent, whether that tangent is tangent to a gravitational field or to a spinning disk. In the paper An Algebraic Correction to Special Relativity and Refutation of Gamma MM included a special section on motion at a tangent, and there it is clear that the point on the tangent cannot be dilated or compressed, whether it is moving or not, since it is perpendicular to the line of sight. However, this brings up a further question. Only if the time period or rod length in question is very small will it be unaffected by the experimental situation above. A longer rod or a longer time period will in fact be changed in subtle ways. MM's claim above, that no dilation or compression will be seen or measured, is true only if the center of the rod or time period is at point A or C. In that case, if we have a rather long rod, then the "half" that is before C will be slightly shorter and the half that is after C will be slightly longer. This is because a y-component of the first half of the rod will be fleeing the observer, and the y-component of the second half will be approaching. The same, in reverse, applies to the time period.

However, if you have a rather long time period that starts at point A or C, then it must be compressed or dilated, since as it moves away from A or C it will develop a y-component relative to the observer. This y-component will be affected, and it will be affected more the longer it continues beyond point A or C.

It is also worth noting that all these rods will be not only stretched or compressed, they will also be curved. The y-components and x-components of the stretching or compressing will not be proportional, so that the rods will look bent from off the disk.

Having cleared up that subtlety, let us move on. Einstein’s main point is true that the circle described by the disk in its own field will not act like a circle if measured or viewed from outside that field since the observer will not see a circle. Therefore we require transforms.

So far MM's only disagreement is with Einstein’s analysis of specific changes in the fields, but now we must look at one of his main claims regarding the motion of objects, or of light, in accelerated fields. At the end of section 2 of The Foundation of the Theory of General Relativity, Einstein says this: “The path of a ray of light with respect to K’ must in general be curvilinear, if with respect to K light is propagated in a straight line with a definite constant velocity.”

He came to this conclusion via the disk example. All points on the disk are feeling a centripetal acceleration; therefore they are in a sort of gravitational field. Now, if we turn the disk into a merry-go-round and put a child on a horse on the periphery somewhere, and let that child throw a ball to the stationary observer, then the observer sees the trajectory as a straight line. The child sees the trajectory as a curve. The same basic analysis applies to the elevator car in space.

However, there is one subtlety of this problem that Einstein has missed. Both the child on the horse and the man in the elevator car are in real motion relative to the observer and to the field itself. To see what this means, let us look at the man in the elevator car. He is either in an elevator car that is accelerating upwards or is at rest in a gravitational field centered below him. If he is accelerating upward then he will see light (and all other objects that move in straight lines external to his car) as curved. But if he is at rest, then we must ask why he is not falling toward the center of the field. The bottom of the car must be supported by some solid structure.

If so, then we must change his description: he is either feeling one constant force up, or he is feeling two constant and equal forces, one up and one down. What he is not feeling is one constant force down. If he were feeling one constant force down, he would be moving in that direction. This constant force down would be the force of the gravitational field acting alone, without any structure to resist it. We know he is not in this situation because if he were he would not be stuck to the floor of the elevator car. Einstein says that he is stuck to the floor. If he and the elevator car were in freefall, then he would be floating just above the floor of the car.

The problem is that this last situation is the only one that GR finds equations for. GR calculates accelerations at different points in the field. But Einstein’s elevator car does not fit this situation. It is not falling freely in a field. It is at rest in a gravitational field. This is important because a body at rest in gravitational field and a body falling freely in a gravitational field do not see light in the same way. A body falling freely is accelerating, and therefore Einstein is correct to say that it would see light traveling in a curve. But a body at rest in a gravitational field would also be at rest relative to any external field. Therefore it would not see light travel in a curve.

This means that Einstein’s quote above is false. It would be true only if it read, "The path of a ray of light with respect to a body accelerating in K' must in general be curvilinear, if with respect to a body in K light is propagated in a straight line with a definite constant velocity." This is because, if a person is standing on the earth and the earth is K’, she may be feeling a force of gravity, but she is not accelerating due to that force. If she is not moving with regard to K’ and K’ is not moving with regard to K, then she is not moving with regard to K. There is no reason for her to see incoming light as curved. She would see incoming light as curved only if she were in freefall.

This is a critical error for Einstein, since he uses the sentence above to justify all kinds of things. He treats it as proved and then considers it an axiom. A false axiom of this magnitude is difficult to overcome without a lot of mathematical tricks. Unfortunately, as MM will show, the tensor calculus provides Einstein and others with a nearly bottomless bag of tricks.

Einstein's next step is to ditch Euclidean space in favor of
Gaussian co-ordinates and the tensor calculus

There does not appear to be any good argument for doing so in any of his writings. Gauss' method only works if "sufficiently small areas under consideration act as Euclidean areas," as Einstein admits. This must be considered in itself a theoretical reductio since the Gaussian method is a method of infinitesimals, and the field must be considered Euclidean at the infinitesimal level. If this is true, then the method cannot be said to apply to non-Euclidean systems, except as a kind of fudge.

Nor is it clear why it is necessary that the gravitational field be non-Euclidean in the first place. Einstein's examples of the elevator car and disk do not lead in that direction, although he implies that they do. He says "it is not possible to obtain a reasonable definition of time," with regard to the disk or any other gravitational system using flat fields.

However, a reasonable definition of time can easily be offered with regard to any system. A rotating system is no different than any other system. There transformation equations are quite easy to come by (although the equations increase in number), and can offer a definition of simultaneity as well. Just as MM showed with Special Relativity, some observers will be privileged, by utilitarian considerations which can be proven once again by Doppler shifts.

Furthermore, the tensor calculus introduces a margin of error into all calculations, as shown by Einstein's inclusion of Appendix II in The Meaning of Relativity. Although this imprecision is more widely known as the "strength" of various field equations (depending on the "free data" in the system), in MM's opinion this imprecision or margin of error is just that. It is caused by treating the field as non-Euclidean and then applying infinitesimal Euclidean math to it. Since gravity is believed to be a force acting over large distances, and is treated by General Relativity as such, it is absurd to apply to it a math that only works well in small sub-areas—areas where gravity is not even applicable.

In section 4 of The Foundation of the Theory of General Relativity, Einstein says, "For infinitely small four-dimensional regions the theory of relativity in the restricted sense is appropriate, if the coordinates are suitably chosen." This means that SR applies at the limit, and that the gravitational field becomes flat at the limit. But of course if the field is flat or rectilinear at the limit, then the gravitational field does not exist at the limit. It is difficult to see how we are going to find equations for the gravitational field by going to a limit where it does not exist.

This is where we must look very closely at the fundamental assumptions of the tensor calculus. In A Redefinition of the Derivative MM has shown that the regular calculus has historically proceeded by a compensation of errors and by following the diminishing differential instead of the constant differential. The tensor calculus followed Newton in assuming that a curve could be straightened out by making it appropriately tiny. Einstein had no reason to question this assumption. But in fact, it is a false assumption, both for the regular calculus and the tensor calculus. The derivative equation is derived not from going to a limit but from going to a sub-interval. The derivative is not a variable at an ultimate or infinitesimal interval. It is the change in that variable over a subinterval of 1.

Now, it is true that the tensor calculus mostly works, and it mostly works for the same reason the regular calculus mostly works: the derivative equation, although wrongly derived, is a correct equation. It gives us the right numbers. But the tensor calculus is conceptually sloppy in exactly the same ways as the regular calculus, and then some. For example, the regular calculus has taken a lot of heat historically for sometimes treating the variables at the limit as zero and sometimes treating them as very small quantities. The tensor calculus does the same thing. Let’s look at Einstein’s derivation of his fundamental tensor. He starts with this equation:
ds² = -dx₁² – dx₂² – dx₃² + dx₄²
This is the famous four-vector equation he inherited from Minkowski. Obviously, none of these vectors can be zero. They are only very small. In fact, they must not be zero. If ds is zero, then we cannot calculate solutions.

Some pages on, at the beginning of section 8, we get this equation:
ds² = g_μν dx_μ dx_ν

Once again, these infinitesimals cannot be zero. They must not be. But in equation 18a of section 8, Einstein gives us this:
dτ₀ = √-g(dτ)

Where τ is the volume. And says, "If √-g were to vanish at a point of the four-dimensional continuum, it would mean that at this point an infinitely small 'natural' volume would correspond to a finite volume in the co-ordinates. Let us assume this is never the case, then g cannot change sign….It always has a finite value." This means that the infinitesimal values must be zero. If they have no finite value then they must be zero. There is no third choice.

Even Newton and Cauchy understood this. The epsilon delta proof understands it. Newton said, in effect, "any value you can name, I can name a smaller one: that is all that is necessary to this proof. My value is smaller than yours but it is not zero." The epsilon delta proof mirrors this argument with a bit more rigor. And yet the tensor calculus and Einstein proceed by disallowing the volume at the limit from having any finite value.

In one place in the proof ds must not be zero, at another dτ must be zero. The tensor calculus, just like the regular calculus, cannot decide whether the infinitesimals have extension or not. They must have extension in the math, they must not have extension in the physical field.

Another thing is curious here that cannot be passed without a comment. The very next equation in Einstein’s text is this one:
Eq.19: |dx’_σ/dx_μ| = 1

This is found by letting √-g = 1, so that dτ’ = dτ. This is extraordinary, because if the volume of every infinitesimal is equal at the limit, then that means that everything is equal at the limit. Time and distance must be equal at the limit, which means that space is homogeneous at the limit. Not only is the field rectilinear at the four-vector limit, it is non-time-dilated and non-length-contracted and non-mass-increased. Einstein admitted above that SR works at the GR limit, meaning that the field is Galilean and Euclidean at that level. But he has not taken his analysis far enough. Volumes are not equivalent in SR, since lengths are not equivalent. Therefore his GR field at the limit must be an absolute. He almost admits this when he says, “The invariant √-g(dτ) is equal to the magnitude of the four-dimensional element of volume in the ‘local’ system of reference”.

Einstein's word “local” must mean the local system, which is the system measured locally, from no distance. Feynman also makes use of the local system in trying to explain some of the subtleties of Relativity. By using the two words “local” and “invariant” in the same sentence, Einstein has come as near as he ever did to the word “absolute”. He might as well have admitted it: according to the tensor calculus space is absolute at the limit. Meaning that it is invariant in every way. All local time and distance is equivalent, invariant, and absolutely equal to all other local time and distance.

MM does agree with his math, but he agree with Einstein's postulate: all local time and distance must be equal in order to measure relative differences. If you do not postulate local invariance you cannot derive transforms at all, neither in SR nor in GR. Of course this is extraordinary because it contradicts the current interpretation of Einstein, which insists that the local field does not exist. The standard interpretation likes to believe that Einstein somehow derived his transforms from nothing. It likes to insist that Relativity has no absolute postulates, except for the speed of light. It likes to insist that there is no absolute space, even at the limit, since this would seem to imply an ether. Nothing is more passé than the ether. MM is not arguing for the reinstatement of the ether, but it is clear that we must postulate the equivalence of all local time and space. It seems clear that Einstein admits this, in his own way, precisely here. In An Algebraic Correction to Special Relativity - Part VIII: Conclusion MM has shown that the reason this must be true is that making the speed of light absolute determines, by itself, that the local field must also be absolute. The two postulates are equivalent. If you assume that light is a constant, you must also assume that dt and dx are constants. That is to say, the local field is invariant. The speed of light is a clock setter. It is also a length setter.

Solving a GR problem without tensor calculus to show it is superfluous

The first problem Einstein solves with his new math and theory is the refraction or aberration of starlight by the sun. He has already posed as an axiom the fact that light moves curvilinearly in a gravitational field. Now he only needs to calculate the amount of curvature in a real field. (See The Aberration of Starlight is an Expanding Earth)

There MM calculates in a completely different way. MM dismisses Einstein's axiom as unproved. MM does not accept that light must travel curvilinearly in a gravitational field, except under certain conditions. It will appear to travel curvilinearly to an observer in freefall or in orbit. We here on earth observing starlight passing the Sun are in a sort of freefall relative to the gravitational field of the Sun, so we would see starlight curve. But in this case, it is the acceleration of the Earth that makes the light appear to bend, not the pull of the Sun on the light. If you could stand on the Sun without burning up, you would be at rest relative to the central field and would not see starlight curve. The curvature of starlight is relative to position. It is not absolute, even within the field. It cannot be treated as an axiom. Therefore MM must solve in a completely different way.

To develop MM's method, we must return for a moment to the problem of the disk. Let the disk again be a merry-go-round, and let a child be on a horse on the periphery of the spinning ride. This child wants to throw me a ball. He can easily do so, and the observer will see the trajectory as a straight line, but the child will see the trajectory as a curve, provided he defines himself as stationary. This is all that Einstein means, or can mean. Replace the ball with a photon, and the child calculates that it has taken a curved path. But, once again, observer will calculate that it has arrived at my eye in a straight line.

Obviously we have two choices in developing transformation equations here. From the point of the view of the child, we need a math that describes curved lines. From the point of view of the parent standing off the ride, we don't. We can use pretty simple math. But once a transform is arrived at, it will work in both directions. All we have to do is reverse it. So of course we should choose to develop the transforms from the point of view of the parent.

Einstein claims that this is not always possible. There is not always a point of view that can be found where the paths of the light rays are straight. He gives as an example the gravitational field of the sun. There is nowhere one can go, he says, where one can calculate with straight light paths; therefore we need a new highly complex math. But this is simply not true. One may or may not be able to carry oneself physically to a place in space where the light rays passing the sun will appear straight, but one can easily carry oneself there conceptually. Just imagine that the sun is expanding at a constant rate, one that would perfectly offset the curvature of the light path. Then develop the transforms, and afterwards reverse the direction of the acceleration. You can do simple Euclidean math, meaning algebra, to describe the field, and then reverse it. You make all the acceleration vectors point toward the sun, instead of away from it. The field itself is exactly the same either way. If I am accelerating toward you, you are accelerating toward me. This obviates the need for curvilinear math altogether. And Einstein's own equivalence principle is what gives us permission to do this!

Besides, the reason we cannot carry ourselves physically to a point where light does not curve relative to the field of the Sun is an experimental reason, not a theoretical reason. Meaning that if we could bear very high temperatures, we could go stand on the Sun and see light without curvature. In fact, in a slightly different case, we could actually do the measurement. Einstein calculates a bending of starlight by Jupiter, predicting .02 arc seconds. Well, we could land on Jupiter and see the light unbent by Jupiter’s field there. On the surface of Jupiter, we would be at rest relative to Jupiter’s gravitational field. We would not expect to see a bend of .02 seconds of arc from that position.

Just think of the operator of the merry-go-round. If he were standing in the very center, and if he were not rotating, then he would not see the ball thrown off the ride as curved. He would see like the parents, not like the child.

Even from the point of view of the child on the merry-go-round, there is no need for tensors. Einstein says that Euclidean math cannot be used since no Euclidean space can be found in a gravitational field from which to measure the curvature. There is no orthogonal space underlying the curved space. But this is simply false. It is false since curvature necessarily implies a relation to a non-curved background. The meaning of curvature is absolutely dependent upon the existence of a straight line. If the child on the merry-go-round sees a ball thrown off the ride—or calculates a photon emitted—to travel a curved path, he must see it with regard to a Euclidean background. That background is in fact the "space" of the parent off the ride. If the space of the parent were also curved, then the child could not see any curvature. Motion, whether linear or curved, is always defined relative to a background. A curve in curved space is not a curve.

As proof of this, we know that starlight is refracted only by referring it to some Euclidean system. It is curved relative to the background we apply to it in order to see how curved it is. If the ray is refracted some measurable quantity, we know this quantity only by referring it to the path the light would have taken if the field of the sun were not present. This reference field of measurement is precisely the Euclidean field MM is talking about. Whether it exists in reality is not pertinent. It can be made to exist as a concept, and indeed it must be in order to measure the degree of aberration of starlight. This field is the field we should choose to do our math in, since it is a Euclidean field and requires no esoteric tensors or slipshod concepts. In fact, the curvature of the light defines the field at that radius. Since a gravitational field is not dependent upon the mass of the test particle, a photon will do as well as any other test mass. But again, the curvature or strength of the field could never be measured without referring it to the path a light ray would have taken without the gravitational tug. That is, a straight light path. This straight light path is precisely the orthogonal field we require: it is the Euclidean space underlying every non-Euclidean field.

In The Aberration of Starlight is an Expanding Earth), MM has proved this beyond a doubt where he finds the same number for aberration near the sun as Einstein, using only one simple algebraic equation. In comparison, let us look first at Einstein’s math. In 1911, he provided this equation in his paper On the Influence of Gravitation on the Propagation of Light:
a = (1/c²)∫(kM/r²)(cosθds)

where a is the aberration and the integral is taken from θ = π/2 to θ = -π/2.
This equation took him pages of complex math and theory to derive. Unfortunately, it gave him .83 arc seconds, a number that history has conveniently forgotten.

In 1916, in The Foundation of the General Theory of Relativity, Einstein gave us this equation [eq. 74]:
B = ∫(∂γ/∂x₁)(dx₂)

Where B is the aberration, the integral is taken from +∞ to -∞, and
γ = √(-g₄₄/g₂₂)

So we have an integral of partial derivatives, one of which is the transform gamma expressed as the square root of the negative ratio of two tensors. This equation took him 50 pages of math and theory to derive. From all this Einstein gets the number 1.7 arc seconds.

MM gets the same number from this equation:
θ = tan^-1(gt²/2)/d

Where g is the acceleration of the earth and d is the distance to the sun. MM derived this equation simply by turning all the acceleration vectors due to gravity around. Rather than have the acceleration vector g point at the center of the earth, MM turned it around and had it point from the center of the earth outward. Conceptually, this had the effect of making the earth actually accelerate spherically. Mathematically, it had no effect at all beyond flattening out the field. Turning the acceleration vector around made the field a Euclidean field, a field MM could do simple math in. Once MM achieved the number for aberration, he could leave the vector turned or put it back to the way it was. If he puts it back the way it was, it will return to a curved field, but the number is the same either way. Just look:

opposite = s = gt²/2
t = time for light to travel from the tangent of the sun to the earth
    = light time from sun to earth + light time of the radius of the sun
s = (9.78 m/s²)(501s)²]/2
s = 1,230,000m
tanθ = opposite/adjacent
tanθ = 1,230,000m/1.51 x 10¹¹m
θ = 1.68 seconds of arc

To see why this number does not match the current number 1.75, More Problems with General Relativity. There MM shows that gamma causes the current equations to fail. The number 1.75 is an outcome of the current equations, not of the newest measurements.

You will say that MM has ignored the gravity vector of the sun here, which is the main vector. But in the aberration solution showed that the operation of measuring aberration allowed us to ignore the sun’s field. If we turn the sun’s vector around in the same way we did the earth’s, then the sun will be expanding after the light has already passed the tangent. We do not care what happened before the light reached the sun, since the aberration did not take place then. We care what happened after the light reached the sun. But if we have turned the vector around in order to flatten out the field, then the expansion of the sun cannot affect the light. It seems odd, but it is the field of the earth that causes aberration, once the vectors are reversed.

You tell me which equation you would rather teach to students, or supply a full derivation for, or develop a theory to contain. The so-called free data in Einstein’s equations is considerable. There isn’t a speck of free data in MM's equation. MM's “field strength” is 100%.

No doubt you will say you would prefer to teach an equation that is correct. But MM's equation is correct. It gets the right number. Modern mathematicians have been famous for claiming that you can apply any math you want to a problem, as long as you do it in the right way. And they are correct. Minkowski answered his critics by saying that his fields were a mathematical convenience: he did not need to prove their physical reality, he only needed to get the right answer. In this, he was right. Any math that does not contain false postulates is as good as any other math.

(Minkowski’s math contains several false postulates, as shown elsewhere. It contains the false postulates of Einstein (like x = ct) and it adds to them the false postulate that time travels at a right angle to x, y, z. See Perihelion Precession of Mercury Explained)

But modern mathematicians have used this as an excuse for test-driving all sorts of esoteric maths. MM has turned the tables on them by showing a simple algebraic solution, in a Euclidean field, that undercuts their tensor calculus.

MM has achieved the ability to calculate in Euclidean fields by making a single change: turning all acceleration vectors around, simply reversing them. Einstein himself gave me the ability to do this. MM is not contradicting his theory, just interpreting it in simpler language and math. The vector reversal is a direct outcome of the equivalence he spent so much time proving. His elevator car in space showed us that mathematically there is no difference between “gravity down” and “acceleration up.” If this is true, then there is nothing stopping us from assuming the earth is accelerating up. We assume it just to do our math and then drop the assumption afterwards if we like. It is a mathematical convenience and nothing more, precisely like the convenience of i (except that MM's simple math is a lot more convenient than i). This is what “equivalence” means: it means that the two situations give us the same number. In developing equations, we are seeking numbers, nothing more. We can house those equations later in any theory we like. If “gravity down” and “acceleration up” are mathematically equivalent, and “acceleration up” gives us a Euclidean field wherever we want it, why should anyone prefer non-Euclidean math? Only a show-off would prefer fifty pages of calculations where he could get by with one page.

After all this, MM has come to the conclusion that the Gaussian field and the tensor calculus were imported by Einstein for reasons that are strictly ones of public relations. They are impressive in their own right, in the way of all esoterica, and it is fair to say that the math of General Relativity is as famous as the theory itself. Einstein's genius is that he chose just the right gown in which to dress his theory for the ball. An avant garde math was sitting around just waiting to be asked out by some ambitious theory, and Einstein had an eye for such matchmaking. Neither the field nor the math were really necessary to an updated theory of gravity, but Einstein worked very hard to make them seem so. He created an incredible amount of confusion, in part by infusing into his writing a mishmash of German philosophy and big, imprecisely used words (like epistemology), in part by writing in a very opaque style—a style that was and is a commonplace in science writing. This faux-haut style fooled most of his fellow scientists of the time. Where a truly learned discourse would have sent them running for cover, or simply confused them, a stilted sentence structure with a quasi-mystical lilt thrown in now and again was just enough to impress. In the case of General Relativity, it was sufficient to obscure the straightforward nature of the problem at hand and to seem to recommend the equally obscure math of Gauss in order to solve it. Not as much new confusion was necessary with General Relativity as with Special Relativity, since the reader was still reeling from all the murky sentences and murkier equations of the latter and therefore did not need many new clouds in his sky. Besides, most of the obscurity of GR would be provided by the tensor calculus.

Some feminists have recently tried to establish Einstein's first wife Mileva as an equal partner in his triumph if not his fame, and it may well be so. If it is, then she bears equal responsibility for the disaster of the tensor calculus, since it appears that she was the one who first recommended it. She was the professional mathematician. It may be that she was the one who saw the PR possibilities. (He gave his Nobel Prize for Physics in 1921 award to her after they divorced.) However that may be, it seems fair to say that it was Einstein himself who thought to rewrite Special Relativity with the tensor calculus in order to make it shine at Princeton. This seems proof beyond anything that the math was used as the primary selling point, since there is no other argument that can be made for using the tensors to solve SR. If the argument for making GR a Gaussian field is tenuous, the argument for making SR one is non-existent. Einstein has already stated that the SR field must be Euclidean and Galilean, by definition. It can therefore hardly benefit from the imprecision (free data) and unwieldiness of matrices and field equations.

Inertial System is Ignored in General Relativity

MM maintains that Relativity is true because we need time and length and mass transforms in the same way that Einstein said. And yet Relativity has not been interpreted correctly, by Einstein and others. The current transforms are in error, but close for the most part.

MM has maintained since the beginning that Relativity is defined by the need for transforms. If we require transforms, then Relativity is fundamentally true. Even if we require transforms only due to the Doppler effect, that still implies Relativity. The rest is a matter of interpretation and math. Einstein sometimes interpreted Relativity in the wrong way, and all his math is wrong, but fundamentally he was correct. We do require transforms, and we require transforms that are of the general form he gave to us. Our job is therefore to correct the math and the interpretation, in those places it fails.

Concerning General Relativity, the question becomes, “Do we need to apply these transforms to accelerations, to combine relativity with gravity?” Yes. Einstein was completely correct in this, so General Relativity must be fundamentally true. Einstein also manages to get the right numerical answer—or near the right answer—with his curved math and space, so we must give him some credit. But we must disagree with him in several ways. Previously in this paper MM showed that the curved math is not necessary. It adds a needless complexity. Even for those who do not or cannot accept expansion theory, GR can be done with a much simpler math.

That is to say, even if you want to keep gravity as a pulling force, it is much more efficient to reverse the accelerations in the math, and then apply the time differentials. This method is mathematically allowed, and it gets the right answer much more directly and with much less work. It also clarifies the mechanics. The simpler math puts the motions and forces in a higher focus than Einstein’s math was able to do, so that whatever your mechanics may be, you will have a firmer grasp of it with the simpler math.

This paper will clarify a second major disagreement that MM has with Einstein. He first wrote about this disagreement in his paper Born-Einstein letters on his site, but due to its importance it needs to be discussed further here. Not only does Einstein choose a curved math, he chooses a curved field. He lets his math define his field, so that the curvature of one is the curvature of the other. In Solving and Arguing General Relativity Problems without the Tensor Calculus (In about 1/100th the time) MM has already proved that this was simply a choice. By making a different choice one can also get the the correct answer. Einstein had implied that curved math was necessary, but that is false. The math can be done in either a curved field or a rectilinear field, with either curved math or Euclidean math.

In a curved field, certain mechanical properties are given to the field, and certain fundamental dynamical facts are the outcome. In letter 99 of the Born-Einstein letters, Einstein says, ''the gravitational equations would still be convincing because they avoid the inertial system (the phantom which affects everything but which is not itself affected).'' This quote cannot be circled and highlighted enough. In Einstein’s mathematical expression of GR, the inertial system is avoided, by Einstein’s own admission. What does that mean? It has been taken to mean that the equations have to do with acceleration, acceleration is “non-inertial”, and therefore the equations are non-inertial. This interpretation allows readers to pass over this quote of Einstein without pausing. But clearly Einstein could not have meant that in this quote. It would be silly to state something so obvious to another top physicist, much less to then call the inertial system a “phantom which affects everything but which is not itself affected.” In saying that he had “bypassed the inertial system,” Einstein was saying that he had bypassed the dynamical system of forces: he had bypassed the inertial system of Newton—based on force—which acted as a phantom by determining all motions. In Einstein’s math, the motions were determined by pre-existing curves, or by differentials from point to point in the field, not by phantasmagorical Newtonian forces at a distance. Einstein’s field is not an inertial or dynamical system, it is a mathematical system. A body in the system does not move in a curve because it feels a force, it moves in a curve because the space is curved, and the space is curved because the math is curved. It moves in a curve while feeling no forces!

Einstein saw this as a great advance, since it seemed to cleverly sidestep Newton’s problem of force at a distance. Newton had defined force, mass, and acceleration as functions of one another, but since the acceleration was a pull, the force appeared to be transmitted through empty space, with no physical mechanism. Einstein did not provide a physical mechanism: gravitons were of no interest to Einstein himself, as a mediating particle of this force. No, gravitons were proposed by Einstein only as carriers of gravity waves, and were proposed as fundamental field particles only after Einstein, by people who did not understand his concepts. Einstein did not want or need a mediating field particle, because his equations already avoided the inertial system. The equations were expressly chosen to avoid the inertial system, and without an inertial system, you don’t need to explain forces or accelerations. In fact, in Einstein’s equations, all forces and accelerations are only apparent. There is no centripetal acceleration, since the field is already curved. And even a body in freefall is not really accelerating. According to Einstein’s math, a body in freefall is experiencing a constant velocity, according to its own local measurements. It is simply moving into adjacent field “levels” where velocity is measured differently. Since these levels are not equivalent, mathematically, you need GR transforms to go from one to the other. The difference in velocities at different levels is therefore not a real acceleration, it is only a difference in transforms. According to Einstein’s postulates, the body does not accelerate, the transforms do.

Physicists after Einstein have continued to sell this interpretation as a thing of great mathematical and theoretical beauty, since it seems to solve Newton’s problem with one flick of the switch. The problem is, it solves the problem only by hiding it in the math. Einstein avoids the inertial system by making his math the cause of the motions. The curved math does all the physical work, with no need of real forces or accelerations. But clearly this is a cheat of gigantic proportions. It is beyond belief that he was never called on it. He was never called on it because no one understood how this curved math was really working, or how powerful it was as a heuristic tool. (See Why Non-Euclidean Geometry is a Cheat on MM's site.) The only ones who understood the math, those like Hilbert and Klein and Weyl and Minkowski, were thrilled to have it used in a famous physical theory. So they weren’t going to spill the beans. The mathematicians were the ones who had proposed the equations in the first place. And no one else could see through the veils.

To say it again, the problem is that you cannot let your math carry your forces. The math should represent motions, not cause them. In Einstein’s field equations, the motions are caused by the field curvature, and the field curvature is caused by the math. So it is the math that causes the motions. In curved math, the math becomes a force. The math becomes the first cause, the impetus to motion. The math replaces the inertial system. That is not a theoretical advance, that is a theoretical and mathematical cheat.

Look closely: Einstein has hidden the mechanism in his math, and, although the question is begged most assuredly, no one has seen where to beg it. Einstein has given us a curved field around a planet (say), so that we no longer have to ask how that planet acts on its moon. The field is curved and the moon follows the curve. But the question begged is this: “How does the planet act upon the field, to curve it?” With Einstein’s equations, the field curvature is given to us automatically. The math is curved before the first question or the first manipulation. So we forget to ask for a mechanical reason for the curvature, or a mechanical cause. At the very least we need a physical link between the planet and its field. “Why is the curvature greater nearer the planet and less farther away?” To this, Einstein has no possible answer. He has already matched his math to the known field, so any answer he could give would be circular. For Einstein, the answer is, “The gravitational field acts like it does because that is what a gravitational field is. We are given an experimental fact, and MM has matched his equations to it. That is what physics is. What further answer is possible?”

If Einstein had given this particular answer, he would have been following the dodge of Feynman. When pressed on theoretical contradictions, Feynman would always dodge into this “experimental” stronghold and bar all the windows. Physicists in the 20^th century loved this dodge, since it immediately pegged the opponent as some sort of metaphysician. It was if to say, “I am a hard scientist, and we hard scientists—opposed to, say, psychologists or sociologists—are tied to facts. We limit ourselves to questions that can be decided by experimental outcome. We don’t have time for metaphysical questions and squishy philosophical problems."

By couching logic as a squishy metaphysical question, physicists were allowed to propose theories in which there was no connection between the facts and the math, or as if mathematicians were allowed to propose equations in which there was no connection between the postulates and the deductions, between the axioms and the proofs.

For Einstein, his answer is a dodge because physics is and always has been more than matching a set of equations to an experiment. If the equations imply physical facts, the physicist should be able to make some physical connection between the equations and the facts. Otherwise you just have a math with no theory. Claiming that the math is the theory is like claiming that the roof is the floor.

To be more specific, there is an easy reply to the question “What further answer is possible?” That reply is: given a planet and a curved field around it, we want a causal mechanism for that curvature. If the planet is the cause of the curvature, as Einstein certainly implies that it is, then we must have a mechanism, or at least the theory of a mechanism. If we don’t, then the field is just as mysterious and un-physical as was Newton’s field of forces at a distance. In fact, curvature IS a force at a distance, since the field is at a distance from the Earth.

Notice that this last paragraph is not pointing out a metaphysical problem, but a mechanical one.

An even greater mechanical problem comes when we look at impulse to motion in the field. This is what MM is calling “the biggest black hole in GR”. If we have no real forces and accelerations in the field—all motions being caused by the field curvature at each point—then we have no impulse to motion on a non-moving object in the field. If we place an object at some altitude over the Earth, and use Newton’s field theory, we can explain its immediate fall by a force between that object and the Earth. Using the theory of expansion, we can explain its fall by the real motion of the Earth toward it. Using Einstein’s field theory, we cannot explain its fall. Yes, if it is already moving in any direction, we can explain its subsequent motion by field differentials. If it is already falling, we can explain its continued fall and continued apparent acceleration by field differentials. If it is in orbit, we can explain its continued orbit by the curvature of the math. Using Einstein’s field equations, we can explain any motion except falling from a state of rest. There is no mechanism in Einstein’s field to push the resting object from one level to the next lower one. Since there is no inertial or dynamical field, nothing is or can be impelling the body to move from one point to the other. Ironically, Einstein’s equations cover any possible motion in the field except motion from rest.

Amazingly, this point has never been raised, and it has never been raised because it is hidden in plain sight. It is so basic that no one has thought to look at it. Everyone knows that objects fall in a gravitational field, so how could a set of field equations fail to contain that? It doesn’t seem possible, so no one has checked it. But it turns out that it is the one experimental fact that disproves Einstein’s field equations. An object placed in a gravitational field will fall, therefore the curved math cannot be correct.

Once stated, this problem is so unanswerable it becomes humorous. If an apologist for Einstein attempted to refute me, he or she would have to say something like, “No, Einstein’s field equations do allow for motion in this case, since the equations not only create field differentials, as you put it, they create field potentials. As with the magnetic field, these potentials are perfectly capable of causing motion from a state of rest.”

If the apologist said this, he or she would be claiming that a field of no forces could move a body from a state of rest just by mathematical differences between one point and another. He or she would be claiming that a real mass could achieve a velocity from a state of rest with no force upon it, no inertial or dynamical system, no collision, no emission, and no mediating field particle. In other words, according to this “physicist”, a real body can be moved by nothing other than math.

Physicists will not admit that this solution is not physical; it will not bother them one way or the other. They have already been doing this for decade. They are not only impervious to logic, they are impervious to all experiment. The lack of experimental facts is not proof of the expansion theory, since no experimental fact is proof of a theory (see Karl Popper). Rather, it is proof against Einstein’s theory. Einstein’s theory, like Newton’s, cannot be correct, for strictly experimental reasons. We have to come up with something better.

That something must be something that is more mechanical, not less mechanical. Which is why string theory should be immediately dumped as a nuisance. Expansion theory may or may not be correct, but, joined to my new E/M field theory, it is already much superior to either Newton or Einstein. It avoids this black hole of GR, it avoids the black hole of the stable orbit (See Solution to the Ellipse problem), and it explains hundreds of things neither Newton nor Einstein could explain.

You will say, if that is so, why do I continue to confirm that GR is true? Didn’t I just accuse Einstein of a gigantic fraud, in using curved math to cause his motions? Didn’t I just show that the curved field was physically false?

Expansion theory does not overthrow GR, it includes it and re-interprets it, in a more consistent field math and more consistent logic. When MM does field equations with his own math and theory in Perihelion Precession of Mercury Explained and the Saturn Anomaly, MM has to do relativity transforms within the gravity accelerations, and in doing this he is doing General Relativity. Einstein’s GR is fatally flawed, but GR, as a broader physical theory, is only confirmed by my corrections to it. In the long run, what I have done is correct Relativity, not overthrow it.

Einstein derives the spacetime equations of Minkowski
from the light equations but Minkowski's Four-Vector Field is False

First written May 2003. Published this form October 15, 2004

In Appendix 1 of the book Relativity, Einstein derives the spacetime equations of Minkowski from the light equations, like this:
r = [x ² + y² + z²]^1/2
Where r is straight line distance, found by a three-dimensional Pythagorean theorem.
r = ct
(This is equivalent to x = ct in the light equations of Lorentz and Einstein. Light does not have to travel along orthogonal axes, obviously. It can travel in any direction the the 3-dimensional continuum.) so,
x² + y² + z² - c²t² = 0

Then, he assumes r' = ct'

But MM has shown that the two equations
r = ct and
r' = ct'
cannot both be true, because the assumptions of Relativity demand that the x and t variables be in inverse proportion. However, it turns out that the one that is wrong is the first equation, although that seems very odd initially. The reason is simple: the variables in that equation do not stand for how the unprimed system sees itself. In Relativity, the variables in that equation stand for how the unprimed system sees the primed system. The unprimed equation states the situation as seen from the "stationary observer." Therefore, these equations are measured from a distance.
r ≠ ct
r' = ct' and
r = ct'²/t

r = [x² + y² + z²]^1/2 = ct'²/t
r' = [x'² + y'² + z'²]^1/2 = ct'
x'² + y'² + z'² - c²t'² = γ ( x² + y² + z² - c²t'⁴/t²)
[x'² + y'² + z'² ] - 1 = γ{[x² + y² + z²] - t'²/t²}
            c²t'²                         c²t'²

That last equation is the corrected space-time transformation. r' does not equal r, so the transform γ must be used to complete the equality. This transform cannot be generated simply from the two light equations or from Minkowski's quadratic equation; more information is necessary. Einstein used the equation x' = x - vt to develop a transformation equation, but MM has shown that this method was faulty. So if you use γ = gamma = 1/√1 - v²/c² to complete the transformation, you will compromise the math once again: gamma is incorrect. The true value for the transform for one degree of relativity is
α = alpha = t/t' = 1/[1 - (v/c)].

The value for two degrees is
ω = omega = t/τ' =    1 - wv/c²
                              (1 - w/c)(1 - v/c)

MM derives these new transforms in An Algebraic Correction to Special Relativity and Refutation of Gamma

In his lecture of 1908, called Space and Time, Minkowski claimed that by setting his "four dimensional space equation" equal to one instead of zero, as follows,
instead of    x² + y² + z² - c²t² = 0
let    c²t² - x² - y² - z² = 1
he was able to thereby generate gamma without Einstein's lengthy theoretical proof or any of his equations. In fact, he said in that lecture that Einstein's Relativity Postulate "seemed to him very feeble" when compared to his own method. His method, he claimed, simply expressed an invariance within a predefined mathematical group, which he called G_c (the group of objects defined by the limiting speed of light). Minkowski claimed that an "easy calculation" allowed a mathematician to derive gamma simply from the above equation. [This is before he introduced √-1 to complete his math.] He did not supply this easy calculation in the lecture; however, the mathematician A. Sommerfeld completed the math in the publication of the lecture (English translation 1923, Methuen &Co.; reprinted 1952, Dover Edition).

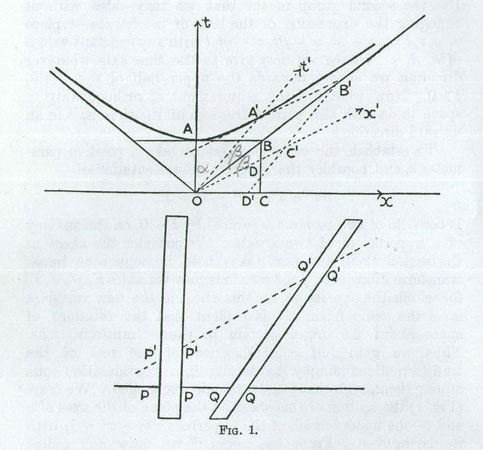
In the paper The Error of the M/M Interferometer, MM proves that both Lorentz and Einstein made the same basic error in conceptualizing the Michelson Morley Interferometer, and since MM knows that gamma is a phantom, MM reviewed Sommerfeld’s proof . In it Minkowski’s absurd hyperbolas have needlessly complicated the problem, and Sommerfeld is quickly lost.

Sommerfeld is obviously consulting the first part of figure 1 in the lecture more than the text, for near the beginning of his proof he assumes that OC’ (the “world line” of x’) is equal to OA’ (the “world line” of t’). But Minkowski states that “OC’ = 1 and OA’ = 1/c” (p.77, bottom, Dover). Sommerfeld also assumes, at the very beginning, that the angles of these lines to OBB’ are equal, which they cannot be if what Minkowski says is true [Sommerfeld assumes that the two angles that MM has pencilled in there as β are equal; but Minkowski himself contradicts this in the text]. With that, Sommerfeld’s proof has already collapsed.

Minkowski himself does a partial “easy calculation” on the second illustration of figure one, which consists of the “parallel bands.” These bands create triangles that are strictly equivalent to those of Michelson and Lorentz, although this is difficult to see at first. You can ignore the first illustration of the figure, the one with the hyperbolas—which is ironic. Just import the terms from the first illustration into the second one. Here MM simplifies Minkowski's math even further, to make it completely transparent.
PP = OC = x
QQ’ = OC’ = vt
QQ = OD’ = x’
x = ct
x’ = ct’
x = √x'² + (vt)²]
c = √x'² + v²t²]/t
c² = (x'² + v²t²)/t²
c² = x'²/t² + v²
c² - v² = x'²/t² = x'²c²/x² (c² - v²)/c² = x'²/x²
x/x' = 1/√(1 - v²/c²)

That is the easy calculation that Sommerfeld should have inserted, a calculation simpler than, but equivalent to, Lorentz and Einstein. It is simple, but mistaken. It is mistaken not in the way that Sommerfeld is mistaken. Sommerfeld is mistaken in that he does not follow the explicit instructions of Minkowski. The calculation above is mistaken because x ≠ ct and because both the v and the t in vt are undefined, as shown in An Algebraic Correction to Special Relativity and Refutation of Gamma. Minkowski imports the conceptualizations of Maxwell, Michelson, Lorentz and Einstein, but he does not recognize that their conceptualization are all faulty. He therefore makes no effort to correct them.

The question then becomes, is it possible to substitute MM's corrected calculations into Minkowski’s conceptualization? It is possible, and MM has shown how to do so above, simply by substituting the correct transform for gamma and by dumping x = ct. However, MM does not find that Minkowski’s setting of the four dimensional equation equal to 1 is at all helpful. Quite the reverse. Not only does it make the math more difficult, for no reason, it throws a blanket over the algebraic mistakes, making them much more difficult to unravel. [MM's simplification above is not difficult, but that is only because MM knew how to quickly gloss the mess Minkowski made of the problem.]

Like Einstein and Lorentz before him, Minkowski throws much more math at the job than it requires. He ends up offering a variant math that is just as dense and unnecessary as the math that came before. His solution is therefore not an improvement. Sommerfeld was not able to penetrate Minkowski’s arguments, nor has anyone else clarified this problem in the intervening century since the lecture. Minkowski is treated as one of the fathers of the new spatial math, and his conceptualizations stand to this day, faults and all.

Mathematicians like Minkowski’s four dimensional spacetime continuum for several reasons. The first reason is that Minkowski convinced fellow mathematicians that his equations more elegantly expressed the invariance of Relativity. And in a sense they do. It is not difficult to be more elegant than Einstein, whose exposition of the problem and its math was far from masterly. By a seemingly innocuous trick, Minkowski appears to create an invariant group that expresses c as a limiting aspect. But it does so at an enormous cost, a cost that no one has yet tabulated. Historically, Minkowski’s seemingly innocuous trick has both bolstered the incorrect math of Einstein and Lorentz, and hidden it from view. Because Minkowski failed to correct the mathematical errors of Relativity, his claim to confirm its transforms by a variant method has been disastrous. And because his method is mathematically even more subtle than that of Einstein, he made the problem that much more difficult to penetrate and argue. You have seen that some of the finest mathematicians of the 20th century were not able to understand Minkowski, including the man given the job of supplying extensive footnotes to the international publication of the lecture.

And this is even before Minkowski introduced s = t√-1 . The reason for doing so is again purely mathematical: the quadratic differential equation becomes symmetrical. But this is completely beside the point. The symmetry is a manufactured symmetry. Minkowski says, "Thus the essence of this postulate may be clothed mathematically in a very pregnant manner in the mystic formula 3 x 10⁵ km = √-1 seconds." As if we are in need of mysticism in physics! Besides, this equality is not mystical, it is false. Clothing a theory in false math is not pregnant in manner, it is impudent in manner. Making the quadratic equation symmetrical implies that time (or at any rate, s) travels orthogonally to x, y, z. But there is no reason to assume this. A mathematician will say that there is no reason not to assume this, if we want. It makes the math more stylish, if nothing else. But there is a very good reason not to do it. Importing more and more abstract math into a problem that is already in need of repair is very dangerous. The reason not use Minkowski’s math is simple: it hid the t variable in Relativity, making it impossible to correct the underlying algebra for a century.

Why Hyperbolic Math is inapplicable to General Relativity
The simple empirical proof that time does not travel
orthogonally to x, y , z.

In this paper MM shows direct empirical evidence that disproves a basic axiom of Riemann, Minkowski, and Einstein. It thereby falsifies the tensor calculus and the math of General Relativity. It does not falsify Relativity as a whole, and the intent of this paper is not to attack Relativity. My intent is to correct and fortify Relativity.

The evidence is absurdly simple and may be represented by a situation no more esoteric than a car going in a straight line. The only data MM needs to present is data showing that a car going in a straight line is capable of accelerating. There is no need to show a graph or to footnote any extensive experiments in support of this as it is obvious. Why does this data disprove the math of General Relativity?

For this reason: in a Cartesian graph representing the acceleration of this car, we would have x and t axes. We would plot x against t and find a curve. Now, MM was led to ask why the line on the graph curved and the line on the ground, made by the car, did not. You will say that it is simple. On the graph x and t are plotted against each other, but the axes are at a 90^o angle. This causes the curve. In the physical situation, x and t are not a 90^o angle.

That’s right, and MM's point is already proved.

For the car to be physically able to accelerate in a straight line, it must be true that t and x are varying in that same line. The time variable cannot have any possible angle to x. If the time variable had any angle to x, then the line would curve.

The car is describing a line on the ground. If this is not clear, put paint on the tires and drive for a moment. There will be a line on the ground. To mathematically explain that line there is only one way. The x variable and the t variable are in the same line.

You may say that the car is not truly going in a straight line, since the earth curves. But if you say this you are missing MM's point. When you start talking about the earth curving or the universe being a curved manifold or any of that, you are introducing y and z axes. MM is talking only about the x axis, and how t varies relative to it. My proof relies only upon the possibility of driving in a straight line on one axis or in one dimension. If it is possible, then x and t cannot be orthogonal.
     Someone versed in pettifoggery but not in logic will now say that it is impossible to drive in a straight line, since the universal manifold is curved in every dimension, according to post-Einsteinian physics. This person will argue that an apparently straight line will look curved from somewhere else, since straightness and curvature are relative to begin with. But this is also a misdirection in argument, since even though time and length are indeed relative, they still have only one value for each event in each frame of measurement. We must choose a frame of measurement, and once we do it is immaterial what someone in another frame thinks. I do not care whether my straight line looks curved to someone else, since I am not using his watch. I am using my watch, which is in my frame; therefore the only x that is important is my own. If I see the line as straight, then it is straight, no matter what you or god think of the matter. This is what relativity implies and must imply, not some mushy inability to measure.

In fact, there is no need to prove the line is straight at all since claiming that it looks nearly straight to me is more than enough to destroy hyperbolic math here. If my time moved at a right angle to my x then every accelerating real object I looked at must appear to my eyes to move in a hyperbolic manner. And not hyperbolic in some ultra-slow sense. No, hyperbolic in a quickly curving, immediately obvious sense, since we are assuming that the x and t of the car are changing at values very near to each other and to the number one. The hyperbola would be a slight curve only if x were very large and t very small, or the reverse. What we have in a straight line acceleration is two x axes and one t axis, all stacked (superimposed), and all in the precise same direction. Any angles, one to the other, would destroy the given situation.

Another problem is encountered when we look at the mathematical definitions of time and motion. Minkowski wants to allow time to move on the imaginary axis, which is orthogonal to the other three. But "motion" is a precise and unalterable thing, mathematically. A motion must either be a velocity or an acceleration, constant or variable. This motion is expressed with distance in the numerator and time in the denominator. But we arrive at a problem if our denominator is orthogonal to our numerator, since we can't express a velocity or acceleration that way. Orthogonal vectors cannot be put into ratios, or fractions. This is a basic rule, and perhaps Minkowski was at too great an altitude to remember it. But it is as true now as it was in the time of Archimedes.

The tensor calculus relies on hyperbolic math, which uses i, the square root of –1. In order to create the field of hyperbolic math, one must assume that the t variable travels orthogonally to x, y, z. That is to say, at a right angle. MM has just shown that the t variable does not and cannot travel or vary or change at any angle to x, y, z. Therefore the hyperbolic math is physically false.

You might say that this is one exception, but that in general the tensor calculus still may be used, but all cases are exceptions. This is just the most obvious exception. In no physical case does t travel orthogonally to x, y, or z. All you have to do is actually study the mechanics of any real problem and the mathematical operations that are done to solve these problems. If you do this it quickly becomes clear that t is always internal to x, y, z. It must be since in any particular problem, t is always a second measurement of either x, y, or z.

The math of Riemann and Minkowski was adopted by General Relativity because it seemed to be a poignant way of expressing the problem. Four-dimensional space, where the time variable is treated just like the other three, has turned out to be very seductive to the general imagination. Its mystifications were just the right flavor for the 20th century. But it is time to get back to work. Hyperbolic math is not applicable to physics, since it grossly misrepresents the time variable. If we want to continue to use it for reasons of efficiency, we must do so with full recognition of its conceptual limitations and contradictions. It would appear that this conceptual falsehood just proved is fatal. It has already caused terrible theoretical problems and it will continue to do so as long as it is used in such a cavalier manner.

None of this implies that the other axioms of Special or General Relativity are false, only that the axiom of hyperbolic math is false. Relativity is true, including time dilation, length contraction, and mass increase. There can be no doubt of this, but that MM recommends the discontinuation in General Relativity of hyperbolic math and of the hiding of the t variable in the concept of i.

Relativity shows the mathematical relation of time to the distance variables, and in this it is not wrong. There is a certain mathematical equivalence between time and distance, as is shown in the equation x = ct. Einstein and Lorentz saw this equation as representing the speed of light in a given coordinate system. (More Problems with the Friedmann Metric on MM's site.) Although that assignment of the equation is wrong- since it contradicts postulate 2 of SR—it can be used as a direct transform between time and distance, where c is the very simple transform. But in no case does time travel orthogonally or externally to x, y, z. This should have been known from the start, since the other postulates of Relativity imply it very strongly. If x and t are so easily transformable, in such a simple equation as x = ct, then the two variables cannot be traveling at complex angles to one another. We simply cannot use hyperbolic math with confidence in physical situations.

You will say that hyperbolic math is perfectly applicable, since it allows us to get the right answer. That is to say, it yields the correct number. Even if that were true, it is not (see The Easy Solution to the Saturn Anomaly.) Applied mathematics must be more than getting the correct number. If applied mathematics does not also give us the proper concepts, then it has failed. The 20th century has been very short on mechanical explanations, and the mathematics has taken the place of the mechanics. That is to say, the mathematical concepts have become conflated with the physical concepts. That is precisely why string theory is postulating curled up dimensions and other esoterica. (See Critique of String Theory: the inelegant universe) Theoreticians have long since begun to let the math lead them into physical assumptions and physical theories.

Minkowski allowed the time variable to be orthogonal to the other variables simply to keep his math symmetric. He did not care a fig for any physical implications, and said so. But his cavalier attitude has allowed many modern physicists to assume that a rather meaningless mathematical postulate is the same as a physical reality. Many if not most contemporary physicists believe that time really does "travel at a right angle" to x, in a mechanical or kinematic sense. This belief has spawned many other theoretical absurdities and contradictions, and has led directly to a muddling of their understanding of many concepts, including "dimension", "event", and so on. Applied mathematics must return to a scrupulous accounting of concepts, in order to prevent any more mathematical concepts from crossing over into physical theory unnoticed and ultimately unanalyzed. (Link to Why Non-Euclidean Geometry is a Cheat on MM's site for a fuller critique. )

For much more on this problem, see multi-part analysis of the Einstein field equations on MM's site which revisit this problem in finer detail, including a line-by-line critique of Einstein's 1916 paper.

The Light-speed Submarine Problem

In July of 2003, Physical Review D published a report on the “light-speed submarine problem.” This is a problem several decades old that many top physicists have spent much time on. A couple of them are said to have found solutions, including an SR solution in 1989 by James Supplee and a GR solution by George Matsas in 2002. A reader sent MM a link to this report because Supplee solves by letting the ocean (but not the sub) accelerate upwards at g. The reader thought MM would be interested in this, since it mirrors his SR solutions of GR problems. (See Solving General Relativity Problems without the Tensor Calculus (In about 1/100th the time.)

This problem and its solution is an example of the Einstein's failure to consider the reference of the local coordinates, namely those of the submarine in this problem. The answer is that the problem is misdefined from the beginning: We are given a submarine moving at a speed near c. Since observers will see the submarine as shorter and denser, they would expect it to sink. Why doesn't it?

It does not sink because what the observers see entails nothing about the local mechanics of buoyancy. Relativity is a math that supplies transforms for data. The data is skewed by the relative motion. It is this skewing that causes the need for the transforms. The local data does not match the observed data, so transforms are required. But of course this means that, logically, the observers are not observing the local relationship between the sub and the water. If they were, they wouldn't need transforms. It is the local relationship between the sub and the water that determines whether the sub sinks or floats, so what an observer sees is mechanically immaterial.

The local relationship between the sub and the water is not affected by Relativity, since Relativity requires a distance separation. Locally, the sub is neither shorter nor denser than it was at a slower speed, so the whole problem is a manufactured one.

We are given another problem, that being that the sailors inside the sub would see the water getting denser, which would make the sub move up. But even supposing that submarines had windows, this is again a manufactured problem. Both SR and GR require a time separation, so only water at some distance would be measured as denser. But the sub is not moving through that water. The sub is moving through local water. Since Relativity does not apply locally, what the sailors see or measure in this case is again mechanically immaterial.

These physicists are only wasting time “solving” a self-created contradiction, and they are doing this because they don't understand the first postulates of Relativity. They assume that what distant observers see is physically determinant, when it cannot be. What observers see is different from local numbers. If it weren't, there would be no need for Relativity. But two sets of numbers can't both be physically determinant. As a matter of buoyancy, the submarine can only have one length and one density. The local numbers are the ones that determine the physics. The observed numbers are only observed. That is, they are false.

Notice that MM is not contradicting Relativity, only in it's application. To state it plainly, to have Relativity you have to have two co-ordinate systems and therefore two sets of numbers. Both sets of numbers are valid, in the sense that the data is significant for both. But both sets of numbers cannot determine the mechanics, since the submarine can only do one thing at a time. It cannot both sink and float. Clearly, the local numbers must determine the mechanics, and the local numbers simply consist of at-rest numbers. If you are given only the observed numbers and want the local numbers, you just have to work the transforms backwards. In a nutshell, that is probably what Supplee and Matsas are doing. But if you want to answer the question as stated, you don't even need to go to that trouble. The answer is that the observations don't cause the sub to sink or rise, because observations don't cause motions. Local relationships cause motions.