Solving and Arguing General Relativity Problems without the Tensor Calculus (In about 1/100th the time)

Easy Solving (or go to Easy Arguing)

Miles Mathis has taught his students some wonderful mathematical shortcuts over the years, but this one is probably the most useful and the least known. In fact, it may not be known at all, and so this paper. It is a mathematical manipulation only and has no necessary physical meaning, but it confirms the postulates of Einstein in a beautiful manner nonetheless.

The postulate that is supplied by MM with this shortcut is the famous equivalence postulate, which states that gravity and acceleration are mathematically equivalent. In his lovely elevator car in space, Einstein showed that there is no difference between acceleration up and gravity down. After reading this, MM decided to take Professor Einstein literally, and he reversed the vector by hand in several famous problems. This vector reversal had the mathematical effect of turning the field equations inside out. The objects in the field got larger with time, but the space around them reverted to a rectilinear or Euclidean field. In this field MM could do very simple math, achieving the same numbers as Einstein. Then, when he was finished, MM just turned the vector back around, to suit myself.

An example of the simplicity of the process is in solving the precession of the perihelion of Mercury. (A more detailed study on this problem is in "The Perihelion Precession of Mercury" Einstein told us this was caused by extra curvature from the Sun, so MM will solve by looking at light move from the Sun to Mercury. Like Einstein, he assumes that any influences from the Sun will move at the speed of light and that the curvature will reveal itself through the gravitational field. To get this revelation, MM just let the Sun and Mercury accelerate at their own known rates, and watch the curvature.

Since the light moves from Sun to Mercury, the Sun’s acceleration happens after the emission, and is not part of the math. We only need to look at Mercury’s acceleration. Once we turn the vector around, Mercury will move in all directions, but we need to look at only one of them. We look in the direction of the orbital motion, which is tangent to the Sun. This one motion will show us the curvature, as you can see in the diagram.

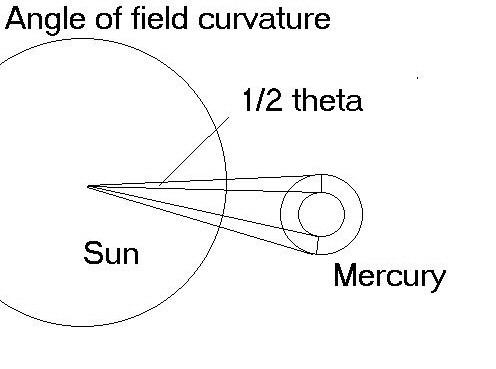
At perihelion, Mercury’s orbital distance is about 46 million km. Light travels that distance in 153.3s. The acceleration at the surface of Mercury is 3.7m/s², so we find that one surface of Mercury will travel this far while the light is in transit:

s = (3.7m/s²)(153.3s)²/2 = 43.5km

That gives us the field curvature in one direction, but we want the total field curvature. The orbit has extension both +x and –x in the field over each dt, so we must double our number. Then we just find the angle of curvature created by the total acceleration in that time.

tanθ=87,000m/4.6x10¹⁰m
θ = .39 seconds of arc

If we use the mean orbital distance instead of distance at perihelion, we get .49 arcsec. Einstein’s field equations use both distances, since precession occurs at perihelion, but the curvature occurs over the entire orbit over a year. This is why his number, .45, just about splits the difference.

If you think that was a coincidence, watch the same solution applied to the bending of starlight by the Sun covered in more detail in The Aberration of Starlight is an Expanding Earth. We let the light pass the Sun and then travel to the Earth, where we see the bending. To calculate the amount of bending, we note the time it takes for the light to get here from the tangent, which is 501s. Once again, we reverse the acceleration vectors, but once again the Sun’s acceleration happens after the light has passed. So we just look at the Earth’s acceleration in 501s.

s = (9.78m/s²)(501s)²/2 = 1,230,000m
tanθ=1,230,000m/1.51x10¹¹m
θ = 1.68 seconds of arc

This is very near the number Einstein got (1.7), and this time we get the right amount without any doubling, since we don’t need the entire field curvature here. Bending and precession aren’t the same phenomenon. Mercury’s light is getting bent in both orbital directions, since the planet as a whole is experiencing precession. But only the observer on the Earth is seeing the bending, so once we reverse the vector, it is his experience that is bent, not the light. As you can see from the diagram, the light is not curving. Only his measurement of it is. Since the observer is only on one position on the Earth, the bending uses only half the field. In order to see the curvature of the whole field, the observer would have to be on opposite sides of the Earth at the same time—an obvious impossibility. (To see why this number does not match the current number 1.75 go to The Aberration of Starlight is an Expanding Earth where it is gamma that causes the current equations to fail. The number 1.75 is an outcome of the current equations, not of the newest measurements.)

All other General Relativity problems that can be solved or estimated with this method are many like How General Relativity Solves the Metonic Cycle of the Moon

How to Win an Argument about Relativity most Efficiently

This paper will show you how to win an argument about Relativity very fast, even if you are arguing with professional mathematicians who start misdirecting with tensors. You don't have to know the first thing about tensors to win an argument about Relativity.

My polemic here is not for those who believe Relativity is a hoax. It is not for anti-Relativists. It is only for people who think Relativity is misinterpreted, incomplete, or mathematically flawed. MM has shown that although the transforms are presently incorrect, they can be fixed.

The fact is, Relativity is flawed mathematically in many places. And it has been badly misinterpreted. That said, the basic concept is correct. The finite speed of light does require us to develop transforms to apply to data coming in from long distances, and the historical proofs of Relativity—by Einstein and others—come close to supplying us with the right ones. Despite many fudges in the math, the mathematicians have managed to push the equations back to the data in many cases.

My argument here is for you to use only when you are countering some mainstream stuffed shirt who tells you that Relativity is bedrock, confirmed to within an amoeba's eyelash. It isn't. Like all other current math and physics, it is mishmash of pushes and finesses. It has needed a lot of cleaning up for over hundred years, and it has never gotten that clean-up in the mainstream. As it stands now, it is very very dirty.

A good debater will lead with his best card first, to put his opposition off balance from the beginning. Our best card is the lack of a velocity transform. Whenever someone unloads a pile of tensors on your head, just tell him or her you would like to see the transform for velocity, in either tensor form or any other form. The secret: there isn't one. The current transforms include a transform for time, length, momentum, mass, and energy, but no velocity transform. Watch out, because your opponent may try to pass the addition of velocities equation by you, to fill the void, but don't let him.

V = (w + v) / (1 + wv/c²)

Say, “No, that is the addition of velocities equation. I want the velocity transform.” The addition of velocities equation has three velocity variables in it, and it is to be used when you have a velocity inside a velocity. What you are asking for is a velocity transform to go with your time and length transforms. In those transforms, you get a transform from x to x', say, or from t to t'. Ask for a transform from v to v'.

Odds are, your opponent will immediately begin to shrivel up, because Relativity in its current form has no velocity transform. The math doesn't exist. There is no v' in the equations, and no way to calculate it. At the level of t' and x', there is only v. Einstein takes the velocity between S and S' to be v, and so there is no v'. Your opponent may try to tell you that Relativity is symmetrical around velocity, but don't let him get away with it. It isn't. He may say something like, “Relativity is covariant (or invariant), so velocity is symmetrical.” But that is a mishmash. It is true that Relativity is covariant, but that doesn't imply that velocity is symmetrical. What covariant means in Relativity is that the laws of physics are the same no matter what point of observation you choose to calculate from. Which means that it doesn't matter if I measure you or you measure me. The laws and transforms will be the same form. That much is true. If I am going v relative to you, you are going v relative to me. But in the actual equations of Relativity, S and S' aren't symmetrical, because although S is “me measuring you,” S' is not “you measuring me.” In the current transforms, S is “me measuring you,” and S' is “you measuring you.” There is no symmetry between those operations, you see.

This all goes to say that there should be a velocity transform, but there isn't. Velocity is x over t, and we have an x transform and a t transform. Why would we not have a v transform? You would think they could just put x' over t' or something, and get one that way, but it isn't done. Why? Because it would get the wrong answer, and it would screw up the rest of their equations. So they just skip it. They hide it. They pretend the problem doesn't exist, and they cover it over as fast as they can with a big pile of tensors.

Your opponent might say, “Can you give me an example of where you would need a velocity transform?” Thinking you won't be able to. But just say this: “OK, what if your satellite has an onboard clock. It travels from Mars to Jupiter. The distance is known, so the satellite measures its own time to travel, then calculates its own velocity, sending this data back to you. Your satellite has a powerful reflector, and you have a powerful telescope, so you can actually see your satellite as it travels from Mars to Jupiter. You time the travel with your own clock, use the known distance, and calculate a velocity. Unfortunately the velocities don't match. You need a transform.”

Your opponent will say, just use the time transform. We are given the same distance either way, from previous data, so it is the time that causes the discrepancy. Yes, that's right, but your opponent has just admitted the existence of a v'. It is the velocity as measured from the satellite. Which means there was no symmetry regarding velocity. Which means the laws of Relativity are covariant, but the transforms are not . Which means the variable v in the original SR proof is undefined, which means the proof is flawed. The first equation of the proof, x' = x – vt, is false, which dooms the entire proof.

Another problem is that, since the current time transform is wrong, your opponent will get the wrong answer anyway. The time transform has been tweaked to make the energy equation in Relativity work out (see below), and if you use it in the current form to calculate a velocity, you will get the wrong answer. In other words, the time transform that is necessary for this velocity transform isn't the time transform that is necessary for the energy equation. If you start calculating velocities this way, it just shows up this inconsistency, so that is why they never calculate velocities.

This problem with symmetry and v' has caused many failures in Relativity, but the biggest one is that the central term in the tensor calculus is false. Basically, the current motor of General Relativity is the tensor calculus, and the central engine of the tensor calculus is a term called gamma , which still is expressed like this:

γ = gamma = 1 /√(1 - v² /c²)

In short, the tensor calculus is a method for going from any S to any S' using angle cosines. Rather than write out the angle cosines, the tensor calculus expresses them as some letter with subscripts or superscripts, like l_ij. These variables are then collected in a matrix, and the tensor calculus keeps track of them.

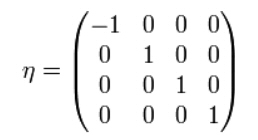
That's one of the simplest matrices, called the Minkowski metric. It represents flat spacetime or a normal Euclidean field. MM does not to give a full lesson in tensor calculus, but he will show you enough so that you understand how it is a misdirection. Already you can see that it is not a simplification of the math. Rather, it is an unnecessary complication, used to hide problems in the simple math. That “4-vector” can just be written t, x, y, z. The metric doesn't tell you anything you didn't already know.

Although it is clear that the Minkowski metric is a ridiculous complication of simple algebra regarding the Euclidean field, we are told that the tensor calculus is a great tool when we begin looking at gravity fields, because in that case we have a lot of variables to juggle in a curved field. At first glance, that appears to be true, but it turns out to be false as well. Why? Well, notice that the tensor calculus takes us from any S to any S'. It is a method of transference of variables from one coordinate system to another. The masters of this math tells us we need a tool to do this, since General Relativity is a math of transforms from system to system. But it turns out that all of that is false since in the previous section we can do General Relativity in one Euclidean system. There is no need for multiple coordinate systems, therefore there is no need for the tensor calculus. The tensor calculus does not make the calculations shorter or easier, it makes the calculations much longer and much more difficult.

If you tell your opponent this, he will say something like, “You clearly don't understand Relativity. Doing field math in one Euclidean system is Newtonian, by definition. There is no way to do General Relativity in one flat system.” But there is. From the beginning, General Relativity was not defined as a curved field. General Relativity was defined as the application of time and length and mass gravity field of Newton, and that is what General Relativity is. General Relativity is Special Relativity plus gravity. Einstein then chose to do that with non-Euclidean math, but that was a choice, not a necessity. He may have thought it was a necessity, because he was convinced that the gravity field was curved and could not be uncurved. But MM has shown that the gravity field can be uncurved by one mathematical manipulation: simply reverse all the gravity vectors in the given problem.

In fact, Einstein showed the legality of that manipulation himself, in his own books. As the lead-up to General Relativity, Einstein tells us about the equivalence principle [see p. 66, Relativity, Albert Einstein.]. He does a thought problem to prove the equivalence principle, using his elevator car in space, and his proof is still is accepted to this day. Well, the equivalence principle the reversal of the gravity vector. Einstein proves that the math stays the same before and after the reversal, so MM just reverses the vector. Reversing all the vectors in a given problem uncurves the field. You can then do your time differentials and other transforms in that Euclidean field, with simple high school algebra. MM has rerun the central famous problems of General Relativity this way, getting the same answers as the tensor calculus in a fraction of the time.

This undercuts the entire raison d'etre of the tensor calculus. MM has proved that it is not only unnecessary, it is far slower. He did not had to attack the tensor calculus as a math, since he agrees that it is legitimate math and in some problems is useful. But in General Relativity it is not useful. It is an unnecessary complication and nothing more. More than that, it has historically been an obstruction, since it has covered up problems in the simple math. Because it renames and hides the original variables, it has prevented them from being analyzed and corrected. That is the second big card in your hand: the tensor calculus is misdirection.

Now, back to gamma . The early problems in the proof of Special Relativity that prevented Einstein from finding a v' caused him to find a form and value for gamma that was incorrect. The current time transform is t = γt₀. That is what they currently use in the tensor calculus. Unfortunately, that isn't what Einstein found. If you check his 1905 paper displayed in a separate screen, you will see that he found:

τ = γ(t - vx/c² )

If we put that into current notation, it is

t' = γ(t – vx/²)

Somehow they just managed to dump the term vx/c². But it is clear at a glance that the term can't ever be zero, unless x or v is zero. If x or v is zero, then we aren't in a relative situation. Relativity requires a velocity and a separation. But it is even worse than that, since gamma isn't correct, either. MM has found that the real time transform is:

t' = t/(1 – v/c)

Or, for two degrees of Relativity

t''/t = (c² - wv) / (c - w)(c – v) = (1 – wv/c²)/(1 - w/c)(1 - v/c)

Since the time separation term is messed up from the beginning, all the other uses of gamma are also wrong. The tensor calculus currently assumes (without proof or with badly finessed proofs) that L = L₀/γ
m = m₀γ (mass)
V = V₀/γ (volume)
T = T₀/γ (temperature)
Q = Q₀/γ (heat)
S = S₀γ (entropy density)

Since gamma is false, all those equations are false. That is the third big card in your hand: gamma is false.

As a fourth big card in your hand, you can now play this one. If we go back to Einstein's original papers and books and study his proofs, we find that gamma and all the transforms are derived from Lorentz's light equations. These were just simple equations of how light traveled in S and S'. They are x = ct
x' = ct'

Those equations are still accepted. No one has overturned them or questioned them in over a century. Unfortunately, they contradict the transforms currently used in the tensor calculus. Specifically, these two:

L = L₀/γ
t = γt₀

As you can see, length and time are inversely proportional there, since gamma is in the numerator in one and the denominator in another. That is physically correct: time and length must be in inverse proportion in the field equations. Why? Because we normally put one in the numerator and one in the denominator. As in the velocity equations, v = x/t. They also have to be in inverse proportion because Relativity wants length contraction and time dilation. Length gets smaller as the time period gets larger. That is an inverse proportion. Problem is, that doesn't match the light equations of Lorentz. If we set c equal to c, we get:

c = x/t = x'/t' x/x' = t/t'

Those are in direct proportion, not inverse proportion. As x gets bigger, t has to get bigger as well, or c will change. Inverse proportion would be

xt = x't'

You may ask your opponent how Einstein managed to prove that time and length are inversely proportional by assuming they were directly proportional. The proof must have been fudged somewhere, right? In fact, in Einstein's 1905 paper, he found them still directly proportional, even after finding gamma:

t' = γ(t – vx/c² ) x' = γ(x – vt)

Did Einstein correct that later or something? No. In 1920 he was still using the same equations [see p.33, Relativity, Albert Einstein.]. Notice that neither x nor t is written as over gamma. No ratio in either equation, which means they are still directly proportional. So how did they end up with L = L₀/γ in the tensor calculus? They must have done a switcheroo as they were re-building the tensor calculus, while Einstein wasn't looking. Either that or they need to convince you that x and L aren't the same. One is length and one is distance, they will tell you. All you need to say is, “Oh, so you are telling me that as distance gets larger, length gets smaller?” And watch the verbal gymnastics as they try to convince themselves of that. The only way they can achieve this switcheroo is to redefine Einstein's own explicit variable assignments. Einstein said in clear language that x' was an x-separation from the origin in S'. [ See diagrams on p. 32 of Relativity, Albert Einstein.] If we place an object in S', then the length of that object must change as the value of x changes. You cannot have the object appearing larger as the coordinate system shrinks, unless the object is unattached to the system. They would have to tell you that the position of the object was in S', but its length wasn't in S', which would be a curious argument.

Actually, they are right to make the switch, since Einstein was wrong. As MM has said, time and length have to be in inverse proportion. But the problem is, they just make a few switches like this at the end of the proof to suit themselves, leaving the proof itself untouched. You can't just push a proof to match data, claiming the proof still stands. If you have to flip variable assignments like this, it means you should have to rerun the proof from the beginning. No one has bothered to do that,probably because they can't figure out how to do it. If they did it, they would find that the problem with Lorentz's light equations causes both the loss of v' and the failure of gamma .

They will then tell you that Relativity has been confirmed in the lab. But you may tell them that is because only some of Einstein's equations are actually used. The rest are buried. Most of the transforms aren't actually used, except in textbooks. In real-life situations, most problems are solved down from the energy equation, and the energy equation just happens to be nearly right (more right than the other transforms, anyway). The current energy transform is:

E = γmc² = mc²/√[1 – (v²/c²)] After pages of corrections, MM found

E_T = m_ric² ([1 + (v’/2c)]) / [1 – (v’²/c²)])
which is only a small correction in most situations. For instance, at .1c, their transform is 1.005, mine is 1.06. This solves things like the Pioneer Anomaly without overturning the whole Relativity cart.

That is why Relativity currently works, sometimes. It is luck, not a good proof. The calculations have been pushed back toward the data for decades, and that is the only reason Relativity remains fairly successful.

When you tell them that, they will answer, “No, there is no room for a correction like that. From five thousandths to six hundredths is not a small correction. The current equations are already better than that.” But that is an outright lie. The current equations aren't better than that. In most situations, current physicists can't even figure out how to run the field equations, as MM has shown. Either they run them when they don't need them, as in the muon problem (See The Mysterious Muon), where they claim time dilation simply because they can't do the vector math. Or they run them upside down, as in the Pound-Rebka experiment on MM's site. Or they run them in partial form, as with the Mercury perihelion problem (See Perihelion Precession of Mercury Explained and the Saturn Anomaly), finding what they wish to find and ignoring whatever doesn't fit.

These physicists apparently do not have clue how to do the real math, so they run some horrible finesse for a couple of pages, pushing the equations to the data. MM has not studied the data and equations from the Pioneer Anomaly, since they haven't released it to the public. However having studied the mainstream's use of the field equations and transforms in many real problems and having never once found a series of equations that wasn't fudged in the worst possible way, MM suggests that this anomaly will be easily explainable by correct math also as with Einstein' gamma mistake.