Miles Mathis: E ≠ mc2 (Gamma is Kappa)
A
Complete Re-Derivation of E=MC2
How Corrected Transforms in Special Relativity
affect Mass,
Momentum and Energy Equations
| Please note that this paper is a simplification by me of a paper or papers written and copyrighted by Miles Mathis on his site. I have replaced "I" and "my" with "MM" to show that he is talking. All links within the papers, not yet simplified, are linked directly to the Miles Mathis site and will appear in another tab. (It will be clear which of these are Miles Mathis originals because they will be still contain "I" and "my".) The original papers on his site are the ultimate and correct source. All contributions to his papers and ordering of his books should be made on his site. (This paper incorporates Miles Mathis' emc paper combined with some sections of the emc2 paper and five paper. |

Einstein
First written October 2004
Introduction
In
this paper Miles Mathis derives new transformation equations for Mass,
Momentum and
Energy. He shows that Einstein, despite using a
thought problem that was useful and mostly correct in variable
assignments, made several crucial errors that compromised his
final equations. The thought problem of concern here is in his short paper of September 7, 1905, http://einsteinpapers.press.princeton.edu/vol2-trans/186 Does
the Inertia of a Body Depend upon its Energy Content? (The 1923 English
translation modified the notation used in Einstein’s 1905 paper to conform
to that in use by the 1920’s; for example, c denotes the speed of light, as
opposed the V used by Einstein in 1905. In this paper Einstein uses L to
denote energy; the italicised sentence in the conclusion:
If a body gives off the energy L in the form of radiation, its mass diminishes by L/c2
may be written as
the equation “m = L/c2
” which, using the more modern E instead of L to
denote energy, may be trivially rewritten as “E = mc2”.)
Fully half of this Miles Mathis paper is devoted to analyzing, critiquing and expanding this thought problem and its math. (Sections of an emc2 gloss of this paper are inserted in places.) The rest of the paper is devoted to a variant thought problem MM devised to clarify Einstein's variable assignments and conceptual assumptions. This thought problem yields new equations that answer many of the embedded mysteries of relativity and mass transformation.
Einstein's paper has long been a source of confusion. It's brevity and opacity have made its underlying concepts quite difficult to unravel. As with the time and length transforms of Special Relativity, the mass transforms that this paper yielded have never been corrected. They have been confirmed to the satisfaction of most experimental scientists and therefore the math to derive them has become a moot point. It was long ago swallowed up by much more complex math, including hyperbolic fields, imaginary numbers, Hilbert spaces, Hamiltonians, Lagrangians, and the tensor calculus. Although thousands of papers have been written on the mass transforms, no one has so far offered a crystal clear explanation of Einstein's algebraic variables and equations. In the past half-century, no famous physicists or mathematicians have even attempted to do so. Some have glossed the derivation as presented by Einstein, but none who accepted his final equations have provided a superior groundwork for them.
Now, a century later, only those who do not accept the final equations spend time on the mass transforms. And they do not attempt to clarify Einstein's mistakes. Rather, they present a variant math that makes more sense to them. Some of these variant maths have a certain validity, but MM believes that none will be looked at seriously until Einstein's math is proven to be false. That is what MM's paper does. A falsification of Einstein's algebra will be a falsification of all the higher maths that rest upon it.
(From MM emc2 gloss)
By making a couple of small corrections in Einstein's derivation, it was possible to derive the classical energy equation from Einstein's own equations, showing that
K = κmrc2 – mrc2 = mv2/2
In short, a new transformation term kappa was derived to replace gamma. This term was derived directly by making simple algebraic corrections to Einstein's paper of 1905. This new term elegantly shows the equivalence of Einstein's math and Newton's, as regards kinetic energy.
In deriving the classical energy equation from Einstein's postulates and math does not falsify the major findings of relativity or suggest that science should return to Newton. Relativity is true. Distance, time, velocity, mass, momentum and energy all require transforms from one observer to another. Beyond this, Einstein was correct in his other postulates, such as the fundamental postulate of energy transformation—that energy and mass are equivalent and transferable. The corrections will actually have a greater impact on the math and theory of General Relativity. The basic theory of Special Relativity—that is, relativity caused by velocity—has not been greatly altered by the corrections; only the math is changed, and, for the most part, subtly.
Nor is the resuscitation of mv2/2 to be understood as a return to Newton. Newton's equation is not a transform and does not allow us to go from measurement by a object to measurement by an observer. The variables in Newton's equations are all as measured by the observer. They are therefore not relativistic and are useless as transforms. MM only means to show the true mathematical link from classical kinetic energy to relativistic. A simple correction to Einstein's math shows why Newton's equation worked and continues to work in the proper situations.
And, perhaps most importantly, this new derivation shows that c is not a limit where mass goes to infinity. Since Einstein's equation is not an infinite series expansion of Newton's, c is no longer a limit in the math. In other words, Miles Mathis' proof below shows that gamma is incorrect, which means that there is no power series or infinite terms, which means that c is not a mass limit. Einstein's equation and Newton's equation are mathematically equivalent, and one does not "approximate" the other. This solves the so-called mass gap in Yang-Mills, among many other things.
(End of MM emc2 gloss)Einstein's paper is a compound—and sometimes a compensation—of several basic algebraic errors. Although in the body of the paper MM will prove these errors exhaustively, here MM will just gloss them. Firstly, he incorrectly applies his time transform gamma to the planes of light. Secondly, he misapplies the term m0c2 at the end of the derivation, giving it to the body rather than to the planes of light. This is difficult to understand, since the final equation contains the variable L, which he has explicitly given to the light. Despite these two errors Einstein arrives at a transform that is very nearly correct. That transform is again gamma
Einstein then solves down from this energy transform to find a mass transform, which is likewise gamma. But in this case he is wholly mistaken: his misassignment of variables has cost him needed clarity, and gamma is not even an approximation of the correct mass transform. This mistake has rarely been seen, since in experimental situations mass is always calculated from energy equations. In working with subatomic particles, for instance, the naked mass transform equation is never used. Values are arrived at from energy equations. As MM said, Einstein's energy equation is almost correct.
| The term for gamma
is γ= 1 √[1 - (v2/c2)] Miles Mathis proves, by
correcting the math, that the energy transform for Einstein's problem
|
You can see that the difference is very small in most situations, and might pass for decades without final experimental confirmation, especially in a milieu that considered Relativity a settled question. Physical Review Letters, the primary publication of record in the US, doesn't even have a category for Special Relativity. A scientist could not present a finding if he had one.
In comparing kappa and gamma, it is also important to note that MM proves below that Einstein's thought problem is not directly analogous to the more common experimental problem of a sub-atomic particle in an accelerator. MM shows that the energy equations must vary from problem to problem, depending upon the physical situation.
| In
deriving this new transform Miles Mathis also discovered several other facts
of great interest. One of these is that E ≠ mc2. If we assume that the rest energy is given by the rest mass—as in Er = mrc2—then the moving energy cannot be given by the moving mass, in a straight equation. A transform is required here as well, and it is not gamma. This is a consequence of Einstein's own variable assignments. Einstein assumed, with no theoretical or mathematical backup, that mc2 must be the term that is applied to the final energy E. It turns out that this is not the case. MM's new derivation, where all the variables are rigorously assigned, will prove that the classical equation is precisely equivalent to the relativistic equation. In other words, K = κmrc2 - mrc2 = mv2/2 |
Simply by correcting the math of Einstein's own thought problem,
MM arrives at a new energy transform κ that is nearly
equivalent to γ. This new transform allows him to derive the
classical equation directly, by a straight substitution. In doing
so, MM proves that the classical equation is not an approximation
at low speeds, as has always been assumed. It is an exact
equation. The binomial expansion of the differential in gamma
is a manufactured proof, since gamma
itself does not exist as a correct transform in any part of
Special Relativity.
In "An Algebraic Correction to Special Relativity and Refutation of Gamma", Miles Mathis derived new transformation equations for
time, distance and velocity. His central transform there was
α
= alpha
= 1/[ 1 – (v/c)] = 1 + (v'/c), which replaced gamma.
Interestingly, the term that Einstein called alpha is commonly used in optics to transform the frequency of light. MM recently found Richard Feynman using it in a proof of Relativity (Feynman Lectures on Gravitation, lecture 7). So even the status quo should have been surprised to find Einstein using gamma to transform light frequency as he does. No one, apparently, has ever seen the contradiction in this until now.
Before getting to Einstein's thought problem, MM must review
the findings of the previous paper listed above, since they are crucial to
understanding this paper. In that paper MM showed that Einstein
misunderstood his initial coordinate system and variable
assignments, so that his transforms end up being unassignable. He
applies gamma
to his time and distance transforms, in this way:
t = γt'
and x = γx'.
Unfortunately, these transforms are not correct. In his various thought problems—the most famous of which is the man on the train—Einstein has three coordinate systems. He has the man's system, the train's system, and the system of the platform, for example. But he tries to solve from only two systems. In his equations, he has only a primed system and an unprimed system, but no double-primed system. At the end, when he finds t = γt', he has mistaken a transform from the man to the platform for a transform from the train to the platform. Einstein completely ignores the direct transform from the platform to the train.
His given velocity v is
the velocity of the train relative to the platform, he tells us.
But he does not say whether this is the velocity as measured from
the train or from the platform. The two measurements must be
different, but Einstein never includes this difference in his
calculations. t = γt' therefore applies to a transform from
the platform to the man, which is in fact a transform of two
degrees of relativity. He never provides transforms for one
degree of relativity.
t = γt'
should read t = γt''
Einstein's gamma
is incorrect for two degrees of relativity as well.
MM in the previous paper listed above shows that the correct transform is alpha (α) given the transform for the first-degree relativity as:
t = αt' and x = x'/α
MM, having corrected Einstein's first-degree transforms, was the first to offer corrected second-degree transforms, although these do not enter into mass transform solutions.
MM's first-degree transforms are in inverse proportion between x and t, whereas Einstein's were in direct proportion. His mistake came about by borrowing the light equations of Lorentz, x = ct and x' = ct', which MM has shown are incorrect.
Finally, MM's discovery of first-degree transforms allowed MM to derive a first-degree transform for velocity, which Einstein never derived. Einstein's transform for velocity is for two degrees of relativity, v to v'', as he admitted, and it has never been questioned.
Until MM's paper, there had been no v', nor any idea that it was necessary to the solution as it was believed that Relativity is symmetrical around v, but this is false. It could be symmetrical around velocity only if system S was “me measuring you,” while S' was “you measuring me.” But since in Relativity, S' is “me measuring you,” while S is “you measuring you,” the equations cannot be symmetrical. Without this symmetry, we must find two values for velocity from the beginning.
In
this current paper, MM shows that the correct mass transform must
be derived from one degree of relativity, using v'. Einstein was
not capable of this solution, since he did not have a v' in his
choice of variables.
Part One - Einstein's Solutions
In this paper he has a body at rest emit two planes of light in opposite directions. The two planes of light have equal energies; therefore the body remains at rest after the emission. He then asks how the energy of this body before and after the emission would look to an observer moving directly away from the body at velocity v. Einstein lets the two planes of light emit from the body at angles to the x-axis and therefore to the observer.
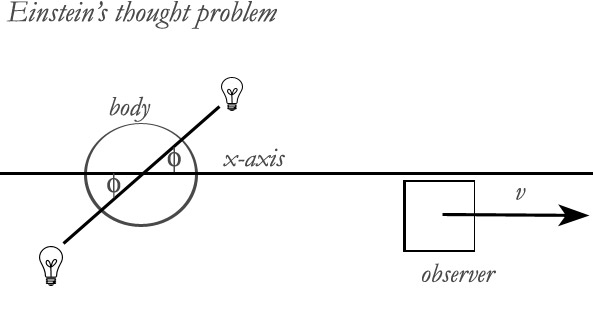
To be precise, he never specifies that the observer is moving away from the body (in the positive x direction, with the body at the origin) but it is implied by analogy to his previous paper. MM will say, in passing, that his failure to specify a direction in this paper has had far-reaching consequences, since it has been assumed (without much argument one way or the other) that the direction is not important. That is, all the transforms of Special Relativity are now assumed to be non-specific regarding direction. This is too bad, since MM has shown (and will show again, below) that Relativity must be specific regarding direction.
Einstein lets the two planes of light emit from the body at angles φ to the x-axis, and therefore to the observer. Let us call B the system of the observer and A the system of the body. Using his nomenclature,
E0 = the initial energy in A. This is not kinetic energy (from the point of view of the emitting body) since he states that the body is not moving in A. It is unclear what E0 is at this point. But from the outcome of the equations, E0 must be what he calls the initial rest energy, as in E0 = m0c2. Since the body is at rest in A, E0 is both the rest energy and the total energy.
E1
is the energy in A after the emission of the two planes of
light.
H0
is the initial energy of the body as seen from B. That is, it is
the initial rest energy plus the kinetic energy.
H1
is the final total energy of the body from B, being the final
rest energy plus the final kinetic energy.
L/2 = the energy of each plane of light, as measured from A.
E0= E1+ L/2 + L/2
This is the equation
as calculated from A
H0= H1 + aL/2 + bL/2
This is the equation from B, where a
is the negative angle transform and b
is the positive angle transform
a
= γ[1 + (v/c)cosφ]
b
= γ[1 - (v/c)cosφ]
where γ= gamma
=1/√[1 - (v2/c2)]
(E0= E1+ L/2 + L/2
Now,
Einstein says the initial kinetic energy of the body is
represented by the equation
K0
= H0
- E0
And
the final kinetic energy is represented by
K1
= H1
- E1
So
that the change in kinetic energy is
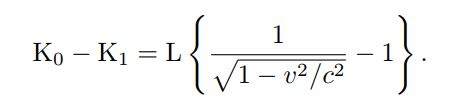
"The kinetic energy of the body with respect to (ξ, η, ζ) diminishes as a result of the emission of light, and the amount of diminution is independent of the properties of the body. Moreover, the difference K0 −K1, like the kinetic energy of the electron
(§10), depends on the velocity.
Neglecting magnitudes of fourth and higher orders we may place"
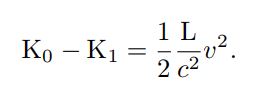
. He concludes: From this equation it directly follows that: "If a body gives off the energy L in the form of radiation, its mass diminishes by L/c2"
(Using the later terminology E for L, m=E/c2 reduces to E=mc2)
That is the whole paper. It takes up less than three pages in Annalen der Physik.
A long discussion of Einstein's mistakes follows:
The cardinal error in this whole derivation is in the final two
steps. At the end Einstein mixes up the last equation with the
next to the last equation, treating them as the same thing. But
one expresses the final kinetic energy and the other expresses
the change in kinetic energy. They are not the same in this
problem, since the body has an initial kinetic energy (from the
point of view of the observer). Einstein assigns the term γL
to H1
and the term L to E1.
He assumes that H1
is mc2
and E1
is m0c2.
But look back up the series of steps:
L ≠ E1 (
H1≠ γL
This is because K1≠ K0- K1.
Once
you have digested the enormity of that, notice that in the final
step Einstein has subtracted the final kinetic energy from the
initial. This is backwards. It is standard practice to subtract
the initial energy from the final to find a change in energy.
Corrected, the equation should read:
K1
- K0
= L(1 - γ)
An even greater error is made in assigning values to the light angle transforms a and b.
Notice that the magnitudes of a and b are not equal. The observer in B would therefore expect Einstein's body to change course, since one of the planes of light would have more energy than the other, measured from B. Einstein ignores this. The body must not change velocity, because then the change in kinetic energy would be due to that velocity change and not to a change in mass—which is of course what he is trying to prove. By a mathematical trick Einstein gets the two planes of light to add to unity in both systems, but in B the two light planes do not have equal energies.
Another crucial error in this thought problem is that Einstein applies his transform γ only to the planes of light, L/2 and L/2. He does not transform the mass, velocity, or energy of the body directly. Those transforms are implications of the thought experiment, but they are calculated indirectly, as results of these very energy equations. In truth, the masses are applied to the energies somewhat willy-nilly, and a rigorous explanation has never yet been provided.
The problem can be solved down from the energy equations, of course, but it is a curious method, especially as it stood (and still stands, until the publication of MM's paper) as the first and only method. To solve from the energy equations one must be extremely careful to keep all the hidden variables in order. Einstein does not do this, as MM shows in the paragraphs that follow. But the greater problem is that solving by this method keeps those variables in the dark. In solving a problem for the first time, a scientist or mathematician should put all the variables in plain view, showing how they are transformed directly. He should not derive them indirectly by a compact but impenetrable method. This problem is the perfect example of that. Einstein has not been corrected for a century due to the obtuseness of his proofs. In MM's opinion, it would have been more helpful to do transforms on the basic variables, those being mass and velocity, and then to build energy equation from those. As it is the conceptual basis for relativistic mass, momentum and kinetic energy has been keep under a cloud from the beginning.
As a first
example of this cloud, notice that if you insert m0c2
into the last equation above, as Einstein did later and as
history still does, this implies that L = m0c2.
Not E0
but L. In the beginning of the equations, E0
is assumed to be the rest energy of the particle. At the end,
Einstein and history have assigned m0c2
to E0.
But according to these equations, L = m0c2.
That is, m0c2
is not the rest energy before or after the emission of the light,
it is the change in rest energy. It is the energy equivalence of
the planes of light.
You may say that the situation is
different when Einstein expressly assigns m0c2
to the rest energy.
(Einstein assigns the variable in question to mc2 not m0c2. He assumes that m stands for the rest mass here, since the electron starts from rest.* Unfortunately, the rest mass changes during the acceleration (which is what he is trying to prove) so that m is not the final rest mass. It is the initial rest mass. This conflicts with later interpretations and assignments of the kinetic energy equation. Regardless, D is not assignable to any mass of the electron.)
In that problem ("Dynamics of the Slowly Accelerated Electron," last part of section 10 of On the Electrodynamics of Moving Bodies, 1905) he applies a force from an electrostatic field, taking the electron from rest to v. There is no L involved.
No, there is not. But the situation is directly analogous, otherwise how could it yield the exact same equation? In it, the electron starts at rest with a given energy. Let us call it E0 again, as above. If we apply all the electric force at the first instant, to complete the analogy to the light planes being emitted, then we can follow the problem in the same way, without calculus.
(Einstein actually uses calculus, and provides us with a single equation: K = ∫ εXdx = m∫ β3vdv. This kind of math is not helpful in creating a new theory, since precisely none of the concepts are enumerated.)
The body reaches v instantaneously, and we want to
know how much energy it has gained from the force. Einstein has
his electron accelerate slowly, but that is only to avoid giving
off radiation. That is, it is an experimental concern, not a
theoretical concern.
D = the energy gained from the electrical
force
E0
= E1
- D
Einstein says the
field imparts a velocity to the electron. So the electron is now
the moving body. Let us assign it to B, the observer being at
rest in A. It is the electron that is moving, not us. It would be
even more precise to say that the electron is B. It is not moving
in B; it is the system B itself.
H0
= H1
- bD
where b
is the transformation term.
But, the electron starts at rest relative to A and B, therefore
H0
= E0
K1
- K0
= H1
- E1
- (H0
- E0)
= H1
- E1
But K0
= 0 since the electron has no kinetic energy at rest in both
systems. So:
K1
= H1
- E1
= H0
+ bD
- (E0
+ D)
K1
= bD
- D
The kinetic energy is equal to the total energy
measured from a distance minus the total energy measured from the
body. And this is the energy taken from the field as measured
from A minus the energy taken from the field as measured by B.
This is precisely equivalent to the example with the light
planes—substituting D for L—except that in one the
body (the electron) is the moving system and is gaining energy,
and in the other the body is the at-rest system and is losing
energy.
Here again, though, if you insert m0c2 as it has been historically into the last equation, you find that it is equal to D, not to E0. D is the energy gained from the field, by Einstein's own variable assignments. E0≠ m0c2.
*Einstein assigns the variable in question (MM's D above) to mc2 not m0c2. He assumes that m stands for the rest mass here, since the electron starts from rest. Unfortunately, the rest mass changes during the acceleration (which is what he is trying to prove) so that m is not the final rest mass. It is the initial rest mass. This conflicts with later interpretations and assignments of the kinetic energy equation. Regardless, D is not assignable to any mass of the electron.
Also notice that, just as in the proofs of Special Relativity, Einstein has failed to assign v to either system A or B. This must affect his calculations. Nor does he consider that kinetic energy can be calculated from either system, A or B. If A can calculate a velocity relative to B, then A can also calculate a kinetic energy. He does not specify where K is measured from. The form of the equations implies that K is measured from B, but this is not a necessity. The fact that Einstein does not carry into this problem a v', as MM does, has had long-reaching consequences.
Einstein still should not have applied it to the light rays here. Physics already had a transform for frequency that had nothing to do with Special Relativity, and that should be applicable in this problem. This transform is f' = f(1 -+ v/c). (This is the Doppler Effect from 1842 where f is the frequency of the wave, v is velocity of the source and c is the velocity of the wave.) Relativity has not overwritten or jettisoned this transform; Richard Feynman actually used it much later as part of his proof of Relativity. (Feynman Lectures on Gravitation, eq. 7.2.1) That is, he uses the correct transform to derive the incorrect one. Current theory is built on a simultaneous and inconsistent use of both transforms.
And finally, gamma is not the transform to use here. Even if gamma had been correct as a transform for distance and time in Special Relativity as MM has shown in "An Algebraic Correction to Special Relativity and Refutation of Gamma". It is incorrect mainly because Einstein never saw the existence of v', from the beginning. And, even if gamma had been correct as a transform for mass and time in Special Relativity, it still should not have been applied to the light rays here. Physics already had a transform for frequency that had nothing to do with Special Relativity. This transform always has been equivalent to MM's basic transform alpha.
Because he does not have enough variables or coordinate systems, Einstein has once again been forced to finesse his math. He has done so in several places, in fact. In the first thought problem, the initial trick is letting L/2 stand for half the emitted light. Splitting his variable so that it yields a two-term equation is done only to ensure that it cancels properly.
The second trick is using a transformation term that has a 1+ and a 1- in the numerator that also cancels out. This is not just luck. Nor is it necessity. As MM will show, it is much more convenient to choose the send the planes of light straight ahead and straight back, since then they are all in the same line as the given v. Everything is then in the x-direction. Why does Einstein choose an angle? He chooses it because it is the best way to finesse this equation. If he lets the planes of light be emitted in a line, he gets into all kinds of trouble.
His split equations won't cancel out in that case, according to his own faulty theory, since Einstein's transforms are the same regardless of direction. In using the angles, as he has, he ensures they cancel, but only at the cost of theoretical consistency. Mathematically they cancel. Conceptually they do not, as MM has shown. The observer in B should see the body change direction, and Einstein cannot explain why this does not happen.
Einstein's equations do not distinguish between movement toward and movement away. He says that moving things act the same, no matter the direction. Therefore the energy of both planes of light should increase from the point of view of B. If the body had sent out electrons instead of planes of light, Einstein would have found both the electron receding and the electron approaching the observer in B to be slowed and mass-increased. But this is false, as will be shown.
Finally,
Einstein finesses the equations by assigning (in the last
equation of either problem) the first term to the kinetic energy
and the second term to the rest energy. Like this,
K0
- K1
=
m0c2
- m0c2}
√[1 -
(v2/c2)]
Einstein
says that the second term (the term on the right) applies to the
rest energy of the particle. There is no reason to do this. It is
an equation with two terms, but the terms are not divisible or
singly assignable without a very compelling reason and a full
explanation. MM has shown that the two terms are simply the
outcome of a finessed equation. There is no necessary physical
reality to either term.
To clarify this, let's look again
at the light-plane problem. At the end Einstein finds that:
K0
- K1
= γL - L
If L =
m0c2
, then what is the value of E0?
Let us see.
E0
= E1
+ L
The initial rest
energy = the final rest energy + the rest energy? This only makes
sense if the final term is understood to be the change in rest
energy. L is actually the mass equivalent of the planes of light.
Even if Einstein's final equation were correct in form (it
isn't), it would imply that m0c2
is the mass equivalent of the light, not of the body. But this is
not what m0c2
means in current energy equations.
Now let's look at the calculus derivation of E = mc2 from a current textbook.
It follows Einstein pretty closely—meaning it makes all the mistakes he makes, and then adds a few of its own. The problem for the textbooks is that they try to clarify some of the things that Einstein purposely kept in the shadows. They try to apply real math to things that Einstein simply glossed over. Unfortunately, they are no more thorough than he was.The
first thing they do is state that they take the Work-energy
Theorem as still valid in Relativity. This is false. It is valid,
but not with the same equations. Remember that Einstein throws
out the classical equation for kinetic energy. In fact, the
textbook finds, at the end of these very equations, that E ≠
mv2/2. But it assumes, for some reason, that the integral based on
this equation is valid!
W = ∫ Fdx = ∫ dpdx/dt = ∫
vdp
But this is absurd, since according to Einstein, energy is not expressed in the same terms in relativity as it is in classical mechanics. The integral ∫ Fdx works because F = ma and v = x/t , etc.
From this they get
W = ∫ dpv - ∫ pdv
but p ≠ mv
in relativity. You can't just juggle the same old variables for a
few steps and then suddenly introduce a mass substitution to make
it all right. But this is what is done.
W = mv2
- ∫
m0v
dv
√[1 - (v2/c2)]
= mv2
+ mc2[1
- (v2/c2)]
- m0c2
and so on
Notice that if we so much as lose the square
root of the gamma
term, then the integration is ruined. You have no third term from
v = 0 as you do in the current integration. So you have no m0c2
term. But it does not matter since the integration was
compromised long before that.
The textbook at hand says this (which is typical): "We
call mc2
the total energy of the body, and we see that the total energy
equals the rest energy plus the kinetic energy."
mc2
= m0c2
+ K
But this assigning of physical realities to the terms in the equations is completely ad hoc, whether it is done by Einstein or the current textbooks. As MM has shown above, the equation works in the same way whether the particle starts from rest or not. In these equations, m0c2 is the change in rest energy, not the initial rest energy or the rest energy at zero. And notice that mc2 has been assigned to the total energy with no mathematical or theoretical proof whatsoever. With the givens we have in Einstein's thought problems, the real mass of the body or electron is not calculable or assignable, beyond the given E0.
Part Two - A Correction for Einstein's Thought Problem
The first thing to do, before deriving new equations for mass increase and energy, is to correct the thought problem MM has just critiqued. Having asserted that Einstein has made mistakes, the problem should be rerun in the right way.
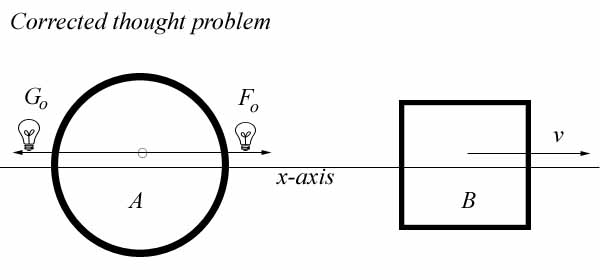
Let us return to the light-plane problem. MM gets rid of the angles of emission, leaving the light to travel only along the x-axis. One plane of light travels directly toward the observer in B, and one plane directly away. Since with light the energy is dependent on the frequency, not the speed, we need linear transforms for frequency, not velocity. The light moving in the +direction of v will be red-shifted, since although it is moving toward the observer in B, the observer is moving away from it. As regards the other plane of light, the case is a bit more subtle. That light is not moving toward the observer at all. It is wrong to say that an object moving away from an observer has a kinetic energy, since that object cannot possibly do any work for the observer. To be even more precise, light moving away from an observer cannot be known to exist at all. However, we can measure the energy of the incoming light, and we can see—or we are given—that the emitting body has not changed speed or direction. Therefore, the receding light must have an equal but opposite energy to the incoming light. This is only an inference though, and may not be measured or seen directly. Let us see if we can express this in equations. MM is assuming the given velocity is B as measured from A.
Einstein's nomenclature is (purposefully) confusing so MM calls the L/2 incoming F0 and the L/2 receding G0.
If F1 is the
energy of the light as measured by B, then
αF1
= F0 since F1 <
F0
F0 = -G0
The energy of a plane of light is dependent only upon its
frequency, since its velocity is always c.
E = hf, where h is
Planck's constant and f is frequency. The transform for frequency
is
f' = αf
Which
makes the transform for the energy of a light plane
E' =
αE
Amazingly, this is the current transform for frequency, as used by scientists for decades. Richard Feynman used it in his explanations of Special Relativity, at the same time that he was corroborating gamma and other mathematical falsehoods. So MM's alpha has been a common transform in optics for several generations. But until now it has not been properly tied to Special Relativity and the mass transforms.
The magnitude
of the energy of G1 must equal F1,
otherwise the observer in B would see the body change velocity or
direction after emission. We are told that it does not change
velocity. It stays at rest in A, and keeps velocity v in B. We
could express the direction of the planes of light as angles of 0
and 180, to mirror Einstein, but notice that it is completely
unnecessary in this sort of problem. We are only interested in
vectors, not in angles. Both planes of light end up being
subtracted from the mass of the body. Einstein's use of 1 + cos
and 1 - cos, etc. was just false bombast. This is the way the
equations should go:
E0 = E1 + F0
- G0
E0 - E1 = 2F0
H0 = H1 + F1 - G1
[We are dealing with energy as a vector,
remember!]
H0 - H1 = 2F0/α
You may say, shouldn't the light plane traveling in the -x direction have a blue shift, and a transform that is the inverse of the red-shift transform? No. Light is blue shifted if it is traveling toward the observer and the observer is traveling toward it (or if the point of emission is traveling toward the observer-which you see is the same thing). A light plane traveling in the -x direction is neither blue-shifted nor red-shifted, nor subject to any possible transformation. It is invisible and undetectable, except by inference.
Now, Einstein says the initial kinetic energy of the body is represented by the equation K0 = H0 - E0
And the final kinetic energy is represented by K1 = H1 - E1
So that
the change in kinetic energy is
K1 - K0
= H1 - E1 - (H0 - E0)
K1
- K0 = -2F0/α + 2F0
Now, if we want to put L back in, and solve, we get
L = 2F0
ΔK
= L[1 - (1/α)]
ΔK = L(v/c)
The body lost
the mass equivalent of the light but gained kinetic energy. This
is simply because the body had a negative kinetic energy to start
with. It was moving away from the observer and therefore could do
no work. Its loss of the energy of the light gave it a smaller
negative kinetic energy, which is of course a positive vector
change.
Einstein had to
finesse his equations to get a positive number at the end. MM has
shown how to analyze the vectors correctly.
You can see
that MM has done a lot of housecleaning. The way MM dealt with the
planes of light was quite different than Einstein. Notice, for
one thing, that one would never let the planes of light be emitted
in any other way than the way MM did. Why? Because any other
planes of light, emitted at any angle to the x-axis, will be
undetectable from B. Einstein assumes that B can perform
transformation equations on light that never even comes to B.
Light emitted at any angle will never reach B, and is therefore
not a source of possible calculation. In that case all energy
changes will be inferences; none will be measurements.
Which would make Einstein's thought problem a fantasy from
beginning to end, rather than a meaningful potential
experiment.
Furthermore, if m0c2 is inserted into the equation, then L = m0c2. In this problem, according to Einstein's own assignments, this is the mass equivalence of the emitted planes of light, not the rest mass of the object.
Finally, MM's corrections
make it clear that L/α cannot be assigned to mc2.
Currently, Einstein's theory assigns m0c2
to L and mc2 to γL (which is MM's L/α). He
says that ET = γL. But this is false, according
to his own variable assignments. From the equations above and
current theory, we have ET = H1 + K = H1
+ γL - L
H1 ≠ L Therefore, ET ≠
γL
Above MM showed that ET ≠ H1. Here MM has shown that ET ≠ γL. The truth is that ET is not singly assignable to any of Einstein's energy variables; nor is it assignable to mc2.
(From MM emc2 gloss)
Part Two (B) - the Redrawing Corrections
Now let us correct these errors. We will have to change the thought experiment a bit in order to produce all the clear and definable variables we need. Let us start with the body and the observer both at rest together. Let us have the body emit only one light ray in one direction, and let us limit this ray to a single photon. What difference will this make? Einstein rigged his math so that his body did not change position in system A or velocity in B. Our new body, however, does change velocity. It goes from rest to a final velocity of v' as measured from itself in A, or from rest to v measured from the observer in B. Einstein's two planes of light cancel out. MM's one photon has no twin in the opposite direction, therefore our body is given a push and it achieves a velocity.
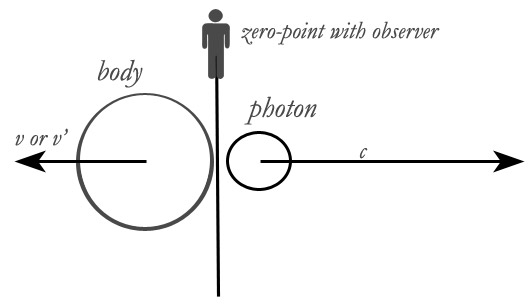
It is true that this new thought problem implies an acceleration over an interval, but we can get around that by using an average velocity over that interval. Let us first relist our variables, using Einstein's as a guide.
E0 = initial energy of the body (measured by the body) before emission of the photon.
E1 = total energy of the body measured by the body after the emission of the photon.
H0 = initial total energy of the body as seen from the observer.
H1 = final total energy of the body as seen from the observer.
F0 = energy of the photon as measured by the body
F1 = energy of the photon as measured by the observer
α = light frequency transform
F1 = αF0 since F1 > F0
E1 = E0 - F0
H1 = H0 - F1
E0 = H0 since the body is initially at rest in both systems, A and B
H1 – H0 = -F1 = -αF0
And the final kinetic energy is represented by
K = H1 – E1
= H1 – (E0 - F0)
= H1 – (H0 - F0)
= -αF0 + F0
K = (1 – α)F0
Now that Einstein's problem has been brought into line with MM's thought problem, MM may use F1 as the energy of MM's photon. Furthermore, MM may assume that F1 = m0c2. If we assume that light can have a mass equivalence, then from the equation for the momentum of light we have
E/c = m0v
E = m0c2
where m0 is the mass equivalence of the light. [Notice that MM is accepting Einstein's postulates concerning mass and energy equivalence; MM is simply not accepting his math. To achieve E = m0c2 we do not need any of Einstein's math; we only need the momentum equation for light and the postulate that light has a mass equivalence—both of which Einstein explicitly accepted.]
In order to proceed, we need an equation for α. MM's new thought problem shows us that we need two measurements of mass and two measurements of velocity. That means we need two more variables than Einstein worked with. We need m, m', v, and v'. This is the only possible way we can do logical mass and velocity transforms. MM must import the equations for v and v' from MM's first paper on Special Relativity. MM will include here a gloss of the math used to achieve them. In these equations, primed variables are as observed by A (the object itself); unprimed variables are as observed by B (the observer). A simple correction to Einstein's parameters gives us
xt = x't'
v = x'/t = x/t' ≠ x/t
v' = x'/t'
The reason v ≠ x/t is that these unprimed variables must be defined as variables as observed by B, not in B. To say that another way, x is how x' looks to the observer. It is not how the observer sees his own distances. This is a huge difference, and it is the main problem of Einstein's and Lorentz's original variable assignments. The variable x is a distance in A observed by B. It is not a distance in B observed by B. You must understand this fully before you can proceed with any of MM's corrections.
t = t' + (x'/c)
= t' + (v't'/c) = t' (1 + v'/c) = t'/( 1 - v/c)
v = x'/[t'(1 + v'/c)]
v = v'
1 + (v'/c)
v' = v = α v
1 - (v/c)
α = alpha = 1/[1- (v/c)] = 1 + (v'/c) = c/(c - v) = (c + v')/c
Alpha is the current term for light frequency transform, as said above. MM has shown that it is also the correct term for one-degree velocity transform, replacing the term gamma in the first part of Special Relativity.
Now we can continue with our energy transforms. Next we need mass transform equations. These are as simple to derive as the velocity transforms. When the body emits the photon it must recoil, achieving a velocity. This velocity can be found by using the conservation of momentum—the momentum of the light must be equal to the momentum of the ball:
mvav' = m'v'av = E/c = m0c
m = m0c/vav
m0 = m(vav /c)
v'av = αvav = mvav/m'
m = αm'
1/α =1 – (2vav/c)
We assume a constant acceleration over the interval in question, so that the average velocity must be half the final velocity, so
vav/c = [1 – (1/α)]/2
mvav/c = [m – (m/α)]/2
m0 = (m – m')/2
And from above we had these equations:
K = (1 - α)F0
F0 = m0c2/α
K = -(v/c)m0c2
So now we have almost enough to solve. But remember that m0 is not the rest mass of our body in question; it is the mass equivalence of the emitted photon. We need to solve in terms of the body's mass, not the photon's mass. To do this, we need another mass variable beyond the ones above. It turns out that there are several variations of mass increase and decrease, and the equations vary a bit depending on whether the bodies are emitting or absorbing and whether they are moving toward or away from an observer.You will have to consult MM's longer paper (An Algebraic Correction to Special Relativity) to see why this is so. But you may notice that in Einstein's thought problem, the body would be measuring the normal frequency of light and the observer would be measuring a redshift. His observer is moving away from the point of emission. But in MM's thought problem, the observer is at the point of emission already. It is the body that measures the redshift.
By definition–both MM's and Einstein's–the rest mass of the body is the moving mass minus the mass equivalence gained by moving. In this problem, the mass equivalence gained by moving can only be the mass equivalence of the ejected photon. What the body lost in the photon it gained in movement. But we have two moving masses, m and m'. We also have two possible mass equivalences for the photon, since A and B will get different numbers for its energy (F0 and F1). We must choose m' since it is connected to v', which is the correct velocity (MM has shown that v and m, although calculable, are not correct since they have been skewed by c). Likewise, we must choose F1 since it is connected to the normal frequency of light. It gives us the correct mass equivalence of the light. MM has defined the normal frequency of light as the frequency measured from any point at rest relative to the point of emission.
| mr = m' - m0 m0 = [m – (mr + m0)]/2 3m0 = m – mr K = -(m – mr)(v/3c)c2 -3cK/v = mc2 – mrc2 express mr in terms of m multiply both sides by v2/c2 The kinetic energy is negative in MM's problem because the body is moving away from the observer. It can do no possible work on the observer. |
Once Einstein's variable assignments are corrected it turns out that the classical equation is precisely correct, meaning that it gives us exactly the same numbers that relativistic equations give us. Einstein and current wisdom both treat the classical equation as an approximation at slow speeds relative to c. As supposed proof of this, they expand the square root in gamma using the binomial expansion, the first uncancelled term being v2/2c2. But this is once again a fortuitous collision of luck and bad math. MM has shown that gamma is an incorrect transformation term, so that expanding the square root of the term is pointless. If there is no gamma, there can be no expansion of the square root and no proof of the approximation of mv2/2. Besides, this expansion proposes to find that
K ≈ mrv2/2
Which is absurd. What should have been intended is to show that
K ≈ mv2/2 at slow speeds
This latter equation is the classical expression of kinetic energy. As MM has shown, expressing kinetic energy in terms of a rest mass in a classical equation isn't even sensible, once it is understood what the different terms mean.You can't express kinetic energy in terms of a rest mass, in a classical equation. The mass variable in Newton's equation must be a moving mass. The relativistic equation would have to resolve to either mv2/2 or m'v'2/2 at slow speeds, even if gamma and Einstein's theory were correct. Having it resolve to mrv2/2 is just further proof that no one knew what was going on with the math and the variable assignments.
Now let us derive the new energy transforms. Above we found that
-3cK/v = mc2 – mrc2
-K ≠ mc2 – mrc2
Which means that if the total energy,
ET = K + mrc2
ET ≠ mc2
m' = m[1 - (2vav/c)]
mr = m[1 - (2vav/c)] – m(vav/c)
= m[1 - (2vav/c) – (vav/c)]
mr = m[1 - (3vav/c)]
beta = β = 1/[1 - (3vav/c)]
ET = mrc2 - (v/c)m0c2 = mc2/β - (v/2c)c2 [m – (m/α)]
= mc2/β - (v/2c)[mc2 – (mc2/α = mc2[(1/β) - (v/2c) + (v/2αc)]
ET = mc2[1 – (3v/2c) – (v2/2c2)]
Now let us find ET in terms of mr, so that we can compare the transform to gamma.
ET = mrc2 - (v/c)m0c2
mr = m' - m0
m0 = mrβ/α - mr
ET = mrc2 - {mr(v/c)c2[(β/α) – 1}
= mrc2 - {mr(v/c)c2[v/(2c – 3v)
ET = mrc2{1 – [v2/(2c2– 3cv)]}
K = mrc2{1 – [v2/(2c2– 3cv)]} – mrc2
The transformation term here is 1 – [v2/(2c2– 3cv)], which is not gamma. In his paper An Algebraic Correction to Special Relativity, MM shows that there are several variations of this transformation term. For example, the solution to Einstein's original thought problem gives us the transformation term 1 + [v2/(2c2– 3cv)], which is also not gamma. A body moving toward an observer would have the term 1 + [v2/(2c2 + cv)].
In his paper An Algebraic Correction to Special Relativity. MM showed that Einstein's own thought problem also resolved to the classical equation. All the various problems MM solved resolved to K = ±mv2/2. Amazingly, this was the one constant, no matter what variations of energy transformation that was dealt with.
(End of MM emc2 gloss that skips to The Accelerator Problem -Why 108?)Part Three - Thought Experiment 3
Since Einstein's method for deriving mass increase equations has been thrown on, MM must now derive them on MM's own, using MM's own thought problems.
Let us say that we have a tiny ball containing a device that emits light. It is able to emit light one photon at a time, with a known energy. At a distance of 300,000km from this ball is a mirror that reflects directly back to the ball. This distance has been measured locally (by walking it, say). It is a given, not a measurement by the ball after emission. Also, the zero-point of the experiment is marked on the ground with a white line, so that an observer may be placed there.
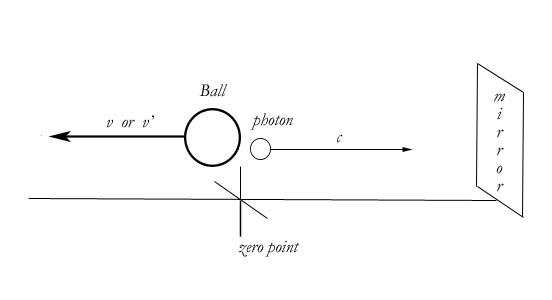
We run the experiment twice. The first time the device in the ball emits a photon toward the mirror at T' = 0s, and then receives the same photon upon its return from the mirror (it does not re-absorb the photon, it simply measures it with an instrument). T' is the time on the ball's clock. At the beginning of the experiment, just before the emission of the photons, T' = T. That is, the clocks of the zero point and the ball are synchronized.
The second time, the device emits a photon at T' = 0s, another at T' = 1s, and then another at T' = 2s. The observer at the zero-point intercepts the second and third photons from the ball in order to calculate where the ball is after T' = T = 0. This observer also intercepts the first photon returning from the mirror.
By the conservation of momentum, the ball must recoil in the
opposite direction from the emission of the photon. When the
photon returns, the distance the ball has traveled may be
measured, and the inertial mass of the ball may be determined.
Question: will the mass of the ball as calculated from
the ball be equivalent to the mass of the ball as calculated from
the zero point of the experiment? If not, how will they differ?
L
= distance from zero-point to mirror
E = energy of photon = 1
x 10-19J (say)
m' = mass of ball, measured by the
ball
v' = velocity of ball, measured from the ball
Let us calculate from the ball, first of all. In this case, the ball is the measurer, and the system of the ball is therefore the S' system—the primed system (MM makes the local system the primed system simply to be consistent with MM's other paper). What does the ball see?
The simplest thing to do is to let the photon return all the way to the ball. We could let the photon return to the zero-point and then let a signal be triggered, but that seems redundant, since the signal would have to be a light signal.
Let the ball be very tiny, to be sure it travels a nice long
distance. But do not assume it reaches velocity instantaneously
(this will be important later). When the photon arrives back at
the ball, the ball looks at its clock and discovers that 2.5
seconds have elapsed. The ball thinks, "This is very easy.
The light took one second to get over to the mirror and one
second to get back, and half a second to reach me. If the mirror
is 300,000km from the zero-point, then MM is 150,000km from the
zero-point. MM went that far in 2.5s, therefore MM's average
velocity (relative to the system of the zero-point) is:
v'av
= 150,000km/2.5s = 60,000km/s
By the conservation of momentum, the momentum of the light must
be equal to the momentum of the ball:
E/c = m'v'av
m'
= E/cv'av = 1 x 10-19J/(3 x 108m/s)(6
x 107m/s)
=
5.55 x 10-36kg
Now let us calculate from the
zero-point. The first photon arrives at the zero-point in 2
seconds, according to the clock at the zero-point. The observer
at the zero-point then must measure the distance the ball has
appeared to travel. The observer does this by receiving the other
photons from the ball. We could use the t-equation from MM's
previous paper, to calculate the difference between the period of
the ball and the period of the zero-point. This would be the most
direct way to calculate, since the only data the zero-point is
receiving from the ball is ticks. [The zero-point is able to
calculate velocity simply from receiving ticks, since the
zero-point knows the local period of the ball. When the ball was
at rest at the zero-point, at the beginning of the experiment,
it's period was 1s.] However, since we have already calculated
the velocity of the ball according to the ball,this step is skipped and MM's velocity transformation equation is used
instead. If the ball calculates its own velocity to be
60,000km/s, then the observer at the zero point will calculate
(by receiving ticks) the velocity to be:
t = t' + x'/c
t'
is a given as 1s. t is incoming data. Therefore x' and v' and v
may be calculated.
v =
v'
1 + (v'/c)
vav =
v'av
1 + (2v'av/c)
vav =
6 x 104km/s
1 + (12 x 104/3 x 105)
= 42,857km/s
(Again, the zero-point could have arrived at
this number without knowing v'av. This is of some
importance below.)
m = E/cvav
= 7.77 x 10-36kg
The mass of the ball has
appeared to increase, if measured from the zero-point, as
compared to measurement from the ball itself. This much is
consistent with the findings of Einstein: mass appears to
increase as time dilates. But the transformation term is
obviously different. MM has used a variation of MM's velocity term
alpha rather than gamma.
Now, one may ask,
which mass is correct? The mass measured from the zero-point or
the mass measured from the ball? Either mass conserves momentum,
as long as we keep it in its own equation. But you can see that
the mass as calculated by the ball itself must be the correct
moving mass, since it is connected to the correct velocity. The
zero-point calculates a larger mass only because it has used an
incorrect velocity. Its visual data has been skewed by time
dilation, making the velocity wrong and then the mass.
Next,
one may ask, what was the rest mass in this problem? Well, there
must be three calculable rest masses: the rest mass before the
emission and two rest masses after (the ball and the zero-point
will calculate different rest masses, unfortunately).
mrB
= rest mass of the ball, before emission
mrAB =
rest mass of the ball calculated by the ball, after emission
mrAZ
= rest mass of the ball calculated by the zero-point, after
emission
m0B = mass equivalence of the photon, as
measured by the ball
m0Z = mass equivalence of the
photon, as measured by the zero-point
The photon will have two mass equivalents, since the photon will
have a different energy relative to the ball than it will have
relative to the zero-point. The ball is moving away from the
photon when the photon returns, so that its energy will be
redshifted. E'< E.
E = m0Zc2 = the
energy of the photon relative to the zero-point
E' = m0Bc2
= the energy of the photon relative to the ball
mrAB=
mrB - m0B
We can solve since we also know that mvav = m'vav'
= E/c
m = m0Zc/vav
m0Z =
m(vav/c)
m0Z = (m - m')/2
= 1.11 x 10-36kg
which agrees with our given value for its energy.
m0Z
= αm0B
m0B = 7.9 x 10-37kg
Now all we need is the rest mass. Some will think that is just the mass measured by the ball, since that is the only mass that is truly at rest with regard to its background. But the ball, using the equation above, is calculating with redshifted light. This means that its value for the mass equivalence of the photon is incorrect. In this way MM's thought problem is not like that of Einstein. In the light planes problem, the body is at rest and the observer is moving away. Therefore the body measures the normal frequency and the observer sees a redshift. But in MM's thought problem, the observer at the zero-point sees the normal frequency and the ball sees the redshift.
Upon emission the ball lost a certain amount of energy. This amount of energy is expressed by E, not by E'. Therefore, the rest mass relative to the zero-point must be calculated with E. This is simply because we must imagine that the ball was not moving at the instant of emission. The ball did not start moving until the instant after T0. Emission took place at T0 , therefore the light has its normal frequency relative to the zero-point.
This seems somewhat strange at first, since the ball is not at rest relative to the zero-point. How can we calculate a rest mass for it relative to the zero-point; and what is more, why would we want to? We want to in order to get the correct energy equations. If we work with the wrong rest mass, we will get the wrong equations. We must use the rest mass that is at rest relative to the light. That is the only true rest mass, in any problem whatsoever. You will say, "doesn't Relativity imply that all bodies are at rest relative to light, since light travels c relative to all bodies?" Relativity does say that light travels c relative to all bodies, and it is correct to do so; however, it is quite obvious that a body that is measuring red or blueshifted light is not at rest relative to that light. The true rest mass of any body will be calculated from unshifted light—that is to say, light with a normal frequency (see a full definition of "normal frequency" below).
And so, in this particular problem, MM must seek the rest mass
relative to the zero-point. How can it be found, since there is no equation for it yet? All that one needs is a mass after emission from
which to subtract MM's photon from. There are two masses, m and m',
but m' is the correct mass since it is connected to the correct
velocity. The variable v' was measured locally, meaning that the
t variable did not need to be transformed. That makes m' a
reliable mass. But it is not the rest mass itself. It is a moving
mass. To find the rest mass, we simply subtract the mass
equivalence of the photon from m'.
mrAZ = m' - m0Z
= 4.44 x 10-36kg
The rest mass before emission is just the photon added back
in:
mrB = 5.55 x 10-36kg = m'
Whenever speaking of rest mass from now on (concerning this
problem with the ball) MM will be talking about mrAZ,
but the notation can be simplified, taking it back to mr.
We should take note that all these masses were calculated
from an average velocity over the interval of acceleration up to
a final velocity. If we had used a final velocity, we would have
found a mass equivalence for the photon that was twice too
little. This final velocity is not used in the mass or momentum
transforms; but it will be used in the energy transforms, simply
in order to be sure to derive equations that are analogous to
the ones that are currently used. The current energy equations
are used given a final velocity. In many experimental situations,
the scientist does not know or is not concerned with how the
particle reached velocity. His or her only data is a final
velocity.*
Some might
complain that the ball must use m0B since that is the
mass it would calculate from the frequency of light it actually
sees. But since we have as one of our givens the fact that the
ball knows it is moving and is already calculating a velocity for
itself relative to the background of the zero-point, it is not
difficult to require that the ball notice that the normal
frequency of light is f rather than f'.
Both the observer
at the zero-point and the ball itself are calculating a moving
mass when they use a momentum equation, since the momentum
equation includes a velocity. The variable m' could hardly be
understood as a rest mass, since it was calculated from an
equation that describes movement.
Using other methods than this experiment (such as a gravitational method), the zero-point would have found the rest mass of the ball to be 5.55 x 10-36kg, before the experiment. It then would have calculated the moving mass to be 7.77 x 10-36kg, from an experiment like this one—a mass that would appear to be confirmed by any subsequent collision of the ball, since the momentum equation used by the zero-point would be assumed to be correct. The momentum would in fact be correct, but neither the velocity nor the mass would be.
Some may want to calculate a momentum using mr, to
find that the ball also miscalculated its velocity. p = mrvr.
But this cannot be done. A rest mass is at rest, by definition,
and can have neither velocity nor momentum nor kinetic energy.
The rest mass is defined as the mass at rest relative to the
normal frequency of light.
As you can see, the momentum
is the same measured from either the ball or the zero-point,
which is just as it must be: mvav = m'v'av.
It could hardly be otherwise, since the masses were calculated
from a momentum equation in the first place. All we have had to
do is keep our variables in order, so that we understand
precisely what we have been given and what we are seeking in each
event and with each solution.
Finally, let me address the
comment that E/c = m'v'av cannot be the correct
equation describing the initial situation, since the ball will
not receive the photon back from the mirror at energy E. It is
true that when the first photon returns to the ball its frequency
will have changed, due to the movement of the ball. Because E =
hf, the ball will receive the photon at E', not at E, and E'<
E.
However, we do not
use E' in this equation for this reason: we are not concerned
with the energy the photon has when it returns to the ball, not
from any vantage; we are concerned with the energy the photon has
when it leaves the ball. The equation E/c = m'v'av
describes an equality of numbers, when all the numbers are
relative to the same background. This background is the
background of the zero-point, or the background of the ball
before it gained a velocity. You may say, no, the variables as
measured against that background are unprimed variables, by
definition. The primed variables as said are measured from
the ball. However, if you think this, you are not being rigorous
enough in your variable assignments. Just as in MM's first paper,
the variable assignments here are very subtle, and we now must
write them out in full, to avoid confusion.
v' is the velocity
of the ball relative to the zero-point, as measured from the
ball.
v is the velocity of the ball relative to the
zero-point, as measured from the zero-point.
There is no
velocity of the ball measured by the ball, relative to the ball.
In the same way, E' is not just the energy as measured by the
ball, it is the energy of the returning photon relative to the
ball. It is not the energy we want for any of our equations.
Both velocity
measurements above have the same background. Therefore in the
equation E/c = m'v'av, E must also be measured against
this background. E must be the original given energy of the
photon.
Before we continue, MM make one final
comment regarding this problem. We have just seen that light may
have a different frequency depending upon who measures it. Of
course this is not news: we have known of redshifts for decades.
But our experiment above has shown us that frequency may be
privileged just as certain measurements of
velocity and mass are privileged here. What is the privileged measurement of light?
The measured frequency of light is normal, and therefore
privileged, when the system that measures the ray or photon is at
rest relative to the point of emission. That is fairly
straightforward, besides appealing to common sense. This
effectively privileges the point of emission of light regarding
measurement of the light's frequency. Notice it is just the
opposite of the privileging of time, velocity and mass to the
local system. Local time cannot be wrong. But the measurement of
the frequency of light can be wrong, from what we have heretofore
called a local system. The ball was the local system above, but
it would have measured f', which is not the normal frequency.
If you say, we can't privilege certain fields like
that—how can we know if we are moving relative to the light
source? But we can't always know. But it is possible to
know in certain situations, from spectra shifts. The fact that it
is possible to know means that there is a pre-existing fact.
Light does have a normal frequency. For instance, we know, due to
stability, that the sun is not moving relative to us. It is
neither approaching the earth, nor fleeing it. Therefore
measurements of the frequencies of sunlight from the earth are
privileged. Notice, however, that measurements of sunlight from
the sun are not privileged, since the sun is moving through
space. You will say, it doesn't matter, since the sunlight is
moving away from the sun, and is therefore undetectable from the
sun. But sunlight reflected back to the sun could be measured
from the sun. [See MM's
paper on the mirror experiment to replace Michelson/Morley].
Part Four - New Mass Transforms
These
then are the new mass transform equations, for one degree of
relativity, if the object is moving away from the measurer.
[alpha must be modified if the object is moving toward the
measurer—see below for modification process; or see paper
on velocity transforms for full proof of modification.]
mvav
= m'v'av
mv'av /[1 + (2v'av/c)]
= m'v'av
m = m'[1 + (2v'av/c)] = m'α
where m' is local mass and m is measured from a distance
What
if we want to use vav instead of v'av?
m
= m'/[1 - (2vav/c)] = m'α
However, these
equations tell only part of the story, as the above thought
problem made clear. The observer at the zero-point would
calculate the ball to have a moving mass of
m'/[1 -
(2vav/c)]
but if the ball subsequently came to rest
relative to that observer and was weighed by him, it would weigh
mr = m' - m0Z
m0Z =
m(vav/c)
mr = m' - m(vav/c)
m'
= m[1 - (2vav/c)]
mr = m[1 - (2vav/c)]
- m(vav/c)
= m[1 - (2vav/c) - (vav/c)]
mr
= m[1 - (3vav/c)]
m = mr/[1 -
(3vav/c)]
| MM calls this mass transform beta. beta = β = 1/[1 - (3vav/c)] |
This is a very
important equation, since it mirrors many experimental
situations. Already you can see that there are many equations
involved with mass increase, and the correct one must be chosen
for the situation. Just as with velocity, we must take into
account the direction of relative motion. In addition, we must
take into account which mass we are seeking, which mass or
momentum we are given, and precisely what we are transforming to
and from.
In the thought problem we have just solved, the
mass changed twice, for two reasons: firstly, it changed because
the ball emitted a photon. This changed the mass even from the
point of view of the ball, of course. So this is not a
consideration of Relativity. Secondly, it changed from the point
of view of the observer, since a velocity was involved. This
second change required a mass transform due to Relativity.
The first change of mass was not a concern of Special Relativity, meaning it was a mass change that could be (and was) calculated without Relativity Transforms.
Part Five - Find Equations for a Velocity Change that is not from zero.
Now let us find equations for a velocity change that is not from zero. Let us imagine an even simpler situation. Let us say that a ball of local mass m' starts out with a local velocity of v1' and ends with a local velocity of v2'. Will its mass appear to increase from a distance? Let us assume (at first) that its local mass will not change, since no particle is being emitted in order to accomplish a higher velocity, as with the photon emission above. First we must specify a direction. Let us say it is moving directly toward an observer or a zero-point. In this case we will not have to make the velocity or the momentum negative. For notice that once we start talking about momentum and kinetic energy, we must think in terms of vectors. Objects moving away will have negative momenta and negative kinetic energies.
Now let us take a closer look at these givens. Are they possible? Is it possible for a ball to change velocity without changing its total energy? Of course not. But can it change total energy without changing its local mass? That is a subtler question. As we saw above, the ball gained a velocity by emitting a photon. Its rest mass therefore changed. In many other situations, especially in particle physics, the local or rest mass of the body in question will be affected by a field or by bombardment, since photons or positrons or neutrinos or other small particles will be emitted or absorbed. It may be that no transfer of energy is possible, even on the macro-level, without a change in mass. However, we will assume that some transfers are totally elastic (nothing sticks or is emitted). At the macro-level this will always be an approximation (although often negligible); at the micro-level it will likely always be a falsification. But for this part of the problem, we will assume that the ball changes velocity without changing its rest mass or local mass.
The initial momentum of the ball as measured by the ball is given by the equation m'v1' and its final momentum by m'v2'.
But in
an experiment where energy or momentum is the yield, then the
mass will be calculated down from the momentum equation. In this
case, the velocity will be measured from a distance, obviously.
Scientists do not measure the local velocity of quanta, or
anything else. So these scientists will be using these equations
for the initial momentum and the final momentum:
pi
= mivi where the
i stands for initial
pf = mfvf
" final
Since there is only one energy output at collision, no matter
where it is measured from
mivi =
m'v1'
mfvf = m'v2'
v'
= v/(1 + v/c)
v1' = vi/(1 + vi/c)
v2'
= vf/(1 + vf/c)
m' = mfvf/v2'
mivi
= v1'mfvf /v2'
mi/mf
= vf/(1 + vi/c)//vf/(1 +
vf/c)
= (1 + vf/c)/(1 + vi/c)
mf
= mi (1 + vi/c)/(1 + vf/c) =
mi(c + vi)/(c + vf)
If
the final velocity is greater than the initial velocity, the
final mass must be less than the initial mass. For an approaching
object, there is an apparent mass decrease. Obviously this is
just to keep the momentum the same. If you are measuring its
velocity and getting a number that is too high (compared to the
real value) then you must measure the mass to be too low, so that
when it hits you, the real momentum and your calculated momentum
are the same thing. If the object were moving away, then you
would once again calculate a mass increase.
And there is your mass transform. It has two v's, unlike Einstein's equation; and this is very convenient, since it allows us to calculate from initial to final.
Now let's see if MM's term causes more change than Einstein or
less.
If vi = c/4 and vf = c/2
then
gamma = 1.03
MM's term = 1.2
Somewhat greater
change in mass.
What if the initial velocity is zero?
If
vi = 0, then mf = mi /[1 +
(vf/c)] = mi/(c + vf)
Of
course, in the same way we can derive a transformation from local
velocities, if we want.
vi = v1'/[1 -
(v1'/c)]
vf = v2'/[1 -
(v2'/c)]
mivi = v1'mfvf
/v2'
mf = mi(1
-v2'/c)
1 - v1'/c
You may be surprised to find that the
body can calculate its own mass increase due to velocity. But if
it can calculate its own velocity, it can calculate its own mass
increase. The body itself would of course interpret this not as a
real change in mass, but as a change in mass equivalence relative
to its background. The body, for itself, has not gained mass but
kinetic energy. The classical interpretation would be that this
is kinetic energy and nothing else. The modern interpretation is
that mass is a sort of energy, especially in a momentum equation,
so that they may be lumped together. MM prefers to think of the
measurement of mass from the object itself as the moving mass.
The object must then do further calculations to obtain its own
rest mass.
The question is, can we also use these
equations to transform from a local mass at rest to a relative
mass at velocity? Let us set the initial velocity to zero, in
which case the initial mass in the relative system should equal
to the local mass or rest mass. mi = m0. We
know this not from the momentum equations, but by definition. In
which case
mf = mr/(1 + vf/c)
This
is only if the object is moving toward the observer, since we
simplified an equation from that problem. The mass variables
would switch if the object were moving away:
(Eq. 1) mr
= mf[1 - (vf/c)]
However, we now have
two equations for the same situation, and they don't match. Even
if we switch directions, the equation we found above isn't
equivalent:
(Eq. 2) mr = m[1 - (3vav/c)]
How can we explain this? It is because the experimental situations aren't the same. In the first thought problem, the ball emits a photon in order to reach velocity. In the second, it doesn't. Notice that the ball has borrowed the energy of the photon in the first experiment. A scientist wouldn't necessarily know this, if he came upon the ball after emission, but it is an important fact of the equations. In the second experiment we are just imagining that the object goes from rest to a final velocity, and we calculate the mass increase due to that velocity. But again it might be asked, is this possible? Can an object gain or lose velocity without borrowing the energy of another object, by collision, emission, or other method? MM does not think so. In any experimental situation, we must assume that any object under consideration—that is not at rest relative to our field—gained its velocity by some means external to our initial measurement. We may postulate emission, collision, or the influence of a field, but we may not postulate a relative velocity that was gained without energy transfer. Therefore, MM hypothesize that eq. 2 is always the correct one.
This equation implies some rather shocking things, of course. The most important being that there is a limit at .5c for v. The mass m becomes infinite when v = .5c. But this is the same limit for v that MM found with his velocity transforms. [There is not really a limit for v' in MM's velocity transforms, but when v' = c, v = .5c. When v' is infinite, v = c.] So at least MM's equations are consistent. Whether this can reconciled with the findings of particle physics is yet to be seen (below).
One thing that makes it slightly easier to accept is that MM is
not postulating a real mass approaching infinity. m is not a real
mass. It is a measurement. MM is postulating a measurement to
approach infinity. Therefore, there is a limit to measurement;
but the variable m does not apply to the real mass at all.
Part Six - Einstein's Momentum Transformation Equation
According to MM's equations, momentum does not need to be
transformed. In order to find our initial transforms for mass, we
had to assume that the momentum of our object from the zero-point
was equal to the momentum measured from the object itself.
p'
= p
m'vav' = mvav
We could not have found a mass transform otherwise. Notice that Einstein, despite never making this assumption, arrives at the same basic substitution as MM. His transform for mass is the same as his transform for time and length, gamma. MM's transform is also unchanged. MM's transform for mass is the same as it was for time, distance and velocity: alpha. But Einstein does not work in the direction MM does. MM used his transform for velocity to find the mass transform. Einstein, who assumes he has no velocity transform in the same situation, must instead develop an energy transform first. Remember that in the light plane problem, he had no v'. So he finds an energy equation and solves down from there to find mass transforms and then a momentum equation.
Like me, Einstein does
not have a momentum transform equation. For Einstein, momentum
can only be calculated by an observer (since he failed to
remember that an object can calculate its own velocity). For
Einstein,
m'vav' cannot equal mvav,
since Einstein has no v'.
Instead, he finds that
p = mv =
γm0v
This is the current equation. In it gamma is understood to be transforming the mass. There is no v' to transform. This is the major problem with the current momentum equation. It proposes to transform from one coordinate system to another, but it does so without transforming the velocity. That is to say, this equation assumes that v is correct-that it is unaffected by relativity. Einstein is transforming m0 (which is in the coordinate system that is going v) to the coordinate system of the observer (which is the unprimed system here). The unprimed system is the system of the scientist measuring the particle whizzing by. But Einstein does not transform the velocity. He finds a velocity transform in Special Relativity, but he does not use it in the momentum equation. Why? One must suppose it is because the velocity transform he finds there is for two degrees of relativity, and he does not think it applies in this situation. MM has shown in his previous paper that it does apply. The given velocity v is affected by relativity and must be transformed. It is affected by the speed of light. Why would the speed of light affect mass but not velocity, requiring a mass transform but no velocity transform?
Einstein's m0 is equivalent in math and theory to MM's
mr. Therefore his equation for momentum is equivalent
to this
p = xmrvav
what does x equal,
using MM's transformation terms?
p = mvav
x =
m/mr = α
p = αmrvav
In MM's theory, this last equation is not a momentum
transformation. It is not transforming from one coordinate system
to another. It is simply expressing the momentum in terms of a
rest mass. The relativity transforms are between m and m'.
Technically you cannot calculate a momentum from a rest mass,
since a rest mass is not moving. But if, for some theoretical
reason, you want to express momentum in terms of rest mass, this
is the equation you should use.
Part Seven - Energy Transformation Equations
Let us now return to MM's correction of Einstein's energy equations and see if we can apply them to MM's problem with the ball and the photon.
First, notice that Einstein's thought problem is analogous to MM's except for one thing. Upon emission of the planes of light, his body does not change position in system A or velocity in B. MM's ball, however, does change velocity. It goes from rest at the zero-point to a final velocity of v' as measured from the ball or v measured from the zero-point. Einstein's two planes of light cancel out. MM's one photon has no twin in the opposite direction, therefore the ball is given a push and it achieves a velocity. In this way MM's ball is more like Einstein's slowly accelerated electron. So we only need to return to Einstein's equations to make the proper corrections.
E0 = the initial energy of the ball (measured by the ball) before emission of the photon.
E1 = the total energy of the ball measured by the ball after the emission of the photon.
H0 = the initial total energy of the ball as seen from the zero-point.
H1 = the final total energy of the ball as seen from the zero-point.
F0 = the energy of the photon as measured by the ball
F1 = the energy of the photon as measured by the
zero-point
F1 = αF0
since F1 > F0
E1 = E0
- F0
H1 = H0 - F1
E0 = H0 since
the ball is initially at rest in both systems, A and B
H1
- H0 = -F1 = -αF0
And
the final kinetic energy is represented by
K = H1 -
E1
= H1 - (E0
- F0)
= H1 -
(H0 - F0)
=
-αF0 + F0
= (1 - α)F0
(The initial kinetic energy was
zero.)
K = F0{1- [1 + (v'/c)] }
= -F0(v'/c)
MM's kinetic energy is negative. It
is negative because the ball is moving away from the zero-point.
It can do no work upon a body positioned at the zero-point. To do
+K amount of work on the zero-point, a force would have to be
applied to the ball creating energy in the amount of 2K. In other
words, a force sufficient to turn the ball around and give it v'
in the opposite direction.
Having brought Einstein's problem into line with MM's own
thought problem, MM may use F1 as the energy of MM's
photon. F1 = m0Zc2 (though I
will drop the "z" after this).
We do not need Einstein's derivation of m0c2
here, nor the textbook's simplified calculus derivation. MM has
shown that both are false. All we need is the equation we have
already used
E/c = pL
which says that the momentum of a photon is
expressed by E/c. This equation comes from previous theory and
has nothing to do with relativity. If we assume that light can
have a mass equivalence, then we have
E/c = m0v
E
= m0c2
where m0 is the mass equivalence of the light. MM's
photon has a mass equivalence of m0 in this particular
problem. Putting this into MM's equation above yields
K =
-F0(v'/c)
αF0 = F1
K
= -m0c2(v'/αc)
But we want kinetic energy in terms of m' not m0.
m0
= m'v'/c
K = -(m'v'/2c )c2(v'/αc)
K =
-(1/α) m'v'2/2
To put in some
hypothethical numbers: If vav' =.2c, then v' =.4c, and
K = .714 x 5.55 x 10-36kg x (1.2 x 108m/s)2/2
= -2.85 x 10-20J
Now let us calculate
equations from the zero-point
K = (1 - α)F0
{For α we will
use 1/[1 - (v/c)] instead of 1 + (v'/c)]}
K = -(v/c)m0c2
m0
= (m - m')/2
mr = m' - m0
m0
= [m - (mr + m0)]/2
3m0 = m -
mr
K = -(m - mr)(v/3c)c2
-3cK/v = mc2 - mrc2
-K ≠
mc2 - mrc2
Which means that if
ET = K + mrc2
ET ≠ mc2
ET = mrc2
- (v/c)m0c2
= mc2/β -
(v/2c)c2 [m - (m/α)]
= mc2/β
- (v/2c)[mc2 - (mc2/α)]
=
mc2[(1/β) - (v/2c) + (v/2αc)]
ET
= mc2[1 - (3v/2c) - (v2/2c2)]
=
3.70 x 10-19J
Now let us find ET in
terms of mr, so that we can compare the transform to
gamma.
ET = mrc2 -
(v/c)m0c2
mr = m' - m0
m0
= mrβ/α - mr
ET =
mrc2 - {mr(v/c)c2[(β/α)
- 1}
= mrc2
- {mr(v/c)c2[v/(2c - 3v)
ET = mrc2{1
- [v2/(2c2 - 3cv)]}
K = {mrc2{1
- [v2/(2c2 - 3cv)]} - mrc2
Having checked this against MM's previous numbers and one finds that indeed
this also is
-2.85 x 10-20J
MM calls this
transformation term kappa2, κ2.
κ2
= 1 - [v2/(2c2- 3cv)]
Notice that it is
not the equivalent of either gamma or beta
(although it is very close in output to gamma).
@ v =
.286c, κ2 = {1 - [v2/(2c2
- 3cv)]} = .929
If we
had been in an experimental situation where the kinetic energy
had been positive, then we would have found the inverse of this
number using kappa1, which is
κ1
= 1 + [v2/(2c2 - 3cv)]
= 1.07
To
show you how close we are to current experimental values, if we
had used the average velocity in this equation, we would have
found
kappa1 to be 1.01
gamma (@
v = .143c) = 1.01
An exact match. Astonishing, considering
all the mathematical and conceptual changes MM made in Einstein's
derivations. But he was not able to derive the classical equation
from his thought problem, and MM can:
-3cK/v = mc2 -
mrc2 (from above)
mc2 - m[1 -
(3v/2c)]c2 = -3cK/v
multiply both sides by
v2/c2
mv2 - m[1 - (3v/2c)]v2
= -3Kv/c
(3v/2c)]mv2 = -3Kv/c
K = - mv2/2
= -2.85 x 10-20J
Absolutely incredible! Once Einstein's variable
assignments are corrected it turns out that the classical
equation is precisely correct. Einstein and current wisdom both
treat the classical equation as an approximation at slow speeds
relative to c. As supposed proof of this, they expand the square
root in gamma using the binomial expansion, the first
uncancelled term being v2/2c2. But this is
once again a fortuitous collision of luck and bad math. MM has
shown that gamma is an incorrect transformation term, so
that expanding the square root of the term is pointless. If there
is no gamma, there can be no expansion of the square root and no
proof of the approximation of mv2/2. Besides, this
expansion proposes to find that
K ≈ mrv2/2
Which is absurd. What should have been intended is to show that K ≈ mv2/2 at slow speeds
This
latter equation is the classical expression of kinetic energy. As
MM has shown, expressing kinetic energy in terms of a rest mass
isn't even sensible, once it is understood what the different
terms mean. The relativistic equation would have to resolve to
either mv2/2 or m'v'2/2 at slow speeds,
even if gamma and Einstein's theory and the binomial
expansion were all completely correct. Having it resolve to
mrv2/2 is just further proof that no one
knew what was going on with the math and the variable
assignments. You cannot have a rest mass in a kinetic energy
equation because a mass at rest has no kinetic energy. Or, to be
more precise, you cannot express mass as rest mass in your
central and fundamental kinetic energy equation. K = mv2/2
is not some lead-up equation. It is the basic expression (and
definition) of kinetic energy. It is therefore illogical to use a
rest mass as your variable.
Clearly up some
rough spots, MM has used Einstein's thought problem to find his
energy equations, after a good bit of scouring. But in his
thought problem the transform is done on the frequency of the
light. This makes sense except for one thing: MM explicitly said
in his own thought problem that the ball does not use E' in its
equations on the photon. How can the two statements be reconciled?
In the momentum
equation m'v' = E/c, it is stated that the ball does not use E'. And
this is true. In this equation, the equality applies to two
numbers that are both generated by the same field, that field
being the field of the zero-point. m'v' is relative to the
zero-point, therefore E/c must also be relative to the
zero-point. E'/c is not relative to the zero-point; it is
relative to the coordinate system of the ball.
But in Einstein's thought problem, we are not
creating a momentum equality, or conserving momentum. We are
transforming from one system to another, A to B. We are
transforming the energy of the light from E to E' at the same
time that we are transforming masses and total energies. We must
therefore include in the derivation E', which is the energy of
the light measured from the ball. E' is a necessary variable in
his problem. In MM's initial thought problem it is not.
The
second rough spot concerns the variable v'. In MM's mass transform
equations, vav was the average velocity. But in using
Einstein's thought problem, MM shows that v must be the final
velocity of the body. Some may ask why MM did not simply let v be
the final velocity in MM's own thought problem. It was foresight
that made MM do it (and the Work-Energy Theorem). Remember that
the ball, when it is calculating its own velocity, is in
possession of only two pieces of data. It has an elapsed time and
a distance. It also knows it started from rest. It therefore must
assume an acceleration over one part of the distance or all of
it. According to the Work-Energy Theorem, the ball may not assume
that a final velocity was achieved instantaneously or over no
distance. There is a kinetic energy because there is work (and
vice versa) and there is work because there is time and distance
involved. A force cannot be exerted over zero time or distance.
Since MM knew that kinetic energy would be both the end product
and the driving "force" of MM's thought problem, MM was
astute enough to let v be what it must be under the situation—an
average velocity. Of course this gives us just one more thing to
be very careful about. Each problem has its own specific variable
assignments, which have to be written out in full and kept track
of. Even α does not always contain the same variables. In
MM's mass transforms, the velocity variables in α are average
velocities. In MM's time, distance and velocity transforms it does
not matter, since no acceleration is involved. In the light
frequency or light energy transforms, the velocity variables are
commonly assumed to be final velocities.
The last rough
spot concerns the use of both v and vav in the
derivation of the energy equations.
When transforming the
masses within the energy equations, MM am using α with vav.
But the final equation is expressed in terms of v. Isn't this an
illegal mathematical substitution? No. It is perfectly legal to
use v and vav in the same equations, as long as you
keep track of them. As you can see, α has the same value
whether you use v or vav, as long as you use the
correct form of alpha each time. Therefore canceling
alphas from one equation to the next is not a problem.
The
equations and terms we found above apply only to the thought
problem with the ball. MM has shown, both in this paper and in MM's
paper on the time and velocity transforms, that there is no one
problem in Special Relativity. Trajectories must always be taken
into account. Which means that if we want to generalize the mass
and energy transforms we must do a bit more work. We must be sure
that what seems to be true, is true. In other words, we must run
the equations for 1) Einstein's problem with the light planes—in
which there is a mass change but no velocity change—and
also for 2) A problem in which the relative velocity is toward an
observer. Only then will we fully understand the mechanics of
mass and energy in Relativity.
So let us return to
Einstein's thought problem. His problem is different than MM's ball
problem in that he has both a final and an initial kinetic
energy. MM's ball started at rest, so that its initial kinetic
energy was zero. These should have been Einstein's final
equations, according to MM's corrections:
L = 2F0
ΔK
= L[1 - (1/α)]
ΔK = L(v/c)
Whereas MM's final
equations for the ball were:
ΔK = (1 - α)F0
ΔK = -F1(v/c)
So let us find the
equations for Einstein's problem
ΔK = 2F0(v/c)
In
his problem, the body measured the normal frequency for the
light, so that F0 = m0c2
ΔK
= 2m0c2(v/c)
But we want kinetic energy in terms of m not m0.
2m0
= mv/2c (MM used the equation m0
= mvav/c from above; but we must use the total mass of
the light planes, which is 2m0.)
ΔK =
2(mv/2c)c2(v/c)
ΔK = mv2/2
ET
= mrc2 + 2(v/c)m0c2
mr
= m' - 2m0
2m0 = mrβ/α
- mr
ET = mrc2 +
{mr(v/c)c2[(β/α) - 1}
ET
= mrc2{1 + [v2/(2c2–
3cv)]}
K = {mrc2{1 + [v2/(2c2–
3cv)]} – mrc2
ET =
mrc2 + 2(v/c)m0c2
ET
= (1/β)mc2 + (v/c)[(m/α) - m/β)]c2
ET
= mc2 [(1/β) + (v/αc) - (v/cβ)]
ET
= mc2 [1 – (3v/2c) + (v2/2c2)]
We have proven that the classical equation also applies
to Einstein's thought problem, and that ET ≠
mc2 there either.
But we are finally in a position to show that Einstein chose his
thought problem carefully. He wanted avoid an acceleration and
the use of average velocity that MM's problem entailed. So he chose
a problem with no velocity change at all. Kinetic energy changes
only because the mass has changed. But this has the effect of
oversimplifying the problem of energy transformation due to
Relativity. Notice that it is difficult to understand where to
apply the Work-Energy Theorem in Einstein's problem, since
it is unclear where there is any force. You can't have a
force without an acceleration, and there is no acceleration here.
What has happened is that the two forces from the two light
planes have cancelled each other out. You have forces, but they
have added to zero. Some may say that is the beauty of the
problem. It sidesteps all non-critical issues. But by
sidestepping them it has cloaked them, historically. Einstein's
problem was too subtle by half. It was so subtle that it confused
Einstein himself. What is more, by generalizing his findings from
this one very unique thought problem (which was not at all
general—it was not a standard problem of mass increase or
energy transformation) he hid all the variations of mass and
energy in Relativity. MM's thought problem is both more standard
and more complex, so that it shows all the issues involved in
solving problems of this nature.
Now, what if we have a
thought problem where the velocity is toward an observer? The
kinetic energy will be positive, but the masses will show a
decrease. Let us return to our ball and our photon. We will
imagine two white lines drawn on the ground now, instead of one.
The ball starts at the first white line, as before, but this time
it is propelled toward the second white line, where we put an
observer. Everything else is the same as in the first experiment.
The momentum equalities will be the same, except that alpha
for both the velocities and the masses will be inverted. Alpha
in this problem will take the value α2 = 1 –
(v'/c) = 1/[1 + (v/c)]
Alpha in the energy transform of the photon must stay in the
original form, however, since the ball will still be measuring a
redshift. The observer will be measuring a normal frequency, just
as in the first problem. We must be very careful here, since we
have two values for alpha. Not just two equal
constructions, as in the first problem; now we actually have
different values. We will call the original alpha α1,
and the new alpha α2.
E1 =
E0 - F0
H1 = H0 -
F1 [Some will want to add F1
to H0 here, since we have changed directions. But if
we subtract the photon's energy in one system, we must do
so in the other system as well. The body cannot lose the mass
equivalence of the photon in one system and gain it in the
other.]
K = H1 – E1
F1
= α1F0
K = H0 - α1F0
-(H0 - F0)
= (1 - α1)F0
= -(v/c)F1 = -(v/c)m0c2
K
= -mv2/2
What
happened? We still got a negative kinetic energy. Everything
worked out just like our first problem. But we know that the body
must have a positive kinetic energy relative to the observer,
since it is now moving toward it (it was at rest to start, of
course). The reason we got a negative value at the end is that
the equations don't know the difference between one white line in
our system and the other. The equations only know the difference
between one system and another. This series of equations gives us
values relative to the zero-point of the experiment, which has
not changed. We moved our observer, but we did not change the
point of emission. The equation does not recognize that our
observer has moved, since we did not add any pertinent
information to the equation. The movement of the observer took
place only in our heads, not in our math. The point of emission
is behind the ball, therefore the kinetic energy, as a vector, is
still negative. In order to get the right direction, we must make
the change by hand. Anyone who has done a lot of vector equations
knows that this kind of thing is a common feature of directional
problems. The equations don't always yield the desired
information, since it is often impossible to include the
pertinent postulates into the math. That is why it is so critical
to be able to visualize vector problems and other geometric
problems. Juggling equations is not sufficient. No problem in
history has made this clearer than Special Relativity.
K =
mv2/2
ET = mrc2 + (v/c)m0c2
mr = m' - m0
m0 =
mrβ2/α2 - mr
ET
= mrc2 + {mr(v/c)c2[(β2/α2)
– 1}
β2 = 1/[1 + (v/2c)]
ET
= mrc2{1 + [v2/(2c2+
cv)]}
K = {mrc2{1 + [v2/(2c2+
cv)]} – mrc2
ET = mrc2
+ (v/c)m0c2
ET = (1/β2)mc2
+ (v/c)[(m/α2) - m/β2)]c2
ET
= mc2[1 + (v/2c) + (v2/2c2)]
We have now found three different transforms for three different problems. The only thing that has remained constant is that K = ±mv2/2
which can be considered ironic in that this was the one equation
that was thought to be an approximation; also the one equation
that was thought to have been superceded. One very important
thing is different from classical theory, though, and that is
that MM has shown that v has a limit at .5c. Using gamma,
physicists now think that v (the velocity as measured from a
distance) can approach very close to c—since this is the
value for v that gamma gives them. MM has shown that
v'—which is the true velocity of the body—may
approach c; but v may not. This is not a great difference in
theory—in that currently the variable v is thought to be
the real velocity of the object. But it does take some getting
used to, experimentally. An experimental physicist must now use
either one of the equations
K = mv2/2
or
K = {mrc2{1 + [v2/(2c2–
3cv)]} – mrc2
since in an experimental situation he or she will
always be dealing with mass as measured from a distance. That is
to say, m' is the mass as measured by the proton or
electron itself, for instance, so it will not be part of our
data. Therefore v' cannot be calculated directly, by using
one of the primed equations. The scientist will first discover v
and then calculate v' from that.
Part Eight - The Accelerator Problem - (Why 108?)
The
one variation of this problem we have not solved is the one that
will prove this theory of MM's beyond any doubt. That variation
is the real problem of subatomic particles that achieve high
velocities in accelerators. Notice that this problem is not like
any of those we have solved. We have found transforms when 1) a
body with an initial velocity emits a smaller body, but does not
change velocity, 2) a body initially at rest emits a smaller body
and moves away from an observer, and 3) a body initially at rest
emits a smaller body and moves toward an observer. We now seek
the situation when 4) a body with an initial velocity is
bombarded by smaller bodies and achieves a final velocity. This
case is obviously closer to Einstein's slowly accelerated
electron, except that in this case the subatomic particles are
not slowly accelerated.
Thought
Experiment 4:
Let us reverse the situation of our 3rd thought experiment—where
a body at rest emitted a photon—and ask what would happen
if the body instead absorbed a photon. Let us call our body a
proton, so that we can assign it a known rest mass (mr
=1.67 x 10-27kg).
Now, we discovered an equation for mass increase with the
emission problem, but this equation implies that we cannot
increase the mass by more than 4 times, even if we take the
proton all the way to c. m = mr/[1
- (3v/2c)]
Remember that v cannot exceed c/2. In MM's math it is the variable v' that has a limit at c. However, we know from experiments in particle accelerators that the mass of the proton hits a limit at 108mr. We imagine this means that the proton in the accelerator is accelerating by absorbing energy from the acceleration field. To see what MM means by this, notice that both MM's emission problem and Einstein's various thought problems all imply that when a body emits a photon, it not only gains an acceleration from the emission, it also loses mass or mass equivalence by losing the “body” of the photon. In other words, the photon leaves a hole. The rest mass of the body decreases after the emission. That is what Einstein's variable assignments tell us (E1 = E0 - F0). This would be expected, since a body can hardly emit a smaller body, no matter whether that body is a particle of light or not, and expect to keep the same amount of rest energy.
This means that if we reverse the process, the body must gain an acceleration and gain rest mass from the absorbed photon. It gains a sort of double energy increase. Let us use our math from previous papers to express this.
In a real accelerator, the proton is taken to speed in a series
of accelerations. This is an experimental concern, however, not a
mathematical concern. Scientists do not use one super-field to
accelerate since they 1) cannot create it, 2) cannot keep it from
destroying the proton if they did create it. But we can simplify
the math by allowing ourselves to imagine a super-high frequency
photon with which we will bombard our proton in a single go. The
proton will absorb this giant photon and we will see if the math
we achieve from this absorption can explain the number 108. If it
can, then we will have taken a decisive step in proving these
corrections to Special Relativity. No one has yet been able to
derive this number, and there is currently no theory to explain
why there is a limit. The accepted term gamma
implies an infinite mass increase capability; nor has the math of
quantum theory predicted the existence of a limit or the number
108.
First we must differentiate between our different
masses and mass-equivalences.
m0
= mass equivalence of the photon
mri
= rest mass of proton before absorption = 1.67 x 10-27kg
mrf
= rest mass of proton after absorption, measured from B
m =
moving mass of proton, measured by an observer
m' =
moving mass of proton, measured by the proton, relative to the
observer
By the conservation of momentum, the momentum of
the proton+photon after the absorption must equal the momentum of
the photon before.
mv/2 = E/c [remember that we must use the
average velocity]
E = m0c2
m
= 2m0c/v
m0
= mv/2c
1/α =1 – (v/c)
v/c = 1 –
(1/α)
mv/c = m – m'
m0
= (m – m') /2
mrf
= mri
+ m0
m'
= mri
+ 2m0
m'
= mrf
- m0
+ 2m0
= mrf
+ m0
m/α
= mrf
+ m0
= mrf
+ mv/2c mrf
= m[1 – (3v/2c)]
Still the term beta.
But let us find m in terms of mri
and mri
in terms of m0.
m/α
= mri
+ mv/c
mri
= m[1 – (2v/c)]
m0
= mv/2c
mri
= 2m0[(c/v)
– 2]
So we only need to return to Einstein's
equations to make the proper corrections.
E0 = the initial energy of the proton before absorption of the photon (A as background).
E1 = the total energy of the proton after the absorption of the photon (A)
H0 = the initial total energy of the proton as seen from the zero-point (B)
H1 = the final total energy of the proton as seen from the zero-point (B)
F0 = the energy of the photon in A
F1
= the energy of the photon in B
F1
= F0α
since F1
> F0
E1
= E0
+ F0
H1
= H0
+ F1
E0
= H0
since the proton is initially at rest in both systems, A and B
H1
– H0
= F1
= αF0
And
the final kinetic energy is represented by
K = H1
– E1
=
H1
– (E0
+ F0)
= H1
– (H0
+ F0)
= αF0
- F0
= (α - 1)F0
= (v/c)F1
K
= (v/c)m0c2
m0
= (m – m')/2
mri
= m' - 2m0
m0
= [m – (mri
+ 2m0)]/2
4m0
= m – mri
K
= (m – mri)(v/4c)c2
4cK/v
= mc2
– mric2
K ≠ mc2
– mriic2
4cK/v = mc2
– mric2
mc2
– m[1 – (2v/c)]c2
= 4cK/v
multiply both sides by v2/c2
mv2
– m[1 – (2v/c)]v2
= 4Kv/c
(2v/c)]mv2
= 4Kv/c
K = mv2/2
Which means that if
ET
= K + mrfc2
mrf
= mri
+ m0
ET
= K + mric2
+ m0c2
ET
= mric2[1
+ (v'/2c)]
[1 – (v'2/c2)]
ET
= mric2{1
+ [(v2
+ cv)/(2c2–
4cv)]}
ET
= mc2
[1 – (3v/2c) + (v2/2c2)]
ET
= mc2
[1 +
(v'/2c)]
[1 + (2v'/c) + (v'2/c2)]
Notice
the last bolded equation above tells us why gamma
works so well in accelerators despite being slightly incorrect
and being derived with so many mistakes.
In accelerators
we are finding a limit at 108. Therefore, we set MM's equation
equal to 108 and see what velocity the proton is really
achieving.
(v/c)m0c2
+ m0c2
+ mric2
= 108mric2
(v/c)m0c2
+ m0c2
= 107mric2
This last step was allowed since mri
is the same in both theories.
[(v/c) + 1]m0
= 107mri
mri
= 2m0[(c/v)
– 2]
[(v/c) + 1]/[(c/v) - 2] = 214
v = .4982558c
v'
= .9930474c = 2.97708 x 108m/s
c
= 2.99792458 x 108m/s
According
to current theory, gamma
is equal to 108 at v = .999957c. The v variable in gamma
is equivalent to MM's v', since current theory has no v',
and since MM has defined MM's v' as the true velocity of the
object.
So, we now have all our numbers in hand. How am MM
going to explain the number 108? Notice that we have an
unexplained velocity differential in both current theory and MM's
theory. By current theory the limit in velocity for the proton is
1.2 x 104m/s
less than c. By MM's theory the gap is a bit larger: 2.1 x 106m/s.
What causes this gap? And which gap is correct? If one can answer
these questions, then one can show where the number 108 comes
from.
Let's say that the proton already has a velocity or velocity equivalent due to some motion or force or other unexplained phenomenon. Let's say that the proton's total velocity cannot exceed c, and that this other unexplained motion or force makes up the difference. That is precisely what Miles Mathis has done in G is the Key to the Secret of Gravity.
Using a hint
of Maxwell and the dimensions of G, MM showed that the proton can
be shown to have a constant acceleration in any direction of 8.88
x 10-12m/s2.
Here is a gloss of that math. Given two equal spheres of
radius r touching at a point, we have
F = Gmm/(2r)2
ma
= 2Gmm/(2r)2
a = 2Gm/4r2
a/2 = 2Δr/2Δt2
We now let the spheres expand at a constant and equal rate.
We assign Δr to a change in the radius instead of a change
in the distance between the spheres, and this allows us to
calculate even when the spheres are touching.
Δr/Δt2
= Gm/r2
After
time Δt, the radius will be r + Δr. After any
appreciable amount of time, r will be negligible in relation to
Δr, so that Δr ≈ r + Δr
m = Δr3/GΔt2
a
= 2Δr/Δt2
a
= 2mG/Δr2
That
is the acceleration of each of two equal masses in a
gravitational situation. But if we want to give all the
acceleration to one of them, holding the other one steady for
experimental purposes, then we simply double the value.
a =
4mG/Δr2
If the proton has a radius of 10-13m,
this yields
a = 8.88 x 10-12m/s2
If we allow the proton to accelerate at this pace over its entire lifetime up until the current moment, then we can achieve a number for its present velocity due to mass. MM's velocity is a much better fit.
Using this acceleration due to mass and gamma,
we get an age of the proton of only 85 million years.
v = at/2
= 2
x 1.2 x 104m/s
= 85 million years
8.88 x
10-12m/s2
MM's corrected numbers give an age of the proton of about 15
billion years.
v = at/2 = (8.88 x 10-12m/s2
)(4.73 x 1017s)/2
= 2.1 x 106m/s
MM's number is therefore a match to current estimates, as you see.
Current theory based on gamma
is clearly wrong, since the proton cannot be as young as 85
million years. That would make protons 50x younger than the
earth.
[To see a shorter way to derive the number 108, see Redefining
the Photon. There, MM uses the density of the charge field to
calculate the number.]
Conclusion
MM's mathematical connection of this paper with MM's other papers on mass and gravity does several very important things.
|
All these concepts are not separate ideas, they are different expressions of the same thing. And they all resolve to length over time. These last claims were not proved in MM's paper An Algebraic Correction to Special Relativity, much less here, but they are proved in links to other papers, and MM's mass increase paper is one of the central pillars in that proof.
footnote 1
Miles Mathis has been asked where the 2 comes from when he writes e 2v'av/c
in the denominator of MM's velocity transform above. In answer,
consider that the fraction v/c is the real transform here, so we
have to be careful to get it right. We are comparing v to
c. So we can't compare v'av
to c. If we did that, we would be implying that the object
accelerated to speed over some interval while the light did not.
But since we assume light is material just like our object,
we cannot imply that. The light may accelerate to speed
extremely fast, but it still must accelerate. Since our
given number for c is obviously a final velocity, we must also
use a final velocity for our object.
You will say that we have no indication light accelerates to speed when emitted, but that empirical fact is beside the point in this particular thought problem. Since we are ultimately calculating momenta and energies from this thought problem, we have to let the photon accelerate at emission, otherwise it wouldn't be capable of creating a force back on the object. If we let light be emitted with no acceleration, it couldn't create an equal and opposite force back on the object, you see. It would just slip out of the object with a whisper, and no force back would be created. So to compare v to c and obtain any sort of momentum—using the conservation of momentum—we have to assume light accelerates at emission. If we assume that, then we have to use a v final in that position to make the equations work.
A line-by-line critique of Einstein's paper on Special Relativity in Annlen de Physik 17 1905 titled:
"On the Electrodynamics of Moving Bodies"
§3. Theory of transformation of coordinates and time from a system at rest to a system in uniform translational motion relative to it
Here Miles Mathis will critique Einstein's original paper of 1905—probably the most famous physics paper of all time (in 1944 a manuscript was purchased for $6 million—who knows what it would fetch now). MM has copied the 2 and 1/2 pages of equations that lead up to gamma here, so that you can follow along, line for line.



The first part of the article is just an introduction to the problem, which MM will not repeat here. It is perhaps better to approach the problem fresh, anyway. It is much simpler than history has made it.
In short, Einstein has one important postulate to add to Newton and Galileo. It is this:
"Any ray of light moves in the stationary system of co-ordinates with the determined velocity c, whether the ray be admitted by a stationary or moving body."
This is just a restatement of the constancy of c, but it is a precise wording of it, and it will come up very soon in his math. That is why MM quotes it in full. It is the second of two "basic principles" of relativity. The first principle is that systems or bodies in "uniform translatory motion" relative to each other have the same laws. That is, neither one is primary: either may be taken as "at rest." This is not so much a postulate as it is an hypothesis (as Einstein admits in this paper) but since MM agrees with the intent of both principles, it does not matter here.
MM will touch on one point before moving on. Principle 2, quoted above, already contains a confusion of terms. A moving body requires a second co-ordinate system—that is why Einstein invents multiple systems to begin with: to explain the motion. But the second part of principle 2 ignores this fact. He says, "whether the ray be admitted by a stationary or moving body." But, obviously, if the ray is admitted by a moving body, it is not in "the stationary system of co-ordinates." It is in the moving system of co-ordinates. A better statement of principle 2 would have been that light is measured to travel c, from any and all co-ordinate systems.
Very soon after this Einstein introduces his two co-ordinate systems, which in this paper he calls K and k, where K is the stationary system. Then he gives us the variables, x, y, z, and t in K; and ξ, η, ζ and τ in k. In short, given x and t, he wants to find a transformation term that will express ξ and τ [ ξ and τ were replaced by x' and t' in later algebraic derivations, such as the one in his book Relativity].
The last thing we are given is a velocity v. This, Einstein tells us, is the velocity of the entire system k in "the direction of the increasing x of K" But, MM asks, is this the velocity of k as measured from k, or as measured from K? Einstein does not tell us, though it is absolutely crucial that we know. K and k each have their own clocks and measuring rods, which are not equivalent (by the rules of Relativity). They will therefore each measure velocity differently. In fact, they will measure the velocity of k differently. But Einstein does not assign v to either system. This is Einstein's greatest error in the whole derivation of gamma. Since v is unprimed and un-Greek, you may assume it is k as measured from K. But if this is true, then the velocity of k as measured by k must have a value too. Notice that Einstein never once, in this or any other derivation, creates a variable for that v, nor does he discover an equation which yields it. [The velocity we get in later equations—the velocity of the current v tranformation—is the velocity of an object moving within k. It is not the velocity of k itself.]
Then we get the equation x' = x - vt. Einstein says,
"If we place x' = x - vt, it is clear that a point at rest in the system k must have a system of values x', y, z independent of time. We first define τ as a function of x', y, z and t. To do this we have to express in equations that τ is nothing else than the summary of the data of clocks at rest in system k, which have been synchronized. . ."
So, he states outright that x', y, and z are now the set of variables "at rest in the system k." But he has already assigned y and z to K. A point at rest relative to k is moving relative to K, since k is moving relative to K. So "at rest in the system k" is not equivalent to "at rest in K". This being true, it also means that ξ, η, and ζ have just been bumped up into a third system—the system that is moving in k—which he has no label for. But x' is a variable with two allegiances: he says it is now in k, but by the equation x' = x - vt it is still connected to K. Unless he means for x and v to also be "at rest in k", in which case we might as well do away with K altogether—it has become superfluous. Likewise, the variable t is also a dual citizen. Einstein has it variously in K and k. When it is with x', it is in k. When it is with x, it is in K. Tau (τ) is in the undefined third co-ordinate system, with ξ, η, and ζ. Notice especially that Einstein has created an x' but no t'. He has three x variables but not three t variables.
He then says, "From the origin of system k let a ray be emitted at the time τ0 along the x-axis to x', and at the time τ1 be reflected thence to the origin of the co-ordinates, arriving there at the time τ2."
So the ray takes the place of the man in the train. Einstein has a movement within a movement here: k is moving in K, and the light ray is moving in k. This provides two degrees of relativity, which Einstein is trying to calculate at once. But he does not seem to realize that he is doing this. He doesn't have enough variables to do it successfully, so his variables keep sliding from K to k. He needs three sets of variables and three co-ordinate systems.
The other mistake is to use a light ray for his object moving in k. Principle 2 states that light is measured c, whether from a moving or stationary system. This makes light a special case. It is not like a man on a train. c, unlike v or v', does not change with position of measurement. This is Einstein's second greatest error in this paper.
Next he prepares for a bit of calculus—that is why he is talking of functions. He doesn't need calculus here, but it is the only way he can get the reader more confused. He gives us this strange equation:
1/2[τ(0,0,0,t) + τ(0,0,0, t + x'/(c - v) + x'/(c + v))] = τ(x', 0,0, t + x'/(c - v))
This is a preparatory step to differentiation, but we don't need to go there since this equation is faulty. It is supposed to be an expansion of
1/2(τ0 + τ2) = τ1
But the corresponding time at τ1 in either k or K is not t + x'/(c - v) . First of all, this violates Einstein's own Principle 2, which was quoted in full above. The speed of light must be measured the same from anywhere. But Einstein himself is subtracting v from it!
Before giving us a partial equation for τ, supposedly from all his differentiation, he tells us that "light is always propagated along these axes [Y and Z], when viewed from the stationary system, with the velocity √(c2 - v2)." All that, as an aside, almost as a footnote. He gives us no equations to show why light should move like that along the Y and Z axes. Where did that square root come from? One can only suppose he borrowed it from somewhere, most likely Lorentz. But it just stands there, naked, with nothing leading into it and nothing leading out. Obviously it is supposed to be the old Pythagorean way of comparing the two light rays in the interferometer, that MM has already critiqued. But we don't have two light rays here. He has given us one light ray going up and back, in the x-direction of both K and k. So his equation for Y and Z is false—he has given us v as the velocity in the x-direction. We have no velocity in the Y or Z direction, not in K or k.
What is more astonishing is the fact that he again violates Principle 2. He says, "when viewed from the stationary system." But Principle 2 reads, "Any ray of light moves in the stationary system of co-ordinates with the determined velocity c, whether the ray be admitted by a stationary or moving body." k is that moving body.
Finally, Einstein gives us this equation:
τ = a[t - vx'/(c2 - v2)] where "a is a function of v at present unknown."
Then he gives us this
ξ = cτ
This is the equation that becomes x' = ct' in the book Relativity. MM has already shown that it is false [in several other papers], since time dilating implies a larger τ, not a smaller. But by substituting this false equation into the previous one we get,
ξ = ac[t - vx'/(c2 - v2)]
Then Einstein says that t = x'/(c - v), which MM has just shown is wrong. But he substitutes it into the above equation.
After simplifying he gets,
ξ = ac2x'/(c2 - v2)
then he substitutes x - vt for x', which yields,
ξ = ac2(x - vt)/(c2 - v2)
Then, as you can see, Einstein gives us some more nonsensical equations for η and ζ. Being in the y and z directions, they can have nothing to do with v, which Einstein told us at the top of p. 43 was "in the direction of the increasing x of K."
But we are basically finished. c2/(c2 - v2) is our transformation term. Einstein calls it β here, but it has come to be known as γ. He never had a β variable in any equation, but it suddenly appears at the end as the thing we were looking for all along. The variable "a" has been lost to the dustbin in all the rewritings of these equations, with no explanation that MM has ever seen.
Einstein's final error is a simple mathematical one. He assumes that
c2/(c2 - v2) = 1/√(1 - v 2 /c2)
When in fact it is simply
1/(1 - v2/c2) —There is no square root.
Either he reduced the equation wrong, or he has some hidden math steps here he is not sharing with us. It may be that he thinks that those last y and z equations will affect his transformation term β somehow. But in his rewriting of the math in later books, he does not assume that y and z affect calculations in the x-direction. Nor does anyone who parrots this derivation of gamma. But if you think about it, the only way to get a Pythagorean square root into a linear problem in one direction, is to mess it up in just this way—to assume, for some reason, that an x-velocity is affected by y and z.
One final point. Einstein later changes the math of Special Relativity. It has been said that he did this to simplify it for general audiences, specifically for the book Relativity. Those who say this also point to the fact that he changed the math to make it even more difficult after he completed General Relativity. For, at that time, he imported the tensor calculus used in General Relativity to express Special Relativity. In his lectures at Princeton he used this very difficult math. He had two derivations of Special Relativity working after 1916: one a revamped algebraic derivation (in the appendix of Relativity) that is very similar to the one MM showed in this paper, the other a tensor calculus derivation.
But both changes mask the basic errors of the original paper—they do not fix them. In the algebraic solution, he gets rid of the Greek letters. Unfortunately he replaces ξ with x'. But they are far from equivalent. x' is the x-variable in a non-moving k, as he states above. ξ is the x-variable moving within k. It is the x-variable that belongs to the light ray, which is moving. Nor does he fix the equation x' = ct'. It is false whether the x-variable is ξ or x'.
The tensor calculus derivation also takes all the givens of the paper of 1905 as still given. It fixes none of them. All it does is make the contradictions harder to see. There is absolutely no reason to use tensor calculus to solve the problem of Special Relativity, as Einstein presents it and as it stands to this day. It does not even call for regular calculus, as Einstein proved in the appendix of his book. A problem should be solved with the simplest math that will solve it—especially a problem of applied math. This keeps the concepts and assumptions as near to the surface as possible, where they may ride out the light of day.
Now let us look at Einstein's derivation of the equation for the addition of velocities. In his 1905 paper he did not differentiate his x equation in order to find his relative velocity equation, like they do now in textbooks. He simply combined his equations algebraically, like this:
From earlier in the paper Einstein found:
γ = gamma = 1 /√(1 - v2/c2)
τ = γ(t - vx/c2)
ξ = γ(x - vt)
Now he says, if a point is moving in k,
let ξ = wτ where w "is a constant".
Notice two things. One, Einstein now has a point moving in k instead of a light ray. He seems to have recognized his earlier mistake, and he changes his moving object from a light ray to a point. This is really odd. If MM is right and he noticed the theoretical difference between the light ray and the point, then why didn't he go back and correct the first part of the derivation. On the other hand, if MM is wrong and he didn't see his mistake, why did he make the basic change? You don't normally change your objects in the middle of a derivation.
Two, he does not define this new velocity variable at all, beyond saying it is a constant. This is really extraordinary. One must look at the sentences two or three times, to be sure that he intends w to be the velocity variable. He does not fully define w, because he can't. If he states outright that it is a velocity variable, then he must assign it to one of his co-ordinate systems. Very soon you will see why that would be fatal to him.
By substitution, he gets,
wτ = γ(x - vt)
wγ(t - vx/c2) = γ(x - vt)
wt - wvx/c2 = x - vt
x + wvx/c2 = wt + vt
x(1 + wv/c2) = (w + v)t
x = ( w + v )t
1 + wv/c2
Now, watch this last step very closely. He reduces the above equation to:
V = w + v
1 + wv/c2
This is the current value for V. This equation stands to this day.
But to reduce like he did he must assume that V = x/t
We have been given that w = ξ/τ
So what does v equal? v is what x over what t?
V = x/t
w = ξ/τ
v = ?/?
You may say, well maybe the x is x'. Maybe, but what is the t? He has no third t-variable anywhere, in this paper. And in later derivations, when he does have a t', he has no τ. He never has three t variables.
What we need to solve for an addition of velocities, amazingly enough, is four t-variables and five x variables.
t0 = the time of K from K
t = the time of the point as seen from K
t' = the time of k as seen from K
t'' = the time of k as seen from k
τ = the time of the point as seen from k.
τ' = the time of the point as seen from the point
but t" = τ' = t0
We need five x-variables
x = displacement of the point, as measured by K
x' = displacement of k, as measured by K
x" = displacement of k as measured by k.
ξ = displacement of the point, as measured by k
ξ' = displacement of the point as measured by the point
Einstein says that v is the velocity of k relative to K.
w is the velocity of a point relative to k.
V is the velocity of that point relative to K.
but to solve we also need,
w' = velocity of the point measured by the point
v' = velocity of k as measured by k
w' = ξ'/t 0
v' = x"/t0
τ = t0 + (ξ'/c)
w = ξ'/[t0 + (ξ'/c)] = w'/(1 + w'/c)
w' = w/(1 - w/c)
v = x"/t'
t' = t0 + (x"/c)
v = x"/[t0 + (x"/c)] = v'/(1 + v'/c)
v' = v/[1 - (v/c)]
t = t0 + (ξ' + x")/c
V = (ξ' + x")/t = (ξ' + x")/[t0 + (ξ' + x")/c]
Multiply the last equation by 1/t0//1/t0
{Eq. 5} V
= v' + w'
1 + [(v' + w')/c]
V = v + w
1 - (v/c) 1 - (w/c)
v + w
1 + 1 - (v/c) 1 - (w/c)
c
= v + w - (2vw/c)
1 - v/c - w/c + vw/c2 + [v + w - (2vw/c)]/c
= v + w - (2vw/c)
1 - vw/c2
Just to be sure that gamma does not apply to the transformation of two degrees for t, let us find τ' in terms of v and t, like Einstein did.
t = t0 + (ξ' + x")/c
w' = ξ'/t0
v' = x"/t0
t = t0 + (w't0+ v't0)/c
w' = w/[1 – (w/c)] and v' = v/[1 – (v/c)]
t0 = τ'
t = τ' + wτ'/[c(1 - w/c)] + vτ'/[c(1 - v/c])
t = τ'{1 + [w/c(1 - w/c)] + v/c(1 - v/c)}
t/τ' = (c - v)(c + v) + w/(c - v) + v/(c - w)
(c - v)(c - w) (c - v)(c - w) (c - v)(c - w)
= c2 - wv = 1 - wv/c2
(c - w)(c - v) (1 - w/c)(1 - v/c)
Similar, but not gamma. Not surprising, since gamma only has one velocity variable. Notice that in Einstein's derivation of gamma, regarding x and t, he already had two velocities. His set-up for the addition of velocity section is exactly the same as his set-up for x and t, in the first section. The only difference is he had a light ray moving—as his second velocity—in the first part, and a point in the second part. But in both sections he is seeking equations for two degrees of relativity.
Now, you may say, why not use "equation 5", in the section on V above? It looks very much like Einstein's equation, except that we are adding the velocities in the denominator rather than multiplying them. At most speeds this would only be a small correction to Einstein and would seem to imply that his math was not that far off.
We can't use that equation for one very important reason. The velocity variables don't match Einstein's. Mine are prime, his were not. Mine are the local velocities of k and the point. His are actually undefined, so it is impossible to say what he meant for them to stand for. But MM assumes he intended them to be the measured velocities of the point and k, from k and K, respectively. MM assumes this because he never provides us with an equation to discover the velocity of k relative to K, or the point relative to k. He doesn't derive these equations because he thought those were his givens. But now that it turns out that his final equation suggests that his givens were local velocities, measured by the moving systems themselves. And this means that the velocity of k relative to K and the velocity of the point relative to k are still unknowns. Einstein has derived no equations for first-degree relativity!
The other reason not to use equation 5 is that in most real situations we will not be given the local velocities. In using the relativity equations on quanta, for instance, the givens are not local velocities. We would be given relative, or measured-from-a-distance, numbers to begin with, and would need an equation to determine the addition of these numbers. The famous experiment of Fizeau (explained by Einstein) is another example. We are given the speed of the liquid. But this is our determination of the speed of the liquid, not the liquid's. The given is not a local measurement of the system.
Please notice that MM's new equation for the addition of velocities gives us numbers that are very close to Einstein's in most situations. It differs from his in having another easily comprehensible term in the numerator and a minus sign instead of a plus sign in the denominator. But it may be used with confidence, since it has been derived from a thoroughly analyzed situation, as above, from five different co-ordinate systems.
The true transformation equation for velocity of one degree of relativity is the one MM used above, in MM's derivation of V.
v = v'
1 + v'/c
The results of the previous investigation: "On the Electrodynamics of Moving Bodies" lead to a very interesting conclusion, which is here to be deduced.
I based that investigation on the Maxwell-Hertz equations for empty space, together with the Maxwell expression for the electromagnetic energy of space, and in addition the principle that:—
The laws by which the states of physical systems alter are independent of the alternative, to which of two systems of coordinates, in uniform motion of parallel translation relatively to each other, these alterations of state are referred (principle of relativity).
With these principles* as a basis MM deduced inter alia the following result (§ 8):—
Let a system of plane waves of light, referred to the system of co-ordinates (x, y, z), possess the energy l; let the direction of the ray (the wave-normal) make an angle φ with the axis of x of the system. If we introduce a new system of co-ordinates (ξ, η, ς) moving in uniform parallel translation with respect to the system (x, y, z), and having its origin of co-ordinates in motion along the axis of x with the velocity v, then this quantity of light—measured in the system (ξ, η, ς)—possesses the energy
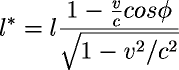
where c denotes the velocity of light. We shall make use of this result in what follows.
Let there be a stationary body in the system (x, y, z), and let its energy—referred to the system (x, y, z) be E0. Let the energy of the body relative to the system (ξ, η, ς) moving as above with the velocity v, be H0.
Let this body send out, in a direction making an angle φ with the axis of x, plane waves of light, of energy ½L measured relatively to (x, y, z), and simultaneously an equal quantity of light in the opposite direction. Meanwhile the body remains at rest with respect to the system (x, y, z). The principle of energy must apply to this process, and in fact (by the principle of relativity) with respect to both systems of co-ordinates. If we call the energy of the body after the emission of light E1 or H1 respectively, measured relatively to the system (x, y, z) or (ξ, η, ς) respectively, then by employing the relation given above we obtain
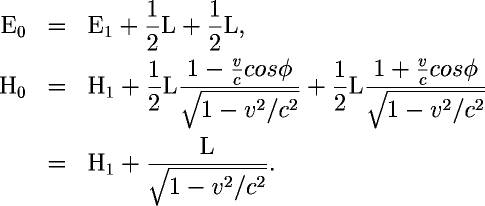
By subtraction we obtain from these equations
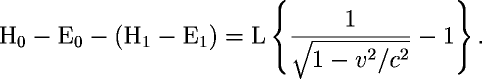
The two differences of the form H -; E occurring in this expression have simple physical significations. H and E are energy values of the same body referred to two systems of co-ordinates which are in motion relatively to each other, the body being at rest in one of the two systems (system (x, y, z)). Thus it is clear that the difference H - E can differ from the kinetic energy K of the body, with respect to the other system(ξ, η, ς), only by an additive constant C, which depends on the choice of the arbitrary additive constants of the energies H and E. Thus we may place
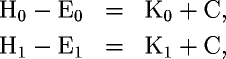
since C does not change during the emission of light. So we have
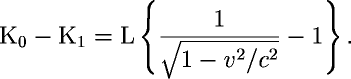
The kinetic energy of the body with respect to (ξ, η, ς) diminishes as a result of the emission of light, and the amount of diminution is independent of the properties of the body. Moreover, the difference K0 − K1, like the kinetic energy of the electron (§ 10), depends on the velocity.
Neglecting magnitudes of fourth and higher orders we may place

From this equation it directly follows that:—
If a body gives off the energy L in the form of radiation, its mass diminishes by L/c². The fact that the energy withdrawn from the body becomes energy of radiation evidently makes no difference, so that we are led to the more general conclusion that
The mass of a body is a measure of its energy-content; if the energy changes by L, the mass changes in the same sense by L/9 × 1020, the energy being measured in ergs, and the mass in grams.
It is not impossible that with bodies whose energy-content is variable to a high degree (e.g. with radium salts) the theory may be successfully put to the test.
If the theory corresponds to the facts, radiation conveys inertia between the emitting and absorbing bodies.
Footnotes
* The principle of the constancy of the velocity of light is of course contained in Maxwell's equations.