Miles Mathis: An Algebraic Correction to Special Relativity
and Refutation of Gamma
| Please note that this paper is a simplification by me of a paper or papers written and copyrighted by Miles Mathis on his site. MM has replaced "I" and "my" with "MM" to show that he is talking. All links within the papers, not yet simplified, are linked directly to the Miles Mathis site and will appear in another tab. (It will be clear which of these are Miles Mathis originals because they will be still contain "I" and "my".) The original papers on his site are the ultimate and correct source. All contributions to his papers and ordering of his books should be made on his site. (This paper incorporates Miles Mathis' simp paper, long paper, lor2 paper, and question and answer: rel222 |


Galileo Einstein
Table of Contents
-
Simplification Part One - The Current Derivation
-
Simplification Part Two - The Critique
-
Simplification Part Three - The Correction
-
Simplification Part Four - An Approaching Body, a Trajectory at an Angle
-
Simplification Part Five - The Second-Degree Transform
-
Note from Miles Mathis
-
The Primary Error
-
Abstract
-
Introduction
-
Part I: The Equation x' = x - vt
-
Part II: The Equation x = ct
-
Part III: Lorentz, Michelson and Pythagoras
-
Part IV: *New Transformation Equations Derived*
-
Thought Problem
-
Part V: Relative Velocity of an Approaching Object
-
Part VI: Relative Motion at an Angle
-
Part VII: The Addition of Velocities (two degrees of Relativity)
-
Part VIII: Conclusion
-
Part IX: Inferences (Including the Twin Paradox, Hafele Keating, etc.)
-
Part X: A Prediction (Concerning the Pioneer Anomaly)
-
Inserted Part Five Second-Degree Relativity
-
Appendix A: The Michelson Morley Interferometer
-
Appendix B: The L and t Transforms
-
Question by student
- Simplification Part One - The Current Derivation
- Simplification Part Two - The Critique
- Simplification Part Three - The Correction
- Simplification Part Four - An Approaching Body, a Trajectory at an Angle
- Simplification Part Five - The Second-Degree Transform
- Note from Miles Mathis
- The Primary Error
- Abstract
- Introduction
- Part I: The Equation x' = x - vt
- Part II: The Equation x = ct
- Part III: Lorentz, Michelson and Pythagoras
- Part IV: *New Transformation Equations Derived*
- Thought Problem
- Part V: Relative Velocity of an Approaching Object
- Part VI: Relative Motion at an Angle
- Part VII: The Addition of Velocities (two degrees of Relativity)
- Part VIII: Conclusion
- Part IX: Inferences (Including the Twin Paradox, Hafele Keating, etc.)
- Part X: A Prediction (Concerning the Pioneer Anomaly)
- Inserted Part Five Second-Degree Relativity
- Appendix A: The Michelson Morley Interferometer
- Appendix B: The L and t Transforms
- Question by student
Simplification Part One - The Current Derivation
In other papers MM has extensively critiqued the mathematical proofs of Special Relativity by Einstein, Lorentz and Minkowski. In this section the most concise explanation of the problem and its solution is presented.
Only one illustration is necessary, which the same one that will be used in the long proof later. It is the illustration of the spaceship flying by an earthbound observer—the one that MM borrowed from a textbook and modified for use in MM's longer paper.
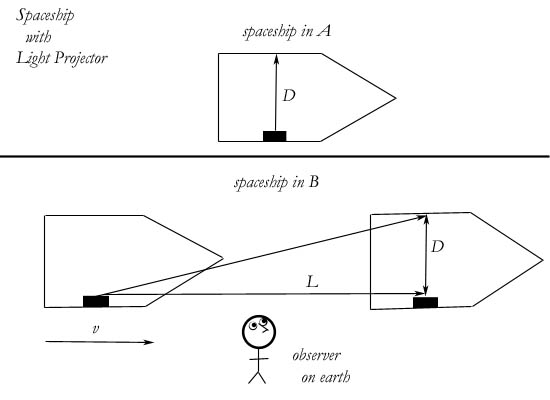
In this illustration a man walks from the near end of the spaceship to the far end. In the coordinate system of the spaceship he has walked directly away from the observer on earth, in a straight line. This straight line is x'. But from the point of view of the observer in the second coordinate system he has walked in a slant, x. This slant and the first straight line are two sides of a triangle. The third side is the distance the spaceship went from the beginning of the walk to the end. This distance may be represented by vt.
Given x' and v, we seek x.
In order to solve, we must assume several other things. These are the first assumptions of Einstein and Lorentz and Minkowski:
x = ct
x' = ct'
These equations are supposed to describe the behavior of light in the two coordinate systems. The only other assumption you need to solve is that we have created a right triangle here, allowing us to us the Pythagorean theorem
x = √x'² + (vt)²]
x = ct thus c=x/t
c = √x'² + v²t²]/t
c² = (x'² + v²t²)/t²
c² = x'²/t² + v²
c² - v² = x'²/t² [substituting x = ct as t= x/c gives] = x'²c²/x²
(c² - v²)/c² = x'²/x²
x/x' = γ = 1/√(1 - v²/c²)
And there you have it, γ, gamma, the famous transformation term. It is also the transform for the t variable. Equally simple math gives us using the bolded equation prevously:
c² = x'²/t² + v²
[substituting x'= ct']
c² = c²t'²/t² + v²
t/t' = 1/√(1 - v²/c²)
That is all there is to Special Relativity. This series of equations is equivalent to the math and assumptions of Michelson, Lorentz, Einstein, Minkowski, and everyone else in the 20th century. This simple algebra underlies the tensor calculus and has never been corrected to this day. Every explanation of Special Relativity you will find, no matter how complex, can be boiled down to this.
Simplification Part Two - The Critique
Unfortunately it is wrong in several places. The first place that it is wrong is in the light equations: x = ct and x' = ct' cannot both be true, because together they imply that x and t change in direct proportion, where in fact they change in inverse proportion. Einstein even admits this. In the book Relativity, he says (Ch.XII, p. 37) "As judged from K, the clock is moving with the velocity v; as judged from this reference body, the time which elapses between two strokes of the clock is not one second but [γ] seconds, i.e. a somewhat larger time. As a consequence, the clock goes more slowly than when at rest."
Time dilation and length contraction are now clichés. Everybody knows that time slows down and lengths get shorter. But time slowing down is a lengthening of time. When time slows down the period increases, so that the length of time between two ticks is longer. This sets up an inverse relation between x and t, and makes one of the two light equations false. It turns out that the false one is the first one, x = ct. This is simply because the x in this equation is not a length measured in its own coordinate system. x is the way a length in another coordinate system looks to an observer. x is defined as the way x' looks to the observer. Therefore x = ct is not a parallel construction to x' = ct'. The two equations are not analogous. In fact, if we are given that x’ = ct' (and we must be, that is one of the postulates) then x = ct’²/t. This assures that xt = x't'. Using the current equations, xx'= tt', which cannot be.
The second mistake is in assigning the variable v in the term vt. What velocity is this? You will say it is the velocity of the spaceship, in this example. But is it the velocity measured by the spaceship or by the observer? The two will measure different velocities, but we are not told which it is. The variable is undefined. Likewise the t variable in vt. Because v and t are unprimed we assume they are measured by the observer, but if the observer already has a velocity in hand, why do we need a velocity transform later on? The velocity transform of Special Relativity claims to transform a v’ into a v. But if we already have a v then what do we seek? You will say that v is the velocity of the spaceship and that the velocity transform allows us to calculate the velocity of the man walking. But shouldn’t the spaceship require transforms too, not just the man? The spaceship is moving, therefore it is not in our coordinate system, therefore by the laws of Special Relativity it must require transforms. But Special Relativity never supplies these transforms.
And this takes us to the third mistake. Gamma and the velocity transform are both generated from a conceptualization that yields two degrees of Relativity. You can see that the spaceship should require a transform itself. Then the man inside the spaceship should require a second one. The spaceship moves relative to the observer; the man moves relative to the spaceship. Relativity provides the two-degree transform but ignores the one-degree transform. In addition, Special Relativity provides the wrong transform for two degrees, as MM has shown. Its math fails because its postulate equations are incorrect, its variables are undefined, and it has only two coordinate systems when it needs three.
The final mistake is giving the spaceship in the drawing a trajectory at right angles to the observer on earth. If you will notice, the man cannot be made to walk directly away from the observer, even in his own field. His orientation relative to the observer on earth changes as time passes, so that the line x is not an accurate representation of his movement relative to the earth. The trajectory of the man would actually describe a curve in this problem. The line of equal distance from a point is a circle; therefore to remain at a constant distance from the observer on earth, the spaceship would have to orbit the observer, not go in a straight line tangent to his line of sight. This skews the whole problem. The right triangle does not have an angle of 90 degrees, for one thing, so that the Pythagorean theorem may not be used in the way it has. Furthermore, correct math will show that a spaceship passing on a tangent like this will require a variable transformation equation, one that changes every moment depending on its angle to the line of sight of the observer. A man moving on the spaceship will require even more complex transforms. The simple constant transforms of Special Relativity can only apply to movement directly away from an observer, and even there they require the corrections below.
Simplification Part Three - The Correction
It turns out that the time as measured by an observer of a moving body is simply the time of the moving body plus the time it takes for light to go from the moving body to the observing body.
t = t' + tc
tc = x'/c
x' is used in this equation, because although it would seem to be only a measurement of distance by the moving body, it happens to be equivalent to the measurement of the background by the observer. In this way it becomes the background of all three: the moving body, the light, and the observer. This is the secret information that has always existed behind the problem, although it has never come to light until now. You will say that the measurement of the background by the observer is x, but that analysis is another that has been historically incorrect. In the transformation equations of Special Relativity, x stands for—and always has stood for—the way that the observer measures the moving body. It does not stand for the way the observer measures its own lengths and distances. x is the distance that the observer calculates the body to have gone, using its data. This is not the same conceptually as a length or distance within the system of the observer.
The fact is that in SR, x' must be one of the givens of the thought problem. Einstein gives it to us by giving us v, although this has never before been clear. But if you give someone a velocity, you have given them some x over some t. This is conceptually the x that Einstein has given us: x' (although he never puts it in those terms). Of course, x' is also the variable used for length within the system of the body. This is also one of the givens or postulates of the problem, and therefore does not need to be proved.
x' = distance in moving body’s system, when measured by the moving body = distance in observer’s system when observer is measuring itself.
x = distance in moving body’s system when it is measured by the observer. This is the
body as seen by the observer.
x' thus belongs to what MM is calling a local system. Even relativists believe in the local system. It is not a return to Galileo. Feynman, for instance, calls it the proper system. (Feynman Lectures on Gravitation, p.94 "How much is the time difference at various points in space? To calculate it we compare the time rates with an absolute time separation, defined in terms of the proper times ds.")
In the local system, magnitudes are always measured from a negligible distance, so that the speed of light does not enter the equation or the measurement. In addition, light always travels in the local system. This is simply because every observer observes light in his own system. It is impossible to see light in another system. Our data arrives on electromagnetic waves, which waves must be in our system when we receive them, by a tautology. We measure everything relative to our own background, and we are stopped relative to that background. That is what makes it our background, of course. A background that is moving is a contradiction. Therefore, since light travels c relative to any unmoving background, light travels c in every local system. This means, of course, that there is a universal local system, defined by the speed of light. This universal local system, which is simply the equivalent of the classical universal system of Galileo and Newton, pertains whenever we are making measurements in our own system, by a method that does not require a transform. If you are measuring your own velocity relative to a given background, for instance, you are in the universal system. Only when you are measuring the velocity of a distant object are you no longer in the universal system. In this case you require a transform. The transform may be derived like this:
|
t = t' + (x'/c) xt = x’t’ v = x'/t = x/t' x' = v't' = vt t = t' + (v't'/c) = t'[1 + (v'/c)] t = t'/[1 – (v/c)] v = x'/[t'(1 + v'/c)] v = v’/[1 + (v’/c)] = cv'/(c + v') v' = v/[1 - (v/c)] = cv/(c - v) x = x' [1 - (v/c)] x' = x[1 + (v' /c)]
The common term (which MM has dubbed alpha) in all these transforms is
|
Alpha has long been used in optics to transform frequency from one system to another. Feynman uses the equation in his Lectures on Gravitation in a proof of gamma.
f' = f[1 + (v'/c)]
That is, he uses the correct term to prove the incorrect term. No one before me has seen that the accepted transform for frequency must be equivalent to the transformation term for one-degree Special Relativity.
Simplification Part Four - An Approaching Body, a Trajectory at an Angle
All these transforms apply only when the moving body is moving directly away from the observer. You can see that the observer measures the period of the clock of the moving body to be greater than the period measured by the body itself: t > t’. [These time variables stand for periods, not instants, as even Einstein admitted (see The Meaning of Relativity, chapter 2, eq. 22a)]. In other words, there has been a redshift. If the clocks are thought of as waves—and clocks certainly may be called waves—then the period of the clock has been stretched by its movement away from the observer. It has been redshifted.
Extending this reasoning, a clock approaching an observer must be blueshifted.
If td = period of departing object
and ta = period of approaching blinker
td = 1/ta
t = t' - x'/c
v = x'/t
v = x'/(t' - x'/c) = v'/(1 - v'/c)
v' = v/(1 + v/c)
In this way we see that a body approaching an observer will be time-contracted rather than time dilated. In other words, the observer will measure a smaller time than the body will measure for itself: t' > t. He will also measure a larger x: x > x'. This contradicts the current interpretation of SR.
For simple experimental proof of this assertion, consider binary pulsars. Pulsars are clocks in the sky, which clocks create arriving waves of data here on earth. When the pulsar is moving toward us in its orbit, its period increases. The data is blue-shifted. This directly contradicts the standard interpretation of SR, which says that all relative motion causes time dilation. Time dilation is a larger period, but the motion of the binary pulsar creates a smaller period, which is time contraction. There is no way for the standard model to answer this, since if they answer that time dilation is a smaller period, then you point to the same pulsar moving away in its orbit. We have two opposite shifts here, no matter how you define them. You can't logically define both of two opposite shifts as redshifts.
In addition, bodies moving at an angle to an observer will require complex transforms—ones that do not match either of the simple ones we have found. Trajectory must always be considered in SR. Trajectories at an angle will yield variable transforms, since the time and distance differences are not constant. These variable transforms will be dependent upon the speed, angle, and trajectory (approaching or receding) of the moving body.
Simplification Part Five - The Second-Degree Transform
To find second-degree transforms, like Einstein’s velocity transform, we must expand our problem to three coordinate systems and five sets of variables:
A = man's system
B = train's system
C = system of the embankment and observer
We need five velocity variables to solve:
1) The man's velocity relative to the train, measured by the man, v'''.
2) The man's velocity as seen from the train, v''.
3) The train's velocity relative to the embankment, measured by the train, v''''.
4) The train's velocity as seen from the embankment, v'.
5) Only then can you ask about the man's velocity as seen from the embankment, v.
Let v of A rel B (man to train) = v"
let v of B rel C (train to embankment) = v'
what is v of A rel C (man to embankment)? = v
Given v' and v'', seek v.
v''' = the velocity of A measured by A.
= v''/[1 - (v''/c)]
And we can calculate the velocity of B measured by B in the same way.
v'''' = B measured by B,
= v'/[1 - (v'/c)]
The velocity of A relative to C, if ABC is a straight line, would be
v = v'''' + v'''
1 + [(v'''' + v''')/c]
= [v'//1 - (v'/c)] + [v''//1 - (v''/c)]
1 + {[v'//1 - (v'/c)] + [v''//1 - (v''/c)]}/c
v = v' + v" - (2v'v"/c)
1 - (v'v"/c2)
Equally simple math (not shown) allows us to find a two-degree time transform, one that is not gamma:
t/t'' =
c2 - v''v'
=
1 - v''v'/c2
(c - v'')(c - v')
(1 - v''/c)(1 - v'/c)
These transforms apply only to objects moving away from an observer in a straight line. Remember that we are dealing with observation by the use of light rays. In the observation of A from C, the light rays will travel directly from A to C. They will not necessarily pass through B. B has its own light rays from A that it is dealing with. But we should only be concerned with the light rays coming to us. That is, visual observations are made directly, and indirect evidence is dangerous in relativity. We must deal only with our own light rays, the ones entering directly into our eyes. The relativity equations apply only to these rays.
This is not so clear when you are dealing with relative velocities all in the same line. In this case, the light rays do pass through B. But this will not always be the case, obviously. In second-degree transforms, the trajectories of both objects must be taken into account.
Note from Miles Mathis
First written November 1, 2000
Here at the very beginning Miles Mathis states clearly that in correcting the transformation equations of Special Relativity, he is not thereby exploding Relativity as a whole. He accepts time dilation and length contraction. He accepts the speed of light as a constant. His critique of Einstein's equations is an effort to fine tune them, not to jettison them.
He fully understands the current state of the conversation on Special Relativity. He knows that SR has met fierce resistance from "classicists" and that the scientific status quo has been forced to take a rather extreme stance against those who seem to them unable to follow the concepts and math of the theory. However, he will show that the math is subtly flawed nonetheless, and that it must be corrected in order to make the equations continue to match experiments. In that sense, this paper is an effort to bolster the theory of Special Relativity, not to tear it down. If this paper proves anything, it proves that a return to pre-Einsteinian concepts cannot be preferred.
As an olive branch to the classicists, though, he admits that the mathematical errors made by Einstein have been a large part of the problem in understanding his Relativity theory. It is no surprise, really, that it has remained impenetrable to many intelligent people. Conversations with the scientific status quo have shown that none of them understood it either. They simply had access to raw data that confirmed the theory, and that was (understandably) good enough for them. Only now that we have reached a level of precision where experiments are no longer confirming SR is there an opportunity to look again at the equations objectively, without all the name-calling and high emotion.
This paper is not a philosophical or metaphysical treatise. It is not an attempt to discredit Einstein or Special Relativity. It is not the call for a return to Newtonian physics. Nor is it the proposal of any supraluminal or trans-Einsteinian theory. It is the discovery of the actual mathematical errors in Special Relativity. Miles Mathis follows Einstein line by line and shows precisely where the mistakes are. In this, This is possibly the first. The most notorious critic of Einstein, Herbert Dingle, said (Nature, 1967) "I have enough mathematical insight to see that it is a waste of time to look for mathematical flaws in the theory."
Few, if any, have bothered to look at the basic math in the years since, believing the equations to have been already combed by the best minds of the century and proved beyond a reasonable doubt by field tests. But in the last decade, field tests have put the equations into question again. Despite this, nearly all (if not all) of the mathematical and theoretical work has gone into making these new tests fit the equations, rather than vice versa. This paper shows that the fault lies in the transformation equations and that they are easily correctable.
Specifically, this paper was written in response to the call by the Jet Propulsion Lab for help in understanding why the equations of Relativity were yielding wrong numbers in their calculations on space satellites (the so-called Pioneer anomaly). To date, no explanation has been offered for the discrepancies, despite many replies to the call for help and many theories published in Physical Review Letters and elsewhere. MM's paper is unique in that it offers new transformation equations, with which he makes predictions about the numbers generated by JPL. That is, MM has solved a concrete problem of applied mathematics, and he has the numbers to prove it.
MM first discovered the central tenets of this paper in November of 2000. The bulk of the paper was written before Thanksgiving of 2000, and it was in final form before the end of that year.
Inserted are some paragraph paper written June 2001 as a compression of the longer original paper of November 2000 that is shown below. One or the other was submitted in 2001-2002 to PRL, ADP, CERN, Nature, and JPL, where it was either refused or ignored. For example, it was submitted November 2001 to Annalen der Physik and refused January 2002. MM has the letter from Ulrich Eckern in his files. The original paper was submitted to PRL even before that, since it was refused in the summer of 2001.
Inserted here is the introduction from Miles Mathis June 2001 paper.
Special Relativity is widely considered one of the most famous physical theories in history, as well as one of the most perfect. Quantum mechanics, or QED, the only other theory that is as famous, has been corrected a countless number of times in the 20th century. In that time, Special Relativity has not been corrected once. Einstein's derivations of 1905 stand to this day. Gamma and the addition-of-velocity equation have never been corrected. They are considered uncorrectable. They underlie the final equations of four-dimensional space (Minkowski) and the field equations of General Relativity. The tensor calculus takes them as given.
However in recent decades there have been a number of discrepancies found in the use of the equations on data from both accelerators and space satellites. Physical Review Letters published several papers on the satellite problem (the so-called Pioneer Anomaly) of the Jet Propulsion Lab a few years ago. It was never solved to everyone's satisfaction, using the mechanical analyses offered. MM became convinced at that time, and remain convinced, that the problem is in the basic equations. So MM has returned to the original derivations of nearly a century ago. MM has concentrated on the algebraic derivations, ignoring the tensor calculus that was imported into the problem later.
The tensor calculus is a math designed to handle a large number of variables, using matrices and other time-saving devices. It is not a good math to use for simple conceptual problems, concerning only a few linear variables. The tensor calculus unnecessarily makes a very dense theory even more difficult. It is supremely difficult, for instance, to properly analyze the basic conceptions of the theory, which are spatial and temporal, when you don't have a time variable, labeled as such. Tensor calculus may be a necessity in the field equations of General Relativity, but in Special Relativity it is more math than the job requires. This is especially true in the initial derivations, where the velocity has no angle to the x-axis, and there are no other mathematical complications.
In its inception, the math of Special Relativity was algebra. Except for one step in "On the "Electrodynamics of Moving Bodies", Annalen der Physik, 17, 1905, Einstein's derivations of both gamma (γ) and the addition-of-velocity equation were algebraic. Even this one step of calculus was unnecessary, as Einstein proved in the appendix to his book Relativity, where he did without it. This is not surprising, since in both places the problem concerns linear uniform motion.
After studying Einstein's various algebraic derivations closely for several years, MM is now in a position to prove that his final equations, though close enough for much prediction, are not correct. He ignores one very important step, and this step completely compromises the math. Nor was this step uncovered in later emendations. All current derivations yield equations for two degrees of relativity. First-degree relativity is ignored.
This paper is MM's announcement of the discovery of First-Degree Relativity. MM rushes to add that in correcting Special Relativity, he is not proposing a return to classical mechanics. Nor is MM questioning the basis for time dilation. This paper is in no way a refutation of Relativity, as a whole, nor a dismissal of the need for transformation equations. MM simply offers subtle corrections to the existing mathematics. MM's transformation equations match Einstein's, in form and theory, but they provide small differences at high speeds and distances. This solves the Pioneer Anomaly, as well as several other outstanding problems.
The Primary Error
Relativity is caused by motion. An object in motion relative to a second object no longer shares the co-ordinate system of that object. We must therefore create two systems to explain them. Specifically, the length and time variables will differ, and at least one transformation equation will be required to go from one to the other. The transformation equation(s) must include the speed of light, since the finite speed of light is what makes them necessary in the first place. If c were infinite, then all space would be one co-ordinate system, as with Galileo. This is Einstein's set-up, which MM fully accepts. It implies that clocks and measuring rods will not match up across systems. The result is length contraction and time dilation, which MM also does not question.
In the 1905 paper, Einstein gives us two systems, K and k. K is at rest, k is moving. Then we are given a constant velocity, v—that is k relative to K (v is linear, along the x-axis). We are also given x and t in K, and ξ and τ in k. We seek the transform between them. This is all we are given involving K relative to k, but the first mistake has already been made.
What is wrong is that Einstein failed to assign the given v to either K or k. If the clocks and measuring rods in K are different from k, then K and k will measure velocity differently. That is, they must get different numbers for the velocity of k. But Einstein did not notice this. He did not notice that v, as given, is already a relative velocity. No one else has noticed this in 99 years. In this problem, we should have the velocity of k relative to K, measured from K; and the velocity of k relative to K, measured from k. One motion, two different numbers.
This is what MM calls First-Degree Relativity. We have a v and a v' now, and we need a transformation equation from one to the other. How can we get this?
First, MM clarifies the situation. He knows that some will say here that k has no velocity measured from k. Velocity is a relative term, one that requires a background against which to measure. This is true. k has no velocity relative to k. But k does have a velocity relative to K, and k can easily measure that velocity itself.
| v = velocity of k rel K as measured from K. v' = velocity of k rel K as measured from k. |
But before MM shows you the math for achieving a transform from v to v', Einstein's equations must be revisited, to see precisely what went wrong there. MM suspects that few will have the fortitude to wade through MM's new derivations until they are convinced beyond a doubt that the current equations of Einstein are faulty. Whether or not you know of the various anomalies that have arisen in experiments, MM will show here that Einstein's equations cannot possibly work, due to simple mathematical errors.
First of all, notice that Einstein has no transformation equation to go from v to v'. None at all.
The v transform of Special Relativity is
| V = v + w 1 + (vw/c2) |
This is a compound velocity, as is easily seen by counting the number of velocity variables. In order to calculate V, you must be given v and w. According to Einstein's famous thought experiment with the train, v is the same as our v above. It is the velocity of the a train going by on a platform. We are on the platform. In this case, w is the velocity of a man walking away from us in the train. V is then the velocity of the walking man relative to us on the platform. But Einstein never derives an equation to go from v to v'. This is because v' is not equivalent to any of the variables above. As you can see,
| V = velocity of man measured by platform v = velocity of train measured by platform w = velocity of man measured by (man or train?) v' = velocity of train measured by train |
Einstein has no v', so he cannot possibly calculate it. Special Relativity, as it now stands, does not recognize the existence of v'. This compromises all its equations. Put very simply, Einstein has too few coordinate systems. In the velocity transformation equation above, he has three velocity variables. But he tries to calculate these from only two coordinate systems. In order to do this he is forced to transfer variables across systems, and he does this illegally, as will be shown.
[Subsection added 10/2009] Professional physicists have ignored the above analysis, telling me that SR is known to be symmetrical, by Einstein's first postulate: "The laws of electrodynamics and optics will be valid for all frames of reference for which the equations of mechanics hold good." That is Einstein's wording of it from the 1905 paper. These physicists tell me that the starting velocity is symmetrical, which is why we have no v'.
If I measure your velocity as v, you will measure mine as v. That is true. Under that physical transform, velocity is symmetrical. But you must see that the equations of Special Relativity are not written for that specific transform. SR is not transforming your measurement of me to my measurement of you. In fact, if it were, we would need no transforms at all. If SR were really symmetrical in this way, we would need no t' or x' either. The actual transformational equations of SR are transforming local measurements into measurements at a distance, and there is no symmetry between those operations of measurement.
Yes, Einstein's postulate 1 is correct, if it is read correctly. The mechanical laws are valid in all frames, and you can take any frame you like as being at rest. In this sense, the laws are symmetrical. But if the operation of measurement is not symmetrical between these systems, then the transforms cannot be symmetrical either. That is, the laws are always symmetrical, but the “equations of mechanics” are symmetrical only when the physical operations between the systems are analogous. In transforming length and time in one system to another, the operations are not analogous. In Einstein's transformations, we choose quite freely to measure from one system or the other. Once we do, the symmetry is broken, because the measured system is not measuring us back. The transform is between “local numbers” and “measured-at-a-distance numbers.” There is no symmetry between those numbers.
This means that although Einstein's postulate 1 is still correct and valid, the velocity is not symmetrical across the transforms. Yes, there is a symmetry between “you measure my velocity” and “I measure your velocity”, but you are not measuring my velocity in the transforms. You are also not measuring my time or length or distance traveled. All the measuring is going in one direction only. For this reason, we do have two velocities from the start, v and v', and they are not the same number.
This paper for the most part exactly as it was presented to PRL in early 2001.
Abstract
In this paper Miles Mathis will show that the first equation of Special Relativity, the famous
| x' = x - vt |
is not applicable to the problem, since it is not Newton's "Principle of Relativity," nor a "Galilei transformation."
Using simple algebra, MM will then show that the equation x = ct is also not applicable, since it implies that length contraction and time dilation are mathematically in direct proportion, when they are in fact in inverse proportion. He will also show why Einstein's equations are so nearly correct, despite being arrived at by faulty math.
Next MM will correct these errors and offer new transformation equations. These new equations will be arrived at in a straightforward way, again with simple algebra. Furthermore, he will show that Einstein's transformation equation for velocity is an equation for two degrees of relativity. MM will show that there exists a velocity of one degree of relativity, and he will provide a transformation equation for it.
Next MM will then derive the corrected transformation equation for two degrees of relativity, for velocity.
Next, MM will solve the specific problem of the Jet Propulsion Lab, making a prediction for the exact amount of error in Special Relativity that leads to the faulty numbers in General Relativity.
Next, he will show that the present interpretation of Special Relativity—as applying equally to objects in all relative trajectories—is in direct conflict with other currently accepted facts, including Roemer's calculations on Jupiter's moon Io and data from the binary pulsar PSR 1913+16 (and all other pulsars and multiple stars). He will show the simple and inevitable resolution of this conflict.
Next he will prove that Lorentz made the same error as Einstein, and that this error was caused by a faulty interpretation of the Michelson-Morley interferometer. He will show that the diagram used to visualize the interferometer by Lorentz, Michelson, and every physics textbook in the 20th century is conceptually flawed. And he will show precisely where this flaw lies, mathematically, and how it led to the equations of Special Relativity—especially the Pythagorean component of gamma.
Finally, he will interpret the new equations, showing how they must change our conception of the nature of Relativity, of light, and of the operation of measurement itself.
Introduction to the Problem
Only very recently has there begun to be a general acceptance by the status quo that Special Relativity might be subtly flawed in some way. For most of the 20th century, of course, it was sacrosanct. No one in the mainstream would have thought to question it in any way. But now there is beginning to be an accumulation of data that does not fit Einstein's transformation equations precisely. The data that led me to work seriously on the problem was supplied by the Jet Propulsion Lab.
For several decades, various space satellites have been found to be acting a bit strangely. They are not where they are predicted to be according to relativistic calculations. The scientists who manage these craft have dismissed any number of explanations for the discrepancy, supplied to them by many of the best technicians in the field. But still the problem is unresolved. It has proven to be such a thorn that the JPL has even gone to the mainstream publications in the United States, begging for help. Newsweek published a major article on it in 1999.
Einstein published his paper on Special Relativity in Annalen der Physik in 1905. The book Relativity was published for general audiences in 1916.
This book and other books on Special Relativity published by Einstein have gone through many editions, but the theory itself has not changed in the last 96 years. Einstein made several predictions which were confirmed by subsequent data, and the theory quickly achieved a solidity and a fame that is unmatched in history.
MM's intention was to reformulate Newton's equations for velocity to conform to the latest facts. Light had recently been shown to have a finite and constant speed, and Einstein saw that this would affect calculations of position and velocity of measured objects. He saw that the measurement of time would be likewise affected. Lorentz had already offered a transformation equation for length, but Einstein provided a theory to contain Lorentz's ad hoc math. And Einstein also went beyond Lorentz in providing equations for time and velocity.
Maxwell was the first to propose that moving fields altered the dimensions within them. Poincare offered theoretical justification for this, and influenced both Lorentz and Einstein. To prove Maxwell's hypothesis, Michelson set up experiments in 1881 and again in 1887. By these experiments, light was shown to have a constant speed regardless of the speed of the observer. The second experiment included the famous Michelson-Morley interferometer. The interferometer (which is diagrammed in this paper) was designed to show the velocity of the earth relative to the "ether."
It was assumed that light traveled either through, or relative to, this ether; and that therefore the velocity of the earth would have to be added or subtracted from the velocity of light. But the interferometer found that the earth's velocity had no affect upon the measurement of the speed of light from any direction. This was one of the most mysterious outcomes in the history of science. In trying to explain this null set, Lorentz proposed a set of contractions and expansions that would offset the predicted measurements, bringing them into line with actual data. His fudge-factor turned out to be a now-famous term called gamma.
Not accidentally, Einstein's basic transformation term is also gamma. Einstein was working independently of Lorentz and on a different problem, but they both used the same concepts and the same math and so came to the same term.
Einstein began his derivation by postulating two co-ordinate systems, S and S'. S is the co-ordinate system of the observer. S' is the observed co-ordinate system. He then provides us with the basic equation
| x' = x - vt |
which he tells us is the Galilean transformation equation from one system to the other. This also gave him, he assumed,
| x = x' + vt |
He then produced the equations:
| x = ct x' = ct' |
to show the distance light travels in the two coordinate systems. He introduced gamma as the transformation term, as in the equation
| x' = γ(x - vt) where γ is gamma |
By substituting values among these four equations, he achieved a value for γ in terms of his other variables.
Quite simple, really. Except that he never precisely defined his terms. Not in the original paper. Not in the book. Not ever. And no one has ever questioned these terms
The mysteries of Special Relativity have been considered up to now to be inherent in the problem. We have been told that it is not comprehensible by ordinary mortals. It is subtle and complex, and all one can do is accept the paradoxes. That is all part of the fun, frankly. If it were transparent, it wouldn't be deep. This is the current wisdom, anyway.
Unfortunately, it turns out that the confusion is Einstein's (and Lorentz's and Michelson's, etc.) from the beginning. It is possible to define the terms precisely enough that all the mystery disappears. We are then left with distressingly simple equations that almost anyone can understand.
Over the last century there have been any number of lengthy critiques of Special Relativity. The bulk of these have been philosophical rather than mathematical, however. The argument about Special Relativity has split into two distinct factions. On one side is the vast majority of physicists who accept SR, due to its experimental success. On the other side are a minority who feel that time dilation makes no logical sense. Their theories therefore revert back to pre-Einsteinian physics, where things are tidier. It turns out they are both wrong.
Special Relativity is conceptually correct, in most ways. The experimental success of Einstein is no accident. Therefore the physicists who treat nay-sayers as "cranks" are correct, in the majority of cases. A return to Newtonian mechanics would be a step backward. However, Einstein did make some conceptual and mathematical errors which have never been corrected. Some of these are absurdly simple algebraic mistakes, which tend to vindicate the so-called "cranks" who believe that famous physicists don't comprehend the theory themselves.
In the early part of the century, physicists could admit this uncertainty, for the most part. Einstein himself admitted some confusion about SR up to the end. Karl Popper asked him a straightforward question about the Twin Paradox in the late '40's. He had no answer, and said so. Bohr said that only six people understood the theory, but we are not sure he meant he was one of the six. If he had fully understood it, he would have corrected it.
Until now no one has yet been able to point to the specific errors in the mathematics. Admittedly, Einstein's explanations made this quite difficult to do. And the spectacular successes of the theory acted as a sort of protective wall, keeping it from being seriously questioned. Institutions like the Jet Propulsion Lab could not publicly (or even privately) question such a fortified theory, without direct mathematical evidence. MM hopes that the following paper will begin the thaw.
Another Central Error
Part I: The Equation x' = x - vt
Einstein begins his book Relativity with a famous thought experiment.* It involves a railway embankment, a train, and a man on the train. The train moves with a constant velocity v. Later, the man also moves, with regard to the train. But for now we will limit ourselves to the train and the embankment.
Let us start with an illustration.
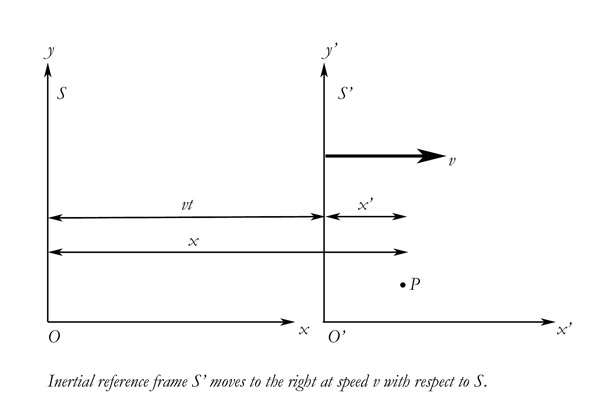
This illustration is very much like Einstein's train illustration in the book Relativity, but here the artist has tried to graph x', x, and vt. The man is at point P: meaning that x' is the x-distance from the origin to P, in S'. We, the observers, are understood to be watching from the embankment in S, the co-ordinate system to the left
In the first part of the problem, the man is not moving inside the train: x' is simply the distance of the man from the origin at t0. We are transforming the distance, not the velocity. We transform the velocity variable later, when the man also moves inside the train. Einstein makes this very clear in the paper of 1905, and it is obvious regardless. There is only one velocity variable given. If the man were moving relative to the train, we would have to be given that velocity as well, as you can see.
To go with this thought experiment, Einstein gives us this equation (p.33, Rel.) (See where it came form: Voigt),
| x' = x - vt |
In his original paper of 1905 [On the Thermodynamics of Moving Bodies], he gives the same equation. But neither there nor in the book Relativity does he say where this equation comes from. In the 1905 paper, the equation is completely mysterious; but in Relativity he gives us a clue. Einstein says, "If in the place of law of the transmission of light we had taken as our basis the tacit assumptions of the older mechanics as to the absolute nature of times and lengths, then instead of the above we should have obtained the following equations:
| x' = x - vt y' = y z' = z t' = t |
"This system of equations is often termed the 'Galilei transformation.' The Galilei transformation can be obtained from the Lorentz transformation by substituting an infinitely large value for the velocity of light c in the latter transformation."
But this is not the case. There is no such thing as a Galilei transformation equation. For Galileo and Newton, no transformation was necessary for a linear problem like this. x in S' would equal x in S. Besides, the whole universe was a single co-ordinate system for Galileo, and the train would not have been given a system of its own. There is no possibility of a prime variable of this sort in a Galilei system. The only time that two Galilei systems would have two x variables is in a case where the two systems have different origins. The equation in that case would be something like x' = x – a, where a is the distance between the two origins. In Einstein's thought problem the origins are overlapping at t0. This is one of the givens. In the paper of 1905 he states outright that the origins are equal at t0. He is not trying to calculate the distance from one system to another, he is trying to export a distance in one system to another system.
In the body of this paper MM limits his critique to Einstein's explanation in his book Relativity, and the further elucidation of that explanation in other later books. Einstein changed the math of Special Relativity several times--and not just to simplify it for general audiences. The math in his original paper of 1905 contains many more errors than the later math, which will be shown in
Appendix C. Critiquing all of Einstein's mistakes in SR, in all his various papers, would have unnecessarily lengthened this paper, and made it all but impossible to read. But those who are not convinced by MM's arguments here, or who believe that MM's math is too simple, are recommended go to the Appendix above.
This being so, the equation x' = x - vt cannot be applicable to the problem. For you can see that the true list of Galilei transformations are these.
| x' = x y' = y z' = z t' = t |
The velocity has absolutely nothing to do with a Galilei transformation. If c is infinite, then all measurers will measure equal times, distances and velocities. x' = x, v' = v. This is because there is no difference between what I see and what the train sees. Light brings me exactly the same information that it brings the train, at exactly the same time. There can be no transformation equation: not a fancy Lorentz transformation, but also not a simple transformation like x' = x - vt .

Einstein has used the wrong first equation. He has imported a Galilei transformation that is true for points on two stationary graphs and applied it to points on two graphs moving relative to each other. He assumes that the distance a between the origins after t will be vt, and that this distance will be added to x', but this is not true. For one thing, the origin of S' is not moving. If the origins were together at t0, then they are still together, since origins don't move, by definition. This is just to say that if the train started from the station at t0, then after time t the train still started from the station, which has not moved. Train stations do not move, just as origins don't move: t0' and x0' are still back at the origin, which is still back at the train station. The illustration above, which is exactly like every other illustration MM has seen, is highly misleading.
Einstein is mistaking the back end of the caboose for the origin. Look at what the equation is telling us. Let's say at t0 the back end of the caboose is at the origin of the moving system, S'. Let's also say that x' is the distance to the front of the same caboose, as measured from inside the caboose. The whole train then leaves us at the station and travels a distance given by the term vt. The equation x = x' + vt is telling us that we, back at the station, will measure the length of the caboose as "how long the caboose is, measured from the caboose" + "the distance it has gone". As if we will add the length of the train tracks to the length of the caboose!
Do you see now how utterly absurd this is? It assumes that we can't see, with our own eyes, that the back of the caboose has also traveled vt, and must therefore be subtracted from x' + vt. What we are looking for in this problem is simply "how long the caboose looks to us." This equation tells us nothing about that at all, not classically, not relativistically, nothing. It is the wrong equation. Classically, the correct equation is just x' = x. Einstein imported an equation that Galileo would have used to find the total distance from the origin to the front of the caboose after time t, and applied it to find the length of the caboose as seen from the origin. An absolutely momentous blunder.
Some will say that they agree with this last part, about the caboose, but it seems that the origin of S' does move because it is the same as the back end of the caboose. However, it is the same only if you assume that the train is not measuring its own velocity, too. If the train has no windows, and is not an active part of the experiment, then you can make the case that the back end of the caboose is the origin of S'. But as soon as the train starts measuring its own velocity, it must look out the window to achieve a background. Once it does this, its origin reverts back to the train station. If the origin of the train is the back of the train, then the train can never measure a velocity, from its own point of view. But it can, and must, for transformation equations to be found. It can, since any measurements are equally valid. It must, because transformation equations must transform something. If the train doesn't make any velocity measurements, then there is no velocity to transform.
To sum up, if light has an infinite speed, then the embankment will see both ends of any rod at the same time. The embankment will also see the back of the train and any other point on the train at the same time. So Einstein's given equation cannot be a Galilei transformation, in any sense. This mistake has never been corrected (you will find the very same equation used by Richard Feynman to prove Special Relativity in Six Not-so-Easy Pieces—92 years after Einstein). Physics textbooks still use Einstein's series of conceptual steps to prove the equations of Special Relativity.
This is the current derivation in physics textbooks:
Assume x' = x - vt
Assume that the transformation from Galilean equations to Relativistic equations will be linear. Then
Step 1: x' = γ(x - vt) where γ is the transformation term we seek.
and x = γ(x' + vt')*
Now, says Einstein (following Lorentz), light travels in these coordinate systems (S and S') in this way:
Step 2: x = ct and x' = ct'
Substituting the first equations into these equations gives us:
Step 3: ct = γ(ct' + vt') = γ(c + v)t' and
ct' = γ(ct - vt) = γ(c - v)t
If we substitute t' from the second equation into the first, we find that
Step 4: ct = γ(c + v)γ(c - v)(t/c) = γ2(c2 - v2)(t/c)
Cancel out the t on each side and solve for γ:
Step 5:
| γ = 1/√[1 - (v2/c2)] |
This is the famous transformation term gamma. But since the initial equations are not valid, the final equation is compromised. That is, gamma is false. This proof is false.
*Einstein used the equation x = γ (x' + vt)—without the t primed. But current physics textbooks have changed the notation in order to make gamma derivable with an internally consistent series of steps, as above. The math is correct; the postulates and givens aren't.
The Third Error
Part II: The Equation x = ct
This leads us to the second major problem. Everyone knows that Einstein used the Lorentz equations to find that time appeared to slow down and x appeared to get shorter. Length contraction and time dilation. But let's look for a moment at the two light equations above. The light equations Lorentz and Einstein both used:
x = ct
x' = ct'
If these are true,
then c = x/t from the first of these equations
and x' = xt'/t by substitution
so x'/x = t'/t
This means that in these equations the apparent change in x is proportional to the apparent change in t.
But when time slows down (in any system, or by any means of measurement), the period gets larger.Time slowing down implies a larger t, not a smaller t.
That is, t should appear to get larger as x appears to get smaller. Einstein even states this outright, in the book Relativity. He says (Ch.XII, p. 37) "As judged from K, the clock is moving with the velocity v ; as judged from this reference body, the time which elapses between two strokes of the clock is not one second but [γ] seconds, i.e. a somewhat larger time. As a consequence, the clock goes more slowly than when at rest." Again, he says "a somewhat larger time." Physicists have focused on the sentence after that, up to now. But time is not defined by the rate of the clock, not even by Einstein. Or stated more precisely, time is not measured that way. Relativity is primarily a theory of measurement, and so what is required is an operational definition of time. Not what time is as an abstract concept, but what time is as a measured quantity. Time is the length of the period, as Einstein flatly states here. A second is not a stroke of the clock. A second is the gap between strokes. Time is not the strokes of the clock, it is the time between strokes of the clock. As he says, a moving clock is seen by a stationary observer to have a period γt, which is larger than t. A dilated clock ticks slower because its period is longer.
[To consider this question further, see the links at the end of the paper—a discussion of this definition with several scientists and mathematicians, and a paper on the operational definition of time.]
As further proof of this very important concept, see The Meaning of Relativity again. In Chapter 2 he provides this equation (eq. 22a):
Σ Δx'v2 – c2Δt'2 = 0
Conceptually this is obviously analogous to the equation x' = ct'. Einstein is just varying his math a bit, dressing it up. The thing to notice here is the delta t. He has now made it clear that he is referring to changes in time, not instants in time. In these equations, the variable refers to the time period, not the instant in time. Which is precisely MM's point. When time slows down the period gets larger.
This being true, x and t must be in inverse proportion!
So, we should find that
x/x' = t'/t t = t'x'/x x = x't'/t
or xt = x't'
And, if x' = ct'
then c = xt/t'/t'
and x = ct' 2/t
Only if t = t' does t2/t' = t'
Einstein states that t does not equal t'
therefore x does not equal ct
Even the light equations were wrong!
Those with a knowledge of Special Relativity will interrupt here to point out that the transformation equation for x is only used to generate a length contraction equation, in the form
L' = L[(1 - v2/c2)1/2]
At least this equation is in a sensible form. But It must be pointed out that length contraction along the x-axis implies a contraction of the entire x-axis, which is a contraction of distance and which should have been given to us by the equation for x. [To get to the L equation from the x equation requires more sleight of hand, which MM will apart in Appendix B. Suffice it to say here that the x equation is not used by scientists, since none of them can say how it might be used.]
It also must be pointed out that relativistic equations are used on quanta, which have no "length" and yet distance projections are made, such as the distance a particle will travel before breaking up!
And the satellites of the Jet Propulsion Lab are slowing down in ways that are subtly unpredictable by Relativity. This is obviously a problem of distance, not of length. Nobody at JPL cares whether the satellites are getting shorter. They care whether the total distance traveled is getting shorter. So the transformation equations are being misused, simply in order to make them work at all.
Some physicists may now be shaking their heads, saying to themselves, "no, no, no." They will tell me that Einstein's first equation describes a completely different situation than the one MM has plotted and critiqued above. They will say that the equation x' = x - vt breaks down in a wholly different way.
The equation may be thought of in this way, they will say:
Since, in general, x = vt, x' = x - vt may be thought of as
(some x) = (some x) - (some x)
It corresponds to the equation in the book that Einstein offers:
w = c - v
where w is the velocity of a light ray relative to the train,
c is the speed of light as measured from the embankment,
and v is the speed of the train
In fact, Einstein implies an analogy between the two equations. Therefore we may think of the first "some x" as taking the place of w.
Therefore x' is the displacement of the man relative to the train,
vt is the displacement of the train relative to the embankment,
so x must be the displacement of the man relative to the embankment.
MM points out that this makes perfect sense except for one very important thing. The notation of the variables is imprecise and confusing. x and vt appear (because of the fact that they are both unprimed) to be in the same co-ordinate system. But they are not. A much better notation would be the following:
x" = x - v't'
This tells us that we have three co-ordinate systems—the system of the embankment, the train, and the man. And this notation stands to remind us that the given velocity is v' : the local velocity of the train. It is the velocity of the train as measured from the train, not as measured from the embankment. Einstein never differentiates between the two. He never gives us an equation to find the velocity of the train as measured from the embankment—which would be simply v. The v he derives in Chapter XIII (on Fizeau) is the velocity of a moving man on the train, but it is for two degrees of relativity. He gives us no equation (and we still have no equation) for a single degree of relativity—the relative velocity of the train.
You may say, simply set the velocity of the man to zero and run the equation. This will give the velocity of the train. But it won't, for several reasons. One, because the current Lorentz equation for velocity resolves to unity if you plug in zero for one of the given v's. It tells you that your relative velocity is equal to your given velocity—the local velocity of the train. This is no surprise, since Einstein never differentiated between the two. This becomes crystal clear if you set x" to zero in the last equation above. The equation then becomes x = v't'. This tells us nothing. It also does not give us an equation that can be manipulated by substitution in the way Einstein manipulated his equation. What MM means is: x = v't' cannot yield the term gamma
[Subsection added 10/2009] Professional physicists have ignored the above analysis, saying that SR is known to be symmetrical, by Einstein's first postulate: "The laws of electrodynamics and optics will be valid for all frames of reference for which the equations of mechanics hold good." That is Einstein's wording of it from the 1905 paper. These physicists say that the starting velocity is symmetrical, which is why we have no v'. If I measure your velocity as v, you will measure mine as v. That is true. Under that physical transform, velocity is symmetrical. But you must see that the equations of Special Relativity are not written for that specific transform. SR is not transforming your measurement of me to my measurement of you. In fact, if it were, we would need no transforms at all. If SR were really symmetrical in this way, we would need no t' or x' either. The actual transformational equations of SR are transforming local measurements into measurements at a distance, and there is no symmetry between those operations of measurement.
Yes, Einstein's postulate 1 is correct, if it is read correctly. The mechanical laws are valid in all frames, and you can take any frame you like as being at rest. In this sense, the laws are symmetrical. But if the operation of measurement is not symmetrical between these systems, then the transforms cannot be symmetrical either. That is, the laws are always symmetrical, but the “equations of mechanics” are symmetrical only when the physical operations between the systems are analogous. In transforming length and time in one system to another, the operations are not analogous. In Einstein's transformations, we choose quite freely to measure from one system or the other. Once we do, the symmetry is broken, because the measured system is not measuring us back. The transform is between “local numbers” and “measured-at-a-distance numbers.” There is no symmetry between those numbers.
This means that although Einstein's postulate 1 is still correct and valid, the velocity is not symmetrical across the transforms. Yes, there is a symmetry between “you measure my velocity” and “I measure your velocity”, but you are not measuring my velocity in the transforms. You are also not measuring my time or length or distance traveled. All the measuring is going in one direction only. For this reason, we do have two velocities from the start, v and v', and they are not the same number.
So far MM has only done a critique of the algebra of Special Relativity. But the math more commonly used in Special Relativity is calculus. It has taken this form:
Let us say the man at point P in the illustration above is moving. The velocity of the man as seen from the embankment is therefore
W = dx/dt = d[γ(x' + vt')]/dt' where γ is gamma
Differentiation yields the equation
W = v' + v
1 + vv'/c2
But the form of this differentiation assumes that W = v' + v
where v' = the velocity of the man relative to the train, and
v = the velocity of the train
If v' = 0, then the equation resolves to W = v. v is a given quantity, so the equation yields no information.
Einstein's equation for velocity tells us how fast the man appears to us to be moving, if the man is moving in the train. But if the man is not moving with regard to the train, the equation tells us nothing about the apparent velocity of the both the train and the man relative to the embankment. No one has seemed to notice that the train has a relative velocity of its own. Or, if you take the given v as the velocity of the train as seen from the embankment, then no one has noticed that the train will have a local velocity that is different from this observed velocity.
Look again at the beginning of this calculus problem as MM has stated it here. MM has stated it as Einstein and the current textbooks state it: "Let us say that the man... is moving." Notice that there is no distinction in this sentence between 1) the man moving because he is moving with regard to the train, or 2) the man moving simply because he is seated in the train, and the train is moving.
By differentiating an equation of this form, Einstein has arrived at a velocity that is in fact relative to two degrees. That is, the man relative to the train, and the train relative to the embankment. The current transformation equations do not derive a value for the relative velocity of the train. Einstein and all the physicists of the 20th century have not even noticed that this value is necessary—that it is, in fact, the value we were seeking in the first place. Nor have they noticed that physics has ended up conflating, or substituting, one value for the other. This confusion of terms has never even been noticed, much less resolved.
Part III: Lorentz, Michelson, and Pythagoras
In glossing the calculus of Special Relativity in the section above, MM is saying that Einstein's equation for velocity gives us a number as long as the man is moving with regard to the train. What MM did not say is that it gives the wrong number for that as well. It is wrong not only for the substitution and conceptual mistakes MM has already outlined, but also for the following reason.
The main feature of the Lorentz equations is the term γ. Both Lorentz and Einstein calculated gamma to be
γ = 1/√[1 - (v2/c2)]
Where did they get this? Lorentz arrived at gamma first, and his thinking was not precisely the thinking of the substitution equations MM has listed the steps for above. It is obvious from its form that gamma comes from applying the Pythagorean theorem to something. But what? Lorentz initially came up with his equations to answer the findings of the Michelson-Morley interferometer experiment. This was before Einstein proposed the theory of Special Relativity. The interferometer experiment in coverered separately in The Error of the M/M Interferometer, but a simplified illustration here will show where the Pythagorean theorem comes from. This illustration was modified from a current college physics textbook.

We have already seen two algebraic errors by Einstein in the invention and derivation of the Lorentz equations. The third—Lorentz' use of the Pythagorean theorem in deriving his original equations—arises from the problem illustrated above.
What we find in the illustration is a spaceship with a light projector inside. The projector emits a ray of light and it travels across the spaceship to a screen on the far side. The spaceship at the top is the S' system, and it illustrates the path of the light ray as seen from inside the spaceship (A). Below is illustrated how the path of the light ray would look from the outside (B), to a stationary observer on the earth. This is the S system, obviously.
We are told that the observer on earth would observe the process in B as it is illustrated. But notice that in B the light ray is moving sideways to the observer on earth. It should be obvious that our observer cannot see this light ray. No one can see a tangential light ray! We only see light rays that come into our eyes. Every light ray we see is coming directly toward us. We have no knowledge of light rays moving away from us or moving tangentially or even just missing us. To have information about the situation on this spaceship, we must be sent a signal from the ship directly toward us. In this illustration, the editors of the book are performing equations on imaginary light paths. Not observed paths, but abstractions. This is a grievous conceptual error.
To state it another way, in the A part of the illustration, measurements are being made by observation. In the B part, measurements are being made by the imagination. In A the local observer is collecting real data. If you had a person or device with the projector to collect the light rays as they returned from the screen, you could use this data to do calculations. But in B the observer is not basing his equations on collected data. He is not even collecting any data. There are no light rays coming to him, and he can have no direct data concerning the motion of the given light, or indeed the motion of the spaceship itself. In reality he would not be seeing anything. The spaceship would pass him by, unknown. He is making assumptions. He is assuming that if he could see the same light ray A sees, it would be traveling in this manner. But this is not observation, much less measurement. It is poor illustrating, poor thinking, and very poor applied math.
The Michelson-Morley interferometer was invented to to test the situation described above. You can see how the Pythagorean theorem would be used to calculate the distance light travelled in B given the distances D and L. D and L are the sides of the triangle and the path of the light ray in B is the hypotenuse. The Lorentz equations applied to the interferometer work in exactly the same way. The Lorentz transformations take us mathematically from A to B.
This would be fine if the light ray appeared from the earth to travel that path or that distance. But, as MM said, the little man does not observe that hypotenuse. It absolutely cannot be part of his data!
One of the outcomes of Einstein's relativity is that all events are local. That is, all measurements (of time, distance, etc.) are good only for the measurer. Another measurer in another place will get different measurements. And yet, by applying the Pythagorean theorem to this situation, the inventors of the visualization are attempting a non-local measurement. They are taking information obtained in a local field [specifically, the distance D, obtained by local measurement in A] and transferring it into a non-local reference field [the field in B]. This is not allowed, by the very theory they are trying to prove. In this way, the argument is circular. In order to prove that all events are local, and that time and distance are relative, they assume that quantities can be transferred from one system to another, and that D and L in A are the same as D and L in B. But quantities like D are transferable only if t and x are equivalent in both fields. Besides, D is a local measurement of the co-ordinate system A, while L is an observed distance in B, and yet they are treated exactly the same. No transformation equations are done on either one before they are plugged into the same right triangle!
MM uses the word "they," but it is not just the authors of textbooks who use these illustrations or the artists who create them who are to blame. Lorentz and Einstein do the same thing. Every illustration or conceptual analysis of this problem MM has ever seen makes this same error. The Lorentz equations came from precisely this sort of diagram or visualization, and the Michelson-Morley experiment accepts it as a given. It is the very reason that the Lorentz equations have the form they do. If the equivalent of this diagram had not been the accepted view at the time of the Michelson-Morley experiment, the Lorentz equations would not have had the form of the Pythagorean theorem. As MM will show that the true equations for simple time dilation have no Pythagorean component at all. [The equation for an object moving at an angle to an observer will use plane triangle trigonometry, but not the Pythagorean theorem].( See The Error of the M/M Interferometer to see its equivalence to the diagram above).
Part IV: New Transformation Equations
We are finally ready to derive new transformation equations. Going in, we know two things. 1) The current equations are mathematically flawed. 2) They are not far off, since they have been verified by many experiments.
We have jettisoned two of the most important equations, including the first and central one, so it is difficult to see how to start. You can see why no one has wanted to work on this problem for a century. It goes beyond a subtle tinkering. Since the end result of the transformation equations has always been the ability to derive a relative velocity from a local velocity (or other known quantities), we should ask, what do these terms mean? What is a local velocity and what is a relative velocity? It turns out that these definitions are strictly practical. That is, these velocities are determined by how we measure them. Historically we have always measured velocity by one of two methods:
1) We measure our own velocity by using a clock and by measuring our change in x relative to a known background. As an example, if we were driving in a car (but did not have a built-in speedometer) we would have to make use of mile markers. We would take note of the markers as we passed them; and then, using our on-board clock, we would calculate the velocity. Please notice that in this case we see the markers from a negligible distance. The speed of light does not affect our calculation, because we are at mile marker x when we see mile marker x.
2) We measure the velocity of an object at some distance. This measurement is arrived at in a completely different way than the first one. Usually we are given x, as in the first problem. We know x because we have already marked it off, or we have it as an accepted number from previous experiments. But t is different. We use our own clock, it is true. But, because the object is at a distance, and because light has a finite speed, we do not see the object at the same time that the object sees itself.
To make this clearer, imagine that the object is a blinking light. In this case, there are actually two events. The object blinking, and our receipt of the blink. These two events take place x distance apart, and the gap in time is the time it takes for light to travel x.
Thought problem to illustrate this.
Thought problem one:
Apparatus:
1) A blinker that blinks at a rate of one blink per second.
2) A tunnel marked off with lines, like a ruler, to indicate distance.
3) An eye, with a clock that ticks at a rate of one per second, at the beginning of the tunnel.
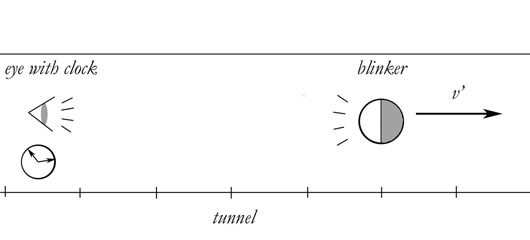
Experiment:
The blinker and the eye begin at rest, next to each other. Their blinks and ticks are exactly synchronous. The blinker then takes off and goes through the tunnel at a constant velocity. It measures its own velocity based on the number of marks it passes for each blink. It reads the marks from a negligible distance. That is, it reads the marks as it passes them .
The eye also measures the velocity of the blinker. It measures the velocity of the blinker relative to its own clock. It measures by seeing the blinks, which are blinks of visible light. The eye is given x'. It has walked off the distance in a previous experiment (or you may want assume the eye is the one who painted the lines on the tunnel).
The blinker is set on a course directly away from the eye. Assume that it reaches v' instantaneously.
Question:
Will the eye and the blinker measure the same velocity?
If not, how can the velocity measured by the eye be known given the velocity as measured by the blinker itself (and vice versa)?
Answer:
Let t' = the period of each clock, from its own vicinity. This is the period measured when the two clocks are side by side at the beginning. Notice that the blinker is a clock. Each blink is a tick of the clock.
x' = distance blinker has gone relative to tunnel marks, according to its own visual measurements.
v '= velocity blinker is going, by it's own calculation.
Let t = period that the eye sees blinks from blinker. This gives us the apparent period.
v = velocity eye calculates blinker to be going, based on visual evidence.
This is the apparent velocity.
If you are with the blinker, then you will measure your own velocity like this
v' = x'/t'
Let us say that your first blink is at the 1km mark. Your second at the 2km mark, and so on.
Obviously, your v' = 1km/s
What then is v, the velocity of the blinker as measured by the eye?
To discover this, we must first find T1. That is, when does the eye receive the first blink, according to its clock?
t = period
T = time
Well, @ T1' = 1s,
x' = 1km, so the light must travel back to the eye 1km. It takes the light 1km/c to do this. So we would expect the eye to receive blink #1 at
T1 = T1' + (x'/c) = 1.000003s
And
@ receipt of second blink, T2 = 2.000006.
@ receipt of third blink, T3 = 3.00001.
and so on.
So, for a simple blinker, the general equation would be
Tn = T n ' + (xn' /c)
t = T2 - T1
t = t' + Δx'/c
A blinker with a period of 1s and a local velocity of 1km/s will appear to have period of 1.000003s.
This period will be stable.
Notice here the difference between my equation and Einstein's. From his paper of 1905 we find t = t' + Δx'/(c - v)
Einstein has subtracted a velocity from c, which is disallowed by his own Postulate Two. The correct equation is mine, which simply drops the v variable from the equation. We not need a given velocity to start with, as MM has shown here; but if we are given one, it must be clear which system it belongs to. If it belongs to my blinker or Einstein's train, it should be labeled v'. If it belongs to my observer or Einstein's platform, then it is already a relative velocity. You can't discover it without a relative transform, as MM is presently proving (x'/c is a transform).
Now let us calculate the apparent (or relative) velocity.
v = x'/t
= x'/[t' + (x'/c)]
= .999996km/s
You may say, "Wait, why did you use x' in that equation? And why did you assume x' = 1km when you said that the light must go 1km to get back to the eye, in the time equation? You can't assume these things! Relativity tells us that the clock will slow down and that x will shrink. x should be less than x'."
MM is not assuming x' is the distance to use in the equation for apparent velocity since it is a given. The velocity of an observed object is either the given distance divided by the apparent time or the apparent distance divided by the given time. These are the only possible calculations for an observed velocity.
In the present case, v = x'/t or v = x/t' but not v = x/t
The same goes for the light ray traveling back to the eye, in the time equation. x' is simply a given here, just as c is a given. Without them, any equations—mine or Einstein's—would be useless.
If one were not given x' (or v' and t', which is the same thing), there is no way one could know it or calculate it. And there is no way one could calculate v.
Think of it this way: A train passes at night. We don't know the velocity, and we can't see the mile markers. All we can see is a pulse clock on the train. Can we know its velocity relative to us? No. The Lorentz transformations, as used up to now, can tell us nothing. We must be given a local velocity v', or we must know x'. The apparent velocity of the pulse clock is determined by its period and its speed. That is, it could be ticking slowly and going slowly, or ticking faster and going faster: in both cases it would look the same.
It is true, though, that x will look shorter to the observer, as Einstein said. But this x is not x'. Nor is it the x used in the apparent velocity equation, as MM has shown. That x is given as x'. What we are seeking for x here is the apparent distance.
It is calculated like this:
apparent x = (apparent v)t'
If you are still unclear on why MM used t' instead of t, think of it this way. What we want is to multiply the apparent velocity v by the time on our clock, right? We want to know what x is at T1 , and T2 , and so on, on our own clock. That is what it means to measure by your own clock. If you know a runner's speed, and want to calculate how far he runs in a time interval, you would not check where he was as your watch ticked 1.000003, would you? You calculate using your standard time interval, your own second hand.
You may say, "But you have defined t as the time for the eye, and t' the time for the blinker. Now you want to switch." No. I never defined t as the time for the eye. Look above. I defined both initial times as t'. The local time is t', for both the blinker and the observer. I calculated t to be the apparent period of the blinker, as measured by the eye. This does not mean that the eye's clock is ticking every 1.000003 seconds. It means, of course, that the blinker's clock looks like it is ticking every 1.000003 seconds, from the eye. But the eye's clock is ticking at a normal interval, for the eye; just as the blinker's clock is ticking at a normal interval, for the blinker. This normal interval—the rate a clock goes as seen from its own vicinity—MM has defined as t'.
Notice that if the eye's clock had a period of t, then it would not see the blinker's clock as slow. It see's the blinker's clock as having a period of t, right? If the eye's clock also had a period of t, there would be no difference. The blinker's clock is slow, relative to the eye's clock, which therefore is not slow. Very simple.
So, @ T' = 1,
v = .999996km/s.
And x = .999996km/s = .999996km.
1s
This is just what we would expect.
t has apparently slowed down. And x has apparently shrunk. That much is consistent with Einstein, at least.
But you can see that we have had to be very careful about our t's and x's and v's. You cannot just substitute an x or a t into an equation because it looks similar to another x or t. You must think about what is really happening.
So, to sum up:
The blinker's period will appear to slow down, but the period will remain stable (it will not continue to slow down further the farther away it gets).
Therefore, the velocity will also appear to be slow. If the blinker sends you a message telling you that its v' is 1km/s, then it will have appeared to slow down relative to that.
If the blinker has a length along the x-axis, then the blinker will be calculated to appear shorter, because there is an apparent contraction along the x-axis. If you measured the blinker when it was at rest next to you, then your calculation will be short relative to that.
We have found that x = vt'
and v = x'/t
so, x/t' = x'/t
and xt = x't' just as Relativity predicted.
x and t are inversely proportional. As t appears to get larger, x appears to get smaller
|
Link to an example of it use
By substituting quantities we can now easily derive the direct transformation equations, and calculate v from v' or x from x' and v':
v = x'/t = x/t' t = t' + (x'/c) = t' + (v't'/c) = t' (1 + v'/c) v = x'/[t'(1 + v'/c)] x' = v't'
v = v' 1 + (v'/c) v' = v 1 - (v/c) x = x' 1 + (v'/c) |
From June 1, 2001 paper
Or, to restate that last equation: x' = x/(1 - v/c). In this equation, you can see that the transformation term 1/(1 - v/c) can also be written c/(c - v). This is interesting because in the paper of 1905 Einstein (Relativity, Ch.XII, last page) found the transformation term to be c 2 /(c2 - v2). Einstein improperly reduced it to 1/√(1 - (v2/c2), the current value for gamma. c2/(c2 - v2) correctly reduces to 1/[1 - (v2/c2)]. There is no square root. (Historical Note: Max Born used gamma without the square root, perhaps for this reason. But this does not address the other substitution errors MM has shown.) This has also never been corrected, or even commented on3. However, it does not matter, since MM has now proved that both values for gamma are wrong. The transformation term for one degree of relativity is simply 1/(1 - v/c). This term applies when we are transforming the numbers on the train to the numbers on the platform. It does not apply to a man walking inside the train. It applies to the train itself.
You may think that the transformation term for two degrees may be gamma with or without the square root, since c2/(c2 - v2) is a sort of doubling of my term. But I will now go on to derive the velocity transform for the man walking inside the train—the velocity transform for two degrees of relativity—and in doing so I will show that gamma does not apply there either, not with the square root nor without it.
Now that we have our new equations, MM predicts this complaint: "You are assuming that t and x are absolute, before you even start. Your marked off tunnel is an absolute system of coordinates, and your t's even coincide. They may appear to be .000003s apart, but they are really the same. Relativity does not rely on these assumptions. It transcends them."
MM's answer is that he has done precisely what Einstein did. MM started with given quantities and derived unknowns from them by discovering the proper equations. You are calling my givens "absolutes," but the terminology is meaningless. They are not absolutes, they are accepted values. Einstein does not derive his relative velocities from thin air. In his transformation equations, you must have certain information to start with. MM's givens are no more absolute than his. MM's givens are exactly the same as his. If MM's elucidation of his process makes you think that these givens are absolutes, then MM can force you to admit that Einstein's givens are also absolutes.
In fact MM will do so now. Einstein says (p.18, Rel.) that the train has a given velocity v. The implication is that this velocity is a local velocity. It must be the velocity of the train, as measured from the train. He cannot mean the velocity of the train as measured from the embankment. For if he meant as measured from the embankment, then we would already be given a relative velocity, and we would not need fancy transformation equations to find it.
Einstein then shows, correctly, that the train's clock will look slow to the eye on the embankment and that the train's measuring rods will look short. And he presents the Lorentz equations for t and x. But then he never uses his relative x and t, that he derives by these equations, to calculate a relative v. Isn't this strange? He never concludes that there is a relative v that is different than the v given in the problem. He derives two t's and two x's, but never derives the second v, the relative v.
Later, he derives the Lorentz transformation for velocity, using his t and x equations (Ch.8, on Fizeau). But this is for the addition of velocities. It is for the situation in which the man on the train is moving relative to the train and the train is moving relative to the embankment (eye). You have two relative velocities and you want to find the third. This equation gives us a velocity of two degrees of relativity. The velocity that this equation yields is the velocity of the man as seen by the embankment. But this is not the same as the velocity of the train.
If Einstein had derived this relative velocity for the train as seen from the embankment, then it would have been clear that something was wrong. He would then have to admit that the given v (in equation x' = x - vt) was the velocity of the train as measured by the train. And if he admitted this, then he would have to admit that this velocity was measured relative to the tracks. And if he did that, then he would have to defend himself against the charge that he had already assumed an absolute co-ordinate system, just like MM is having to do. But in Einstein's explanation, it never comes up. He never defines his terms, and no one has ever asked him to. No one, til now, has ever asked what the given v is, precisely, and how it is determined.
The given v must be the v of the train relative to the tracks, as measured from the train. Einstein must be given this velocity before he ever starts: relative v is dependent on v'. So Einstein must have his railroad track already marked off before he can calculate his relative x and t.
He even admits this. At the top of the same page (p. 18) he says, "Of course we must refer the process of the propagation of light (and indeed every other process) to a rigid reference body (co-ordinate system)." [his parentheses]
His problem implies the existence of a pre-existing system, like my tunnel. His pre-existing system is his train track. But this system remains hidden throughout the problem. Regardless, this system—whether his or MM's—is not an "absolute." It is not an absolute in the sense of contradicting the relativity of measurement. It is a given, a postulate that allows for the calculation of unknowns.
You may be interested to know that Feynman also admitted the existence of what you are calling the "absolute" field. He called it the "proper" field, and the time the "proper time." This is just the local field, and Feynman admitted that all local fields were equivalent. They have to be in order to do any sort of calculations, of any kind.
You may say, "Yes, but there are two co-ordinate systems (S and S'). Distance in one will not be the same distance in the other. x does not equal x'. You cannot just transfer x' into your equation—as you did when the blink was traveling from the blinker to the eye—as if you already knew the distance."
Einstein did.
From second half of November 1, 2001 paper
Look at Einstein's equation for x:
x = x' + vt'
(1 - v2/c2)1/2
You can see that to calculate relative x he must be given x'. What is x'? It is local x. x measured by the train. Einstein's givens are exactly the same as mine.
My question remains, though: what is v in his equation? It can't be relative v. Einstein has not derived relative v yet. It must be local v (as measured from the train). But if this is the case, it should be labelled v', as in MM's equations.
To put it all very simply, Einstein does presume an underlying grid—like MM's marked-off tunnel—and what determines this is his given, v. As MM has shown, this v is not the velocity in S. That is what we are seeking, the relative velocity. Therefore, his given v must be the velocity in S', and should have been labelled v'. The reason this v' contains a presumption of the underlying grid is that v' entails an x'. If you are given a v' in this situation, then it is understood that you are given x'. x' is the grid. v' and x' are dependent on the grid.
[The following section is rather dense, and may be read as a footnote, or skipped with impunity. It analyses in depth the concept of the co-ordinate system, and transference of variables from one to another, using very precise notation. It will probably only confuse a first reader, and may be best saved for a second or third reading, once the rest begins to sink in.]
One may ask at this point whether the grid is part of S or S'. Or is it a third, independent, S? It seems that we are measuring both S and S' against it. And it seems that the grid would be a part of S, since the train tracks are attached to the embankment, as it were. The tracks do not move. The tracks are, in fact, connected to the embankment by rigid rods.
But the underlying grid is not strictly equivalent to S. S is an outcome of the measurement. S is created by the action of the embankment seeing the train. But the grid is not an outcome of the problem; it is a postulate of the problem. It is a precondition. The grid (MM's tunnel, Einstein's train tracks) is neither S nor S'; but it generates them both.
To be technical, a grid (or a co-ordinate system) applies only when there are no velocities or accelerations. That is why Einstein specifies a rigid reference body, a rigid co-ordinate system. Moving objects cannot be connected to grids by rigid rods.
A grid is a first-degree postulate. Meaning that it can generate x's, but not v's or a's. But neither S nor S' in this problem are first-degree postulates or grids. You can think of S and S' as second-degree co-ordinate systems—velocity grids. They are generated grids. They cannot be measured directly; they must be calculated.
Let S0 be the first-degree grid, the rigid co-ordinate system of displacement. Displacement is a primary, or first-degree, measurement. It is independent. It may be measured directly, without calculation, and without looking at any other quantity (specifically "time"). Velocity is a secondary, dependent, variable, as we know. Therefore, S and S' must be generated by S0 . S' is the velocity grid of an object as measured against S0 by the moving object itself. S is the velocity grid of an object as measured from a distance, by an observer who is not part of the object.
I believe this way of looking at it clears up much confusion. One might say it is the key to understanding the problem as introduced by Einstein. But others might complain, "Why have S0 at all? It seems like it is the same as S. All this first-degree and second-degree stuff is just folderol. Needless complication."
You can see how important it is if you ask which system, S or S', the grid belongs to. Remember that x' from above? The one we seemed to transfer willynilly from S to S'? Which co-ordinate system did it really belong to? At first it seemed to be the system of the blinker, since the blinker measured itself against it. But then it seemed to be a part of the system of the eye, since the eye and the tunnel (like the embankment and the train track) seemed to be connected to each other. It seemed like the tunnel was just an extension of the system S. The answer is that the x' doesn't really belong to either S or S'. It belongs to S0 .
This becomes clearer once we see how our two x-variables behave in their corresponding systems. The variable x that we used in our equations truly is the x in S. S is defined as how S' looks from a distance. S' is moving with regard to S. So S is how a moving grid is measured by a non-moving observer. x is the apparent displacement, due to velocity, of the whole system S' relative to S.
But x' is not really the variable x' in S'. It is not the x-variable that belongs to S'. Not in the way that x0 is the x-variable that belongs to S0 . The x-variable in S' can be measured in S' only if it is not moving. If it is moving, then it automatically becomes another system, as Einstein rightly told us. An S", say.
In other words, the x-variable in a system is used to measure non-moving things in its own system. It is a measurement of displacement or length, not a sub-measurement of velocity. x' in all our equations has not been an x of this sort. x' is a measurement by S' of its own displacement—that is, the displacement of all of S'. x' is an external number to S', as MM has said. It is a given. It is not measured by S' within S'. It is a received value. We should label it x0 , to be precise.
I will now re-run the equations for you with the proper subscripts, to clarify the preceding paragraphs. But MM has tracked the problem as MM has, leaving the S0 system out of it until now, for a reason. I believe it was necessary, so that you see the necessity for the labelling—and so that you could come to see the complications of the problem just as I did, in the same order. You must first comprehend that Einstein's given v implies the existence of the tunnel, or train tracks. Only then can you see how this sub-system—or primary system—S0 influences the whole problem. Einstein did not recognize that his given v carried with it so much baggage, and this has been what has kept Special Relativity under a cloud for almost a century.
So, to run the equations again:
We have only one moving object (the blinker), whose velocity we want to measure from a distance. To do this properly we need three co-ordinate systems. We must have S0 , S, and S'. S0 is the base system or sub-system or non-velocity system that generates the two relative velocity systems S and S'. This S0 is equivalent to the non-velocity system of the eye, but should not be confused with S, since S is the how a moving object looks to the eye. S0 is how a non-moving object looks to the eye.
Now, we are given two things.
1) The co-ordinate system S0 , whose measurements we know.
2) The rate of a clock at rest relative to S0 , which we will call t0 (even though, strictly, S0 has no time—it is a displacement grid only).
t0 = the initial period of both clocks. This is the period measured when the two clocks are side by side at the beginning—WHEN THEY ARE NOT MOVING.
x' = distance blinker has gone relative to tunnel marks, according to its own visual measurements.
v '= velocity blinker is going, by it's own calculation.
t = period that the eye sees blinks from blinker. This gives us the relative period. v = velocity eye calculates blinker to be going, based on visual evidence. This is the relative velocity.
If you are with the blinker, then you will measure your own velocity like this
v' = x'/t'
But, x' = x0 since the blinker is at x0 N when it records x'N[read x prime at the Nth measurement]]
So, in the equation v' = x'/t' we may use the displacement data from the S0 system—which we have been given.
v' = x0 /t'
Likewise, t' = t0 , since t' remains a local measurement whether the blinker is moving or not. The blinker has no velocity, relative to itself; therefore its own clock remains a constant, to itself, whether at rest or in motion.
Therefore t = t0 + (change in x0 /c)
v = x0 /t
x = v/t0
But, t0 does not = t and x0 does not = x
Now your question may be, "Isn't there another way to measure velocity? You have given two methods, two operations, for determining velocity, and they both seem to require outside information. You have shown that relative velocity is dependent on local velocity (v is dependent on v'), and that local velocity is dependent upon an external grid defined as unmoving (v' is dependent on x0 ). Isn't there a more straightforward way? What about the velocity in S0 ? Can't we just divide some x0 by some t0 (or differentiate something) and get a non-dependent number?"
No, we can't. There are no velocities in S0 . That is the whole point of Einstein's two systems. Remember, the train is moving relative to the embankment. S is the embankment, S' is the train. As soon as you have a velocity, you must have a second system, or sub-system. Einstein himself created S' to explain velocity, and he was correct to do so.
Of course you can divide x0 by t0 , if you really want to. But if you do you are back to Newton and the Galilean idea of velocity. For MM has shown that x' is really x0 . And t' was defined as local time, either in S or S'. So x0 /t0 = x'/t'. If you, as the observer, measure the blinker from a negligible distance, you will get the same value for its velocity as the blinker gets for itself. This is the common idea of velocity, and is the reason why we don't usually differentiate between your measurement of your velocity and MM's measurement of your velocity. But remember that you always see with light, even from the shortest distances. An observed velocity will always be a relative velocity, to some degree.]
From this explanation, MM thinks you can begin to see that the greatest problem with Einstein's transformation equations is that there is no equation for deriving the velocity of the train relative to the embankment. This is the central question of his thought problem, and yet he never answers it. It has gone unanswered and unnoticed for a century.
Einstein's confusion on page 18 (Rel.) buries the given velocity (MM's v') so that Einstein and every other reader has forgotten it exists. Then he conflates the velocity of the train with the velocity of the man on the train, using them interchangeably. Finally, he derives a relative velocity for the man on the train, never noticing that the train has a relative velocity of its own.
For a century we have had no equation for the train's relative velocity. And no one has missed it. Physicists now routinely use the Lorentz transformation for v as if it were a transformation for one degree of relativity. But it is not. It is a transformation for two degrees of relativity: the man to the train and the train to the eye.
Let us look at the current Lorentz transformation for velocity.
W = v' + v
1 + v'v/c2
This was obtained by differentiating the Lorentz equation for x with respect to time. But notice there are three variables here:
W is the velocity of the man as measured from the embankment
v' is the velocity of the man relative to the train, and
v is the velocity of the train relative to the embankment, measured by the train
In order to calculate W, Einstein must be given v' and v. That is a lot of information. And that information implies even more information (such as x' and x). If the man and train are sending information (light rays) to the measurer on the embankment, which allows him to calculate variables such as velocity, then the measurer can easily calculate—using his givens—what the man and train are measuring for themselves. But subsequent scientists have acted as if Einstein knew nothing about the local situation of the man and the train. As if he was getting all his information from "visual" data. As if he was deriving his equations almost literally out of thin air. He was not. His transformation equations depend upon a set of givens, just like any other transformation equations. And his givens have turned out to include what might be called "absolute" information, as MM has shown. Without this "absolute" information, no equations would be possible. Without a train track already known to both the train and the embankment, the measuring eye on the embankment could never have derived anything at all. His knowledge would be as limited as the knowledge of the man watching the pulse clock pass him by at night.
Part V: Relative Velocity of an Approaching Object
Now let us take the case where the blinker is traveling at a constant velocity toward the eye. Relativity tells us that t slows down there, too. But forgive me for not accepting that at face value.
Let us first calculate when the blinks appear to arrive, in order to get t, as in the first experiment.
At the first blink we see T1 = T1' + x'/c. Light still has x' to go, so we assume the first blink will be late relative to T1'.
At this point, you may start to think maybe Einstein was right. But be patient.
For at the next interval, x' is 1km shorter. That is, the blinker is closer by 1km at the next blink.
@ blink #2, T2 = T2' + x2'/c where x2' = x1' - 1km
@ blink #3, T3 = T3' + x3'/c where x3' = x1' - 2km
So, let's put in some numbers, and see what is happening.
Assume the blinker starts 101km away and reaches v' instantaneously.
At 101km, T' = 0
So, x1' (x' @ T' = 1) = 100km, x2' = 99km, etc.
T1 = 1 + (100km//300,000km/s)
= 1.000333...s
T2 = 2.000330s
T3 = 3.000326...s
T4 = 4.000323...s
T5 = 5.000320s
What is the period here?
t = T5 - T4 = 5.000320 - 4.000323... = .999996...s
Exactly what we should have expected.
If t(d) = period of departing blinker
and t(a) = period of approaching blinker
t(d) = 1/t(a)
The general equation is therefore
t = t' - (change in x')/c
because change in x is negative.
t = t' - x'/c
v = x'/t
v = x'/(t' - x'/c) = v'/(1 - v'/c)
v' = v/(1 + v/c)
This is what MM expected, from the Doppler effect.
But notice that it is not the same as what Einstein predicted, and what Relativity now tells us.
Time appears to speed up with objects that have a velocity approaching us.
Around 1700, the Danish astronomer Ole Roemer measured the period of Io (Jupiter's moon) and proved the above assertion. When Io is moving toward the Earth, the period appears shorter. This is known and has been accepted all along, even while Relativity has tried to tell us that all moving clocks slow down. Einstein apparently did not realize that the period of Io is a clock. Scientists have never resolved these two accepted facts.
If you cannot see Io as a clock, consider the binary pulsar PSR 1913+16. It revolves around its mate much like Io moves around Jupiter. It was discovered to be binary precisely because its pulses speeded up and slowed down, as in an orbit. It is a clock. It speeds up when it is moving toward us. This is admitted by everyone. This contradicts the current interpretation of Special Relativity.
Part VI: Relative Velocity measured at an Angle
to the Line of Sight
Now let us ask about velocities that are at an angle to the line of sight. This will be somewhat trickier than it seems, for this reason:
Notice that the apparent change in the period of a moving object is dependent on the change in x'. Therefore, if x' does not change, then the object's period will not appear to change, and it's clocks will not appear to slow or speed up.
But the line of equal distance from a stationary observer is a circle around that observer. An eye or a telescope will turn with an object moving at an angle, to allow the light rays to continue to enter the eye directly. The angle of the object, then, must be measured relative to this turning eye. You will see what MM means as we get into the experiment.
Say our blinker has an initial angle to our eye of 45o at T' = 1 and a velocity of 10,000km/s.
What is it's apparent period and apparent velocity?
We desperately need an illustration here.
@ T' = 1 (blink 1)
let x1' = 100,000km (so that we won't have the tiny fractions)
What is x2' @ T' = 2 ?
yn = v'tn' so, y1 = 10,000km
Obviously, angle L = 135o
so, x2'2= x1'2 + y12 - 2y1 x1cos135o
x2'= 107304.3036km
x3' = 115014.8996km
x4' = 123055.4375km
x5' = 131365.3465km
And, to find the apparent t, we use the equations we already have.
T1 = 1 + 100,000/300,000 = 1.333333s
T2 = 2.35768
T3 = 3.383383
T4 = 4.410185
T5 = 5.4378845
And, apparent period t @ T2 = T2 - T1 = 1.024347
@T3 = 1.025703
@T4 = 1.026802
@T5 = 1.0276995
The important thing is, it is clear that the period will appear to be getting slower as the object moves away. The apparent period is not a constant in this experiment. It starts out a bit slower than t' and then continues to get even slower. But we expect it to approach a limit at t = 1.03333. Because, at infinity, it will be moving directly away. And then it will be equivalent to our first experiment.
The blinker appears to get progressively slower, approaching a limit at t = t' + x'/c. It's apparent velocity depends on it's distance away. Its angle to the line of sight decreases as it departs.
For an object approaching at the same trajectory, the opposite applies. At infinity it has an apparent period of t = t' + x'/c. That period decreases until the object hits the tangent of its trajectory (see illustration).
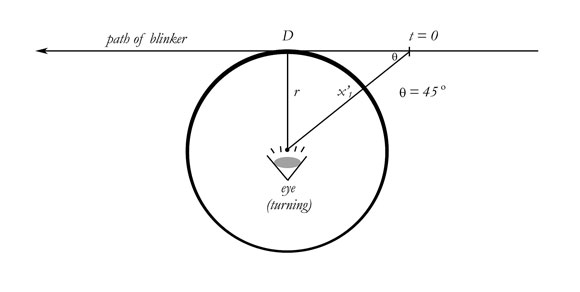
In our current problem, the blinker will hit the circle at
sin45o = r/100,000km where r is the radius of the circle
so, r = 70711km.
T= T' + .236 at the tangent.
So, with some more math, we could figure out the minimum apparent period. Obviously, it is > 1, and < 1.33.
Notice that beyond point D, the blinker becomes a departing object again.
From these thought experiments, MM thinks you can see that Special Relativity is incomplete. It states that moving clocks slow down. It does not take into account trajectory or whether the object is moving nearer or farther away. With regard to approaching objects, the Lorentz equations are flatly wrong. With regard to objects on an angled trajectory, the Lorentz equations may occasionally be a good approximation, depending on the angle at the time of measurement.
Einstein himself was never clear on the implications of his theory for objects approaching us. In conversations with Karl Popper in the 40's, for instance, Popper asked him about the twin paradox. On the question of whether the time dilation coming and going would resolve, Einstein admitted he did not know. In this particular conversation he doubted the truth of the twin paradox, but never presented any equations for or against it. My theory puts the twin paradox to rest, hopefully.
Also notice that this New Relativity implies that objects in simple orbit do not experience time dilation, since their distance from the observer does not change. MM does not have space to initiate a full discussion of this here, but those who would point to data from synchrotrons should be aware that only an observer at the center of the circle, receiving data directly (radially), would apply to MM's statement here.
Now let us go back to MM's equation for velocity. Notice how close it is to the Lorentz transformation.
MM's equation v = v'
1 + (v'/c)
Einstein's v = v' + v"
1 + (v'v"/c2)
In fact, if you think of the denominator as 1 + (v'/c)(v"/c), and you get rid of v" in the numerator and denominator, it is the same equation. MM considers this strong evidence in favor of MM's claim that MM has proceeded much like Einstein, making the same assumptions and accepting the same givens—including the given of x'. MM has just done so more explicitly
But MM claims that Einstein arrived at his equation by a rather circuitous route. It is obvious that if you take his equation for x and his equation for t and combine them without differentiation, like this
v = x/t
v = x' + v't'
(1 - v 2/c2)1/2
t' + v'x'/c2
(1 - v2/c2)1/2
v = x' + v't' = 2v't' = 2v'
t' + v'x'/c2 t'(1 + v'2/c2) 1 + v'2/c2
you do not get the same equation. Close, but not the same. All the square roots get cancelled out, but it is still the wrong equation.
But by differentiating, Einstein also fortuitously gets rid of all the square roots. The tracks are covered. And he gets an equation that now seems to work. But it only works by misuse. The process of differentiation transformed the equation into an equation for two degrees of relativity, as MM has shown. That is why it has three velocity variables. But it is now routinely used for one degree of relativity. Notice that using Einstein's algebraic derivation above would yield only two velocity variables, v and v'. But the calculus derivation yields three. Three velocity variables should imply two degrees of relativity, but Einstein doesn't realize this. And an equation, derived by differentiation, that expresses two degrees of relativity shouldn't be equivalent in output to the same equation, derived algebraically, that expresses only one degree of relativity.
Please notice how directly and cleanly MM got to his equations. My equation for t is simple and straightforward. Likewise MM's equation for x. And MM's v is simply x/t'. MM does not need the Pythagorean theorem, or any of the ridiculous illustrations and concepts that explain it. MM does not need gamma, which has proved to be an ad hoc invention, derived by a false visualization. And MM does not need calculus to solve an algebraic problem.
Furthermore, Einstein's velocity equation is not correct for two degrees of relativity either. If it is so nearly correct for one degree of relativity, MM thinks you can see that it will not work for two degrees.
To prove this, let us make quick work of the addition of relative velocities.
Part VII: The Addition of Velocities
MM is not going to derive the equations for all trajectories. MM hopes you can see that that would be very complex—much more complex than Einstein has admitted. For it depends on the trajectory of A to B and B to C. There are many possible combinations, and one equation cannot possibly cover them all. Most linear trajectories, however, will be covered by combining the three different trajectories MM has provided for a single relative velocity.
For now, let us ask about the situation where both velocities are receding from the observer in the same line.
The question is, how do you transform the Galilean equation
x/t = x'/t' + x"/t" into a relativistic equation?
Notice that, logically, you must have five sets of variables:
1) The man's velocity measured by the man.
2) The man's velocity as seen from the train.
3) The train's velocity measured by the train.
4) The train's velocity as seen from the embankment.
5) Only then can you ask about the man's velocity as seen from the embankment.
Let us say that you ignore all local events, as Relativity tries to do now (actually, it simply confuses local measurements with observed measurements, not even realizing the difference). If you are given the relative velocities to start with, then you can throw out 1) and 3) above. But you still have three sets of variables and three clocks, none of which are equivalent.
So, what if we are given the two relative velocities, 2) and 4) above?
Let v of A rel B (man to train) = v"
let v of B rel C (train to embankment = v'
what is v of A rel C (man to embankment)? = v
What one is tempted to do is just start juggling equations, which is what everyone has done up to now. But let us stop and ask what is happening. What are we really trying to find?
We are already given the relative velocities, so we do not need the equations we have discovered up to now to get them. What we need to do is visualize the problem in concrete terms. Let us start with another illustration. This always seems to help.
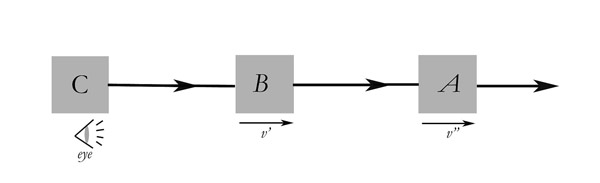
If we know how A is observed from B, will that tell us anything about how A should be observed from C?
Yes, but only indirectly. Indirectly, because remember we are dealing with observation by the use of light rays. In the observation of A from C, the light rays will travel directly from A to C. They will not necessarily pass through B. B has its own light rays from A that it is dealing with. But we should only be concerned with the light rays coming to us. That is, visual observations are made directly, and indirect evidence is dangerous in relativity. As we saw with Michelson/Morley, it can get us into trouble. We must deal only with our own light rays, the ones entering directly into our eyes. The relativity equations apply only to these rays.
This is not so clear when you are dealing with relative velocities all in the same line. In this case, the light rays do pass through B. But this will not always be the case, obviously.
Knowledge of A relative to B can give us A relative to A. With that knowledge we can calculate A relative to C. Like this:
We are given v".
Let v''' = the velocity of A measured by A.
then, v''' = v''//1 - (v''/c)
And we can calculate the velocity of B measured by B in the same way.
If v'''' = B measured by B,
then v'''' = v'//1 - (v'/c)
The velocity of A to C measured by A, if ABC is a straight line, would be
v = v'''' + v'''
1 + [(v'''' + v''')/c]
= [v'//1 - (v'/c)] + [v''//1 - (v''/c)]
1 + {[v'//1 - (v'/c)] + [v''//1 - (v''/c)]/c}
= v' + v" - (2v'v"/c)
1 - (v'v"/c2 )
If v' = v" = .4c
then, v = .57c
The Galilean transformation for this problem would have given us .8c.
The Einsteinian transformation would have given us .69c.
To see a different, more extended, derivation of this last equation, see the end of
Appendix C.
We are now in a position to critique another equation of Einstein's. That is the equation W = c - v.
On p. 18, Relativity, he defines the variables like this.
c is the velocity of light relative to the embankment.
v is the velocity of the train
W is the velocity of the light relative to the train.
He then attempts to show that this equation is incompatible with the constancy of the speed of light. He says you cannot subtract v from c, because then W would be smaller than c.
He says, "If a ray of light be sent along the embankment, we see that the tip of the ray will be transmitted with a velocity c relative to the embankment." But this is simply not true. We would see no such thing. The constancy of the speed of light requires that we measure every light ray as going c (that is, every ray that comes to us.) And that the observer on the train do likewise. It says nothing about imagining light rays that we cannot see. A light ray moving along the embankment is not part of our possible data: we make a mistake if we try to plug imagined numbers into our transformation equations. The theory of relativity cannot require that we imagine every possible light ray as going c relative to every other object. This would require stopping all the objects in the universe—except the photons. Relativity only requires that we see ourselves as stopped with regard to light. And that we calculate that every other object also sees itself as stopped.
Einstein here makes the very same mistake that Lorentz made in "visualizing" the interferometer problem. He tries to see the light from both systems at the same time, and in so doing he mixes his variables. For please notice that W in this situation is not in fact the velocity of the light relative to the train. It is the velocity of light relative to the train as imagined from the embankment. It is the embankment trying to see through the eyes of the train. But an observer on the train would not use this equation in obtaining a velocity of light relative to the train. This is because the train has no velocity relative to itself. It would not use the variable v at all. The train would measure the velocity of light directly.
The truth is that the embankment is free to imagine W as being less than c, if it wants to. It is perfectly allowed for an observer to calculate that an observed object has a velocity relative to light. It is done all the time. If nothing could be seen to move relative to light, nothing could be seen to move, period.
Part VIII: Conclusion
What does all this tell us about the nature of light? And what does a correction of Special Relativity imply about the theory of relativity as a whole? We will not see what it does to General Relativity, specifically, in this paper. But for now, we should have noticed that the speed of light is a local measurement. It is not itself a relative measurement. In this sense, Einstein really did "ride his ray of light." We know the local velocity of light, thanks to Special Relativity.
When Michelson measured the speed of light from Mt. Wilson to Mt. Baldy, he sent a light ray over and back (with a mirror). So he was coterminous with the ray at the beginning and the end. There was no distance between the observer and the observed events. Michelson had to measure light this way, using a mirror and a single point for start and finish: not because it was more expedient, but because there would be no way for him to know when the light left Mt. Wilson if he was at Mt. Baldy waiting for it, or vice versa. You might say, "He could have had a cohort at Mt. Wilson, writing it down. Or this cohort might have signaled him." But then he would have had to know the difference between t and t': as in MM's thought problem, this would require knowing c. And any signal would have been a reductio ad absurdum. What would the cohort have signaled with—a light ray?
This means that Einstein's postulate that the speed of light was an absolute turns out to be true, in the only possible way it could be. The speed of light is never an observed event, therefore it will never vary from different points of view. It never takes place at a distance. It is always coterminous, to every local observer. When you see a light ray, it is always right upon you! And that is why, when you see with light, your background always appears to be stopped. You measure the speed of light with regard to yourself, and you cannot have any velocity with regard to yourself. Your system of coordinates is also stopped with regard to you (that is what makes it yours, of course), so you will always measure light the same way. And you will always measure light the same as everyone else. They also see themselves and their coordinate systems as stopped. Their measurement of light has to be a local measurement, just like Michelson's, and every local measurement is made against a stopped background.
Remember this last point when thinking about the M/M interferometer. What was being attempted was a non-local measurement of light. Michelson/Morley were trying to "see" light from outside their own coordinate system. They only failed to see themselves moving with regard to themselves. This null set should not have been quite so shocking to the world.
And finally, if you have been paying close attention up to now, you will have noticed something else remarkable. We have seen that MM's equations are nearly identical to Einstein's. MM has followed his overall conception closely: we have time dilation and length dilation and equations that treat them similarly. Length contracts as time dilates. MM has thrown out the Pythagorean component as untenable, but this has not affected the basic content of the equations.
However, MM's thought problem adds a twist to the whole conception of time. MM started out by making t' the given, rather than t (Einstein did this, too; but not so obviously as MM did). Normally, in observing an object, we would not be given the object's own period. We would observe the period. This observed period is t. Then with c and x' we could derive the rest. This is what is done in scientific observation. But the example of the blinker has shown us more clearly that t implies a t', and that this t' applies not just to the eye, but to the blinker as well. This should have become crystal clear when we started asking whose clock was actually ticking t? The answer was, neither one. The eye saw the blinker ticking t. The blinker would have seen the eye ticking t. But each would see themselves ticking t'.
Einstein's own thought problem—which MM has simply made more transparent here—implies that in order to measure an observed velocity as dilated, one must assume that it is locally non-dilated.
Look again at Einstein's equation for t:
t = t' + v'x'/c2
(1 - v2/c2)1/2
What is t' here? According to Einstein's own illustration (p. 32, Rel.) t' is the time in S'. S' is the co-ordinate system of the train. That is, t' is the train's local time. This is just as it was in MM's thought problem.
But this is not how Special Relativity has come to be interpreted. Once all the equations are solved, Einstein and everyone since has applied t (not t') to the train. The train's clock is seen to be dilated. "It is going slow." So t now belongs to the train. Before the calculation, t' was defined as the time of the train. Afterwards t is defined as the time of the train. And then t' is forgotten (or given to the embankment). And if someone clever notices this and says, "Yes, but doesn't the train only appear to be going slow?", the modern scientists say "Don't be a classicist, we only know what we observe!"
And MM says, "We only know what we observe and what we were given in the first place."
In order to calculate the relative slowing of an observed clock, you must assume that clock is locally equivalent to your clock. What determines this equivalence? Or, to put it another way, what makes that assumption true? The speed of light itself! If the speed of light is a constant, as Einstein assumes in Special Relativity, then all local clocks will also be constant-- they will have the same period. In both MM's equations and Einstein's, c works as a local clock setter. The very form of the equation determines this. The reason both Einstein and MM could transfer that x' into our relative equations is that the constancy of light allows us to. c is the bridge from one co-ordinate system to the other. By Einstein's definition, light travels the same x in every local system. Look at the equation c = x/t : if c is a constant, and x is a constant, then t must be a constant.
Now you may ask, "If you have just proven that time is a constant in all local systems, how can you say that you agree with Einstein, or that you admire him? Isn't your paper a direct contradiction of Relativity?"
No, it isn't. What this paper shows is that Relativity is a fact at the same time that t is a constant in all local systems. This paper is not a contradiction of Relativity, it is a re-interpretation of Relativity. No one before Einstein had ever theorized that observed data were relative data, and no one had attempted to derive equations that allowed an observer to calculate the degree of relativity. These transformation equations are very valuable, and they will be even more valuable now that they are corrected and correctly interpreted.
For it is now clear that Relativity allows us to calculate local conditions from observed conditions. Up to now, it was thought that there was no direct link between your local conditions and mine. Relativity was interpreted to mean that there was only observation. "Reality" was thought to be permanently hidden, or even non-existent. But this interpretation had no basis in Relativity. When scientists used Relativity to confirm the old saw that "I cannot see through your eyes," they were forgetting that the transformation equations, read in reverse, allowed one to do just that. That is, if I can calculate x from x', then I can also calculate x' from x. x is how I see the distance. x' is how you see the distance. I can see through your eyes.
MM predicts a final complaint. Some will say, "The Lorentz equations are not even used to calculate the speed of satellites and such things. We use General Relativity and Gaussian fields and tensor calculus and other tricks way beyond that Special Relativity hubbub." My answer to that is that Einstein saw Special Relativity as the limiting case for General Relativity. The equations you are using are Einstein's and Grossmann's Riemann-Christoffel tensor equations, which themselves took the Lorentz equations as a starting point. Any correction in these equations of Special Relativity will imply a corresponding correction in General Relativity.
Einstein's mass-increase equation is the first thing that will have to be corrected. The equation m = γmo no longer pertains, since MM has demonstrated that γ is not true. Also, Minkowski's space time equations rely on the Lorentz equations. As does Einstein's gμν equation (not to mention Feynman's Diagrams, etc.) In MM's paper on gravity MM will show precisely how a corrected Special Relativity affects a corrected General Relativity.
Part IX: Inferences
First, the twin paradox relies on the assumption that all moving clocks slow down. In the second part of MM's thought experiment, MM proved that all approaching clocks actually appear to speed up, and that the rate of increase is inversely proportional to the rate of a receding clock. That is, t(receding) = 1/t(approaching). This contradicts the twin paradox.
You may ask, what of the Hafele/Keating experiment in 1971 with the atomic clocks? This experiment has been used to verify the twin paradox. But this is perhaps the most ridiculous experiment in history. It certainly proves nothing about the twin paradox with regard to Special Relativity. The scientists made absolutely no effort to limit the variables. The experiment takes place in a spinning gravitational field, with large electromagnetic variables. The clocks could be affected by any number of things, including the earth's plasma field, the sun's various fields, the moon's fields, bombardment by cosmic rays in the atmosphere, and on and on. But the most telling thing is that the airplanes carried the atomic clocks all the way around the earth. They therefore returned to the place of origin (in one sense). But this is not the same as traveling away from a point, turning around, and coming back. For one thing, it could be argued that, due to the spinning gravitational field, the point they returned to was not the point they left from, even though it was the same airport.
The twin paradox is claimed to be a logical outcome, not of General Relativity, but of Special Relativity. If all moving clocks appear to slow down, regardless of trajectory (as Special Relativity now claims), then the twin paradox would follow, regardless of any additional "paradoxes" of General Relativity. The scientists therefore should have tried to minimize the affects of gravity and acceleration. And they should have avoided traveling all the way around the earth at all costs. That makes the equations so much more difficult. A spherical gravitational field with spin and magnetic and plasma fields, intersecting at least two other major gravitational fields (sun and moon)—and then circumnavigating that field. MM has made it clear that neither Einstein nor modern physicists fully understood simple translational motion. How are they to explain a difference of 59 billionths of a second in a situation so monumentally complex?
Second, from Einstein's quote above—about the necessity of a co-ordinate system—and from the example MM mentioned before (about the train clock passing at night) we can tie Relativity to another important theory of the 20th century. MM said that a pulse clock on a night train with an unknown local period and an unknown local velocity could not plug into our equations, to give us any more knowledge. Connect this fact to Michelson's historical method of measuring the speed of light. Everyone knows that he sent a beam of light from Mt. Baldy to Mt. Wilson and timed its journey. But imagine if Michelson were not given the distance. What if he had to calculate the distance from Mt. Wilson to Mt. Baldy at the same time he was measuring the speed of light? How would he measure the distance? Send a laser over and back? You have to know c for that. Besides, that is what he is already doing. He has two unknowns and one observation.
He cannot measure x and v at the same time. Sound familiar? The Heisenberg Uncertainty Principle holds true at the macro level as well. It is not a function of Quantum Mechanics, or of statistics. Most of all it is not a philosophical truth: the HUP does not imply that v and x do not exist at the same time. It is a fundamental truth of all measurement by observation.
The only reason that the measurement of atomic particles is more indeterminate than the measurement of things on our own scale is that we can walk from Mt. Wilson to Mt. Baldy, obtain a local measurement of x', and use it in our equation. We cannot do this with atomic particles. We have no local knowledge of them. Even if we did not affect these particles with our instruments, we would still have no exact knowledge of them. We assume that the distance from Mt. Wilson to Mt. Baldy does not change spontaneously as soon as our back is turned—we assume it remains constant from one T to the next. If we stopped making this assumption, for whatever reason, then our knowledge of reality on our own scale would also become indeterminate and probabilistic. Remember, a determination of velocity in an unknown field—whether atomic or human scale—always requires two observations. First, it requires a determination of x. Then it requires an observation of how much x per how much t. As MM showed above with Michelson's determination of c, these two quantities cannot be gotten from the same observation. In our own world, we have no trouble combining the two observations. We assume continuity because we can see continuity. Every time we return to Mt. Baldy, it is in the same place, the same distance from old Mt. Wilson. But if we want to be difficult, we can always revert to a philosophy where Mt. Wilson disappears every time we turn our head or go into Pasadena for dinner. If we do this, the position of Mt. Wilson immediately acquires a probabilistic fuzziness. As Hume showed in the 18th century, nothing is really given. The odds are very low, based on past observations, that Mt. Wilson did a back flip when no one was looking; but, strictly, those are just odds. Knowledge is another thing entirely.
Let me be very clear that MM is not suggesting we stop making assumptions about Mt. Wilson. MM is not proposing the adoption of a Humean philosophy or a Bohrian quantum philosophy in regards to observing mountains. That would get us precisely nowhere. MM does think we should be consistent, though. MM thinks we should allow ourselves to make the same basic assumptions about atoms that we make about mountains. Namely, that if they send us data, they exist. And do not stop existing in between data.
Third, notice that MM's simplified equations confirm our everyday experiences, especially of the Doppler Effect. MM believe Relativity at this level, the primary level, is simply the Doppler Effect on clocks, since clocks could be considered to be waves. It is especially clear in this problem, where the clock is simply a pulse with a given frequency. A pulse with a given frequency is the definition of a wave.
Part X: A Prediction
Now let us compare our new equations with Einstein's equations, in the space satellite problem. Let us say that we are given that a satellite is traveling 12 km/s in a direct line away from us. That velocity is the velocity of the satellite by its own instruments. Let us say the satellite has been gone for a year, earth-time. Let us also say that the satellite is far enough away from any gravitational fields that General Relativity does not pertain. How far away would we expect it to be?
By MM's equation x = x' 1 + (v'/c) But first we must calculate x'. x' = v't' = (12km/s)(1 yr)(31,536,000s/yr) = 378,432,000km. The satellite measures itself to have traveled that far in one year. From the equation, we get x = 378,416,863.3km. That's how far we would "see" it to have gone in a year. That is because when we got a signal from the satellite saying "I have gone 378,432,000km" more than a year would have passed for us. It would be a year plus whatever time it took for the signal to travel that far. By the same token, the signal we receive at the 1 year mark, earth time, would not be the year-end signal for the satellite. That signal we received from the satellite on day 365 was sent out sometime earlier—when the satellite was at 378,416,863.3km. Also notice that the velocity of the satellite would appear slow, by the equation v = v' 1 + (v'/c) We would calculate the satellite to be going 11.99952km/s, from visual evidence.
|
What would we have found if we had used Einstein's transformation equations? First of all, it is difficult to see how to apply his equations to this problem. We only have one velocity, so we cannot correctly use the Lorentz transformation equation for velocity. But the JPL is applying it somehow.
V = v + w
1 + vw/c2
The only other velocity MM can imagine the scientists at JPL using is the speed of the earth in orbit. So let's assume that v = the speed of the satellite, undefined as to position of measurement; and let w = the accepted speed of the earth in orbit, again undefined. MM says undefined because current relativity makes no distinction between local velocity and measured-from-a-distance velocity. That is to say, JPL does not distinguish in its working equations between its measurement of the satellite's velocity, and the satellite's measurement of its own velocity. JPL uses the satellite's numbers for the given velocity. But Einstein's equations do not work that way, as MM has shown. He had no conception of local velocity in his theory. He took his given v to be the velocity of a moving system from the point of view of the stationary system. So proceeding like the JPL does is wrong. MM is going to follow their (likely) procedure, however, simply to discover how their discrepancies may arise. Of course, MM's equations here only take into account the Special Relativity part of the field equations. This is a correction only of the relative linear velocity: the other tensors will be affected in different ways that MM cannot discuss here.
Let us again take
v = 12,000 m/s and let
w = 30,000 m/s
V = v + w = 41,999.99983 m/s
1 + vw/c2
This is the velocity that JPL is expecting, from its own equations.
By MM's equation, above, MM would expect that JPL's instruments would be receiving this data:
v' = 12,000 m/s
v = v'
1 + (v'/c)
= 11,999.52 m/s
v + w = 41,999.52 m/s
My equations predict a slightly greater apparent slowing of the satellite than do the equations of Einstein.
Some may say, "Yes, your slowing is about 2,800 times as much as Einstein's. That is hardly what MM would called a fractional correction. The Jet Propulsion Lab reported in Newsweek that the numbers were only off by 'one ten-billionth of the effect of gravity on earth.'"
My first answer to that is that MM's slowing is 2,800 times as much only if you compare one change to another. If you compare final numbers, MM's slowing is only .00114% more than theirs. That is .0000114, without the percentage.
My second answer to that is that MM has no idea what specific equations the Jet Propulsion Lab is using to calculate the velocity of the satellites. MM would assume they are not using a simple time dilation equation like MM just did. MM would assume they are using General Relativity equations, which factor in the gravity of all the objects in the solar system. The Lorentz equations—and therefore Special Relativity—are only a small part of all the math involved. Whether MM's correction, plugged into existing GR equations, will give the Jet Propulsion Lab correct numbers, is something MM cannot say. But MM will go so far as to predict that there are other problems with the mathematical methodology at the Jet Propulsion Lab—problems that a simple fix to Special Relativity will not address.
You can see the sort of major problems that have existed unknown within the rather simple mathematics of Special Relativity for a century. (See Perihelion Precession of Mercury Explained.)
More than anything, that "one ten-billionth" claim seems to me to be little more than a tall flag announcing to all the sheer hubris of modern science. The JPL claims in these reports to have obsessed for twenty years over a number in the 10th position after the decimal point, and yet we can see from the mistakes addressed in this paper that the scientists and mathematicians of the twentieth century have been criminally unclear on the whole concept from the beginning. That Einstein made a few mistakes MM can understand; but that they have been allowed to stand uncorrected for so long, under the noses of so many "geniuses," MM cannot comprehend. The twin paradox is taught as fact to this day. As are all the other paradoxes and absurdities that have levitated not out of failures of theory, but out of failures to manipulate simple algebraic equations. MM believes it was Niels Bohr who once said that only six people really understood Relativity. Now it is apparent that he overstated that number—by six. MM does not believe for a second that JPL is actually within one ten-billionth of the truth of the matter. If they have equations that are almost working, it is sheer accident. Heuristic multiple sleight-of-hand. MM has shown that it is impossible to even apply Einstein's velocity equation to a satellite problem—in which there is only one velocity. So if the Lorentz transformation for velocity has carried over into General Relativity, as part of the JPL's calculations, it is being misused on this problem.
Also consider this: to be that accurate, JPL must know the masses of all the planets and their moons and the sun to the tenth decimal point. Not only that, but they must also estimate the total mass of the asteroid belt to the tenth decimal point. Then they must assume that there are no other unknowns. Modern science doesn't even know what gravity is, and yet they publicly congratulate themselves for measuring it to ten decimal points. The fact is, they can't know any body's gravity to ten decimal points, since G is not known to ten decimal points. (See G is the Key to the Secret of Gravity.)
"So what precisely are you predicting in this section?" you may ask. MM is predicting that his correction to the transformation equation for velocity will force the JPL, and others, to recalibrate the complex tensor calculus they are using to calculate forces, and therefore velocities. In Problems with General Relativity: Curved Space is Unnecessary, MM does a general recalibration himself, but MM cannot make numerical predictions at this time without being privy to the numbers that go into this specific problem. For example, MM admits to an ignorance concerning the mass of Jupiter to 10 decimal points. (By the way, it appears to me that measuring the mass of Jupiter from a distance requires the very equations MM has just critiqued. All information received from Jupiter arrives on electromagnetic waves, which waves are affected by Relativity, of course. If faulty equations are yielding wrong velocities for satellites, they must also be yielding wrong masses for objects in the solar system. Therefore the velocity calculations would be doubly compromised.)
Inserted Part Five Second-Degree Relativity
Inserted paper written June 2001 called Part FiveFirst MM will show why Einstein's proof does not work. In his 1905 paper he did not differentiate his ξ equation in order to find his relative velocity equation, like they do now in textbooks. He simply combined his equations algebraically, like this:
From earlier in the paper Einstein found:
γ = gamma = 1 /√(1 - v2/c2)
τ = γ(t - vx/c2)
ξ = γ(x - vt)
Now he says, if a point is moving in k,
let ξ = w(τ) where w "is a constant".
Notice two things. One, Einstein now has a point moving in k instead of a light ray. Two, he does not define this new velocity variable w at all, beyond saying it is a constant.
By substitution, he gets,
w(τ) = γ(x - vt)
wγ(t - vx/c2) = γ(x - vt) gamma cancels out
wt - wvx/c2 = x - vt
x + wvx/c2 = wt + vt
x(1 + wv/c2) = (w + v)t
x = ( w + v )t/[1 + wv/c2]
Now, watch this last step very closely. He reduces the above equation to:
V = w + v
1 + wv/c2
This is the current value for V. This equation stands to this day.
But to reduce like he did he must assume that V = x/t
We were given that w =ξ/τ
So what does v equal? v is what x over what t?
V = x/t
w =ξ/τ
v = ?/?
You may say, well maybe the x is x'. Maybe, but what is the t? He has no third t-variable anywhere, in this paper. And in later derivations, when he does have a t', he has no τ. He never has three t variables. What we need to solve for an addition of velocities, amazingly enough, is four t-variables.
t0 = the time of K from K
t = the time of the point as seen from K
t' = the time of k as seen from K
t'' = the time of k as seen from k
τ = the time of the point as seen from k.
τ' = the time of the point as seen from the point
but t" = τ' = t0
We need five x-variables
x = displacement of the point, as measured by K
x' = displacement of k, as measured by K
x" = displacement of k as measured by k.
ξ = displacement of the point, as measured by k
ξ' = displacement of the point as measured by the point
Einstein says that v is the velocity of k relative to K.
w is the velocity of a point relative to k.
V is the velocity of that point relative to K.
but to solve we also need,
w' = velocity of the point measured by the point
v' = velocity of k as measured by k
w' =ξ'/t0
v' = x"/t0
τ = t0 +ξ'/c
w =ξ'/(t0 +ξ'/c) = w'/(1 + w'/c)
w' = w/(1 - w/c)
v = x"/t'
t' = t0 + x"/c
v = x"/(t0 + x"/c) = v'/(1 + v'/c)
v' = v/(1 - v/c)
t = t0 + (ξ' + x")/c)
V = (ξ' + x")/t = (ξ' + x")/[t0 + (ξ' + x")/c)]
{eq.5} V =
v' + w'
1 + [(v' + w')/c ]
V =
v
+
w
1 - (v/c)
1 - (w/c)
v
+
w
1 +
1 - (v/c)
1 - (w/c)
c
=
v + w - (2vw/c)
1 - v/c - w/c + vw/c 2 + [v + w - (2vw/c)]/c
V =
v + w - (2vw/c)
1 - vw/c2
Just to be sure that gamma does not apply to the transformation of two degrees for t, let us find τ' in terms of v, like Einstein did.
t = t0 + (ξ' + x"/c)
w' =ξ'/t0 and v' = x"/t0
t = t0 + (w't0+ v't0)/c
w' = w/(1 - w/c) and v' = v/(1 - v/c)
t = τ' + wτ'/c(1 - w/c) + vτ'/c(1 - v/c)
t = τ'{1 + [w/c(1 - w/c)] + v/c(1 - v/c)}
t/τ' = (1 - w/c)(1 - v/c) + (1 - v/c)w/c + (1 - w/c)v/c
(1 - w/c)(1 - v/c) (1 - w/c)(1 - v/c) (1 - w/c)(1 - v/c)
= 1 - w/c - v/c + wv/c2 + w/c - wv/c2 + v/c - wv/c2
1 - w/c - v/c + wv/c2
= 1 - wv/c2
1 - w/c - v/c + wv/c2
t/τ' =
c2 - wv
=
1 - wv/c2
(c - w)(c - v)
(1 - w/c)(1 - v/c)
Similar, but not gamma. Not surprising, since gamma only has one velocity variable. But in Einstein's derivation of gamma, regarding x and t, he already had two velocities. His set-up for the addition of velocity section is exactly the same as his set-up for x and t, in the first section. The only difference is he had a light ray moving—as his second velocity—in the first part, and a point in the second part. But in both sections he is seeking equations for two degrees of relativity.
So what if we substitute the speed of light for w in the last equation above? Does it then resolve to gamma?
t/τ' = (c2 - cv)/ c2 - c2 - cv + cv
No, it resolves to infinity, just like Einstein's t-transformation. What does Einstein's addition of velocity equation resolve to if w is replaced by c?
V =
w + v
=
c + v
=
c(c + v)
=
c
1 + wv/c 2
1 + v/c
c + v
V resolves to c, in that case. The velocity of light is c whether it is measured from k or K. That is Principle 2 again. But then that means that Einstein's adding and subtracting of v from it in the tau expansion was pointless. My final equation for V also resolves to c if w is c, but MM did not get there like he did.
Now, you may say, why not use "equation 5" above? It looks very much like Einstein's equation, except that we are adding the velocities in the denominator rather than multiplying them. At most speeds this would only be a small correction to Einstein and would seem to imply that his math was not that far off.
We can't use that equation for one very important reason. The velocity variables don't match Einstein's. Mine are prime, his were not. Mine are the local velocities of k and the point. The other reason not to use equation 5 is that in most real situations we will not be given the local velocities. In using the relativity equations on quanta, for instance, the givens are not local velocities. We have no local knowledge of quanta. We would be given relative, or measured-from-a-distance, numbers to begin with, and would need an equation to determine the addition of these numbers. The famous experiment of Fizeau (explained by Einstein) is another example. We are given the speed of the liquid. But this is our determination of the speed of the liquid, not the liquid's. The given is not a local measurement of the system.
Please notice that MM's new equation for the addition of velocities gives us numbers that are very close to Einstein's in most situations. It differs from his in having another easily comprehensible term in the numerator and a minus sign instead of a plus sign in the denominator. But it may be used with confidence, since it has been derived from a thoroughly analyzed situation, as above, from five different co-ordinate systems. My first-degree equation for velocity also gives us a fraction more slowing at the speed of a space satellite, which answers the Jet Propulsion Lab's decades-old problem.
(Appendices A and C are now published in separate papers)
Appendix B: The L and t Transforms
This is the currently accepted derivation of the length equation from the x equation.
Let L = the length of a rod in S from x1 to x2.
L' = the length of the rod in S', from x1' to x2' So,
L = x2 - x1 = γ[(x2' + vt2') - (x1' + vt1')]
Since an observer in S' measures x1' and x2' at the same time, t1' = t2'
and the above equation therefore reduces to
L = γ(x2' - x1')
And, by substitution
L = γL'
The trick performed here is in the statement "since an observer in S' measures the length at the same time... t1' and t2' are the same." But t1' and t2' have nothing to do with the time when L' is measured by the observer in S'. These times are fixed. They are fixed to certain points, and are dependent upon the velocity v. That is why the t' is siting next to the v in the equation. It describes a specific x. The x's are not equal, so how can the t's be equal? We know that the velocity is constant, so if the t's are equal, the x's must be equal too. And that implies that the rod has no length in S'.
To be precise, t1' and t2' are the times when the end points of L' are seen by S' to co-oincide with external markers, if S' is measuring its own velocity. If S' is not in the process of measuring a velocity, then time will not come into the equations in S' at all. In that case, it is not that t1' and t2' are equal; it is that t1' and t2' do not exist. Time is a preparatory measurement for velocity. A measurement of length has nothing to do with time. Therefore, if you are speaking of t's in S', you must be talking about the measurement in S' of a velocity. The velocity being measured is the velocity of S' relative to S, as measured by S' (as in MM's blinker example). This is the only way you can have any transformation equation with v's in it. If you get rid of the t's in S', you thereby get rid of the whole idea of relative velocity and transformation equations. And if you get rid of the t's in S' you also get rid of the t's in S. Which leaves you with the equation x = x', which can yield no information, since it is meaningless.
This derivation, which can be found in many current textbooks, is nothing more than number juggling. The mathematicians responsible for it needed certain information at the end, and so they coerced the equations to get what they wanted. It is very bad math.
Addendum 5/03. Equally bad is the equation finessing that has gone on to get t = γt' from Einstein's t-transformation:
t = γ(t' + vx'/c2)
This is what one graduate level textbook says—"The [period] between two events that occur at the same place (x'1 = x'2) in S' is measured to be T'2 - T'1", which gives us this equation:
T2 - T1 = γ(T'2 + v x'2/c2 - T'1 - v x'1/c2)
= γ(T'2 - T'1 )
t = γt'
Absurd, because the idea of two events occuring at the same place in S' contradicts the entire thought problem of Einstein. In that case there is no motion in S'. If there is no change in x' there is no change in t'. You cannot have two events that occur at the same place and have motion, by definition.
Question by student and answer MM's Miles Mathis
Abstract: This is a question concerning variable assignments in the thought problem.
Question:
I'm reading your paper "The Discovery of First-Degree Relativity and the Refutation of Gamma and I am confused by one of your definitions and would like a clarification. In your gedanken experiment using the blinker in the tunnel you make the following definitions:
t' = the period of each clock, from its own vicinity.
x' = distance blinker has gone relative to tunnel marks, according to its (i.e. the blinker’s) own visual measurements.
v '= velocity blinker is going, by its own calculation.
You then give the following example of how the observer on the blinker measures his velocity:
If you are with the blinker, then you will measure your own velocity like this
v' = x'/t'
Let us say that your first blink is at the 1km mark. Your second at the 2km mark, and so on. Obviously, your v' = 1km/s
I am confused by the use of the tunnel marks as the measure of x’ but the blinker as the measure of time. For example, if I am stationary in the tunnel, I would measure the velocity of the blinker relative to me by measuring how long it took to for a single point on the blinker to go from one tunnel mark to the next using my local clock. On the other hand, if I am in the blinker and make a similar measurement, I would measure the time it takes a single point on the tunnel wall to move between two markers in the blinker. In other words I use my own x and my own t in both cases.
By using primes on all the variables in v’=x’/t’, your implication is that they are all from the same inertial reference frame—which they are not.
Was it your intention to measure local velocity by mixing x and t from two different frames? If so, I would appreciate it if you could explain to me why?
Then in a follow-up question:
I am not saying that you are not measuring a valid velocity. In fact, in relativity jargon you are measuring the "proper" velocity. This is defined as the ratio of distance in the other frame divided by time in the observer’s frame. What I described to you using the train as the measure of distance is the "coordinate" velocity where time and distance are both measured in the observer’s frame. The unique thing about proper time is that it has no upper limit. As your train’s speed approaches the speed of light, the blinker rate will approach zero while the rate that marks are passing on the tunnel wall will continue to increase. Clearly this means that in the limit the measured velocity approaches infinity as the speed of your train approaches c.
What is confusing is that you called the measured distance x’, which is the observer’s distance. But if it were really x’ then the measured velocity could not approach infinity as the train speed approaches c.
Answer:
OK, I see what your problem is now. You think real relativity is x/t. I have been told before that I am not doing relativity, since I am finding x'/t. But, as I say in my papers, you can't define the observed velocity as x/t, since you can't be given x, and you can't get it from the given v, either. Since all you start with in Einstein's own proof is the given v and the constant c, you can't claim that v = x/t. Here's why, once again. I will show it in three ways. First, we use my thought problem, which we have already been discussing. You are trying to use the tunnel marks as x, while I am pointing out that they are really x'. You claim the tunnel is x because it is not moving with regard to the eye or the zero point. Therefore the tunnel is part of S, not S'. But remember that it is the blinker that is seeing the marks on the tunnel from no distance. The marks on the tunnel are some very large distance from the eye. Since distance alone is enough to cause the need for transforms (time separation), it is the blinker that needs no transform on the tunnel marks. The blinker can read the marks right off the wall, as you have admitted.
But of course this means that the eye CANNOT read the marks right off the wall and call that x; if the eye reads the marks right off the wall, the eye is reading x', not x. MM has defined x' as the way the blinker sees or measures itself, and x as the way the eye sees or measures the blinker. If the eye reads the marks right off the wall, that is x', and that is because the tunnel marks are at the same distance as the blinker. Look at it this way: let us say the blinker is passing the mark “1 million km.” The marks are labeled, right on the wall in big painted letters. The eye, looking at the blinker and the tunnel with a telescope, sees the writing that says "1 million km mark". So he writes that down as his x for his v equation. But is that the way he sees or measures x, or isn't he just writing down someone else's previous measurement? The eye is not measuring that distance with a ruler, or seeing that distance, he is just writing down what someone else measured before him. It is a pre-existing number. That is why it isn't x. It is x'. For the eye to discover x, he would have to do a transform. Since the eye is ALREADY trying to calculate a transform, he cannot use x to do it.
Now the second way to show this. Let us say that you stomp your feet and say, "NO! v= x/t and that is all there is to it." Then I ask you to define x. You say that x is the distance traveled in the system S, which belongs to the eye or the zero-point or the stationary system. Well, according to relativity, that should be the x at no great distance from the eye. Since time separation causes the need for transforms (as is admitted), any point a great distance away from the eye will require transforms. So, aren't most points on the tunnel at a distance from the eye? Yes. So they should require transforms. If they require transforms, then they aren't x. You don't require transforms on your own system variables.
As MM shows, you can't be given x. You can only be given x'. Your given would be some pre-existing measurement, like my tunnel, already marked off. You have to do a transform to discover x. You can't be given x, you have to calculate it. And you don't calculate it with the equation vt, you calculate it with a transform, as MM shows.
One more run at it, for good measure. Perhaps you say, "Well, we can get x right from vt, since that is just the definition of velocity. Einstein gives us a velocity to start with, which is the velocity of the object relative to the eye." And MM says, no, if you are given a velocity, it can only be x'/t, and you seek transforms from that. v= x/t only works for objects nearby and going slowly, which is why we are finding transforms in the first place. If v=x/t worked for objects at a great distance, we wouldn't need relativity, would we?
You may say, "Well, you yourself find values for both x and t, so we can then combine them afterwards to find some v, can't we?" We can, but that velocity is pretty much meaningless. It isn't a relative velocity, since it isn't how things will look to anyone in the problem. If you put x over t, you are putting a transformed distance over a local time, which isn't anyone's data. You use a transform to go from one set of data to another, or to "normalize" an incoming set of data. But you can't "observe" x/t from a great distance, so it won't ever be your data from a distance. And you won't ever have a spacecraft sending you data in that form, since the spacecraft's data will be in the form v'=x'/t'.
Also, you are using your own methods to interpret my equations. My velocity transforms for one degree of relativity in this particular problem show that as the blinker approaches c, the eye sees its velocity approach c/2. The relative velocity is not higher than the local velocity, it is lower. Not only does the observed velocity not approach infinity, it is actually less than the real velocity. Doubtless you will think this conflicts with experimental data, but remember that the blinker is on an outbound trajectory. It is the inbound trajectory where v approaches infinity as v' approaches c. This is the situation that we find in accelerators, since the particles have to be approaching a detector.
And so MM has shown that it was not me that was "mixing" variables, it was the mainstream. This reader, following the normal but faulty procedure, was misapplying his variables, specifically the variable x. The variable assignment in this problem has not been rigorous enough, from the time of Einstein, and the faulty variable assignments were enough to cause major problems in applying the math to satellites and so on. This is what caused the Pioneer Anomaly and other anomalies.
What this means is that in the "current jargon", coordinate velocity is a ghost. It is meaningless. We can only calculate what this reader calls proper velocity. Real transforms must be performed between proper velocity (x'/t) and local velocity (x'/t'), since those are the only velocities that can come up in data. When we normalize incoming data, we are changing it from x'/t to x'/t'. We are changing it from data that has been garbled by distance and velocity into local data. The fraction x/t never comes up in relativity, since x/t only applies to nearby data. We don't do transforms on nearby data.
Now that that is cleared up, we can look at the rest of his email:
MM has no problem with the fact that the blinker is correctly seeing the marks on the tunnel because there is no distance involved. You are absolutely correct that he sees the marks on the tunnel correctly and that each mark on the tunnel that he sees represents 1 Km of distance moved IN THE STATIONARY FRAME. In other words, you are using a stationary measuring rod (the tunnel) to measure distance and a moving clock (blinker) for measuring time. Stated mathematically the velocity you are measuring is dx/dt'.
To illustrate this, let's assume that the blinker has a rest length of 1 km. Then x=x'=0 represents the back of the blinker and x=x'=1 km represents the front. Now have the same blinker moving at 1 km per second when the back of the blinker (x'=0) passes the zero mark on the tunnel (x=0). The front of the blinker is still at x'=1 km and is therefore a distance of 1 km from the origin as measured in the moving frame. But because of length contraction the front has not yet reached the first mark on the tunnel so how can its distance measured when it does reach that mark also be x'=1 km?
Well, MM has already shown that the velocity of the blinker is not dx/dt' from any vantage. From the blinker, the velocity is dx'/dt'. From the eye, the velocity is dx'/dt. But his second paragraph brings in a further complication, for it is here that he brings in length contraction. Remember that my thought problem with the blinker has nothing to do with the length of the blinker. MM is calculating how the total distance travelled is different from two vantages, not how the length of the blinker is different. Of course, they are related and proportional, but they aren't equivalent. My reader also wants to look at the first interval, which is a bit confusing, as we see. It is much cleaner to look at more distant intervals, but we will let him set our table here. His mistake is all in his last sentence. He is assuming length contraction before he has calculated it, and this assumption messes up his logic. He assumes that because the blinker is length contracted, the front of it is not at 1km. But it is. The front of the blinker is at 1km in both systems. You will say, “How can the observer see contraction then? If the front of the blinker is at 1km in both systems, no one should be able to measure contraction.” Unfortunately, that question betrays a complete misunderstanding of relativity. Relativity is not caused by the fact that the front of the blinker is at different places in the two systems, it is caused by the fact that light has to travel back to the eye from the front of the blinker. That light arrives late, so if the eye assumes all the light is arriving together, he comes to the false conclusion that the blinker is shorter than it is. We then need a transform between that false conclusion and the actual length of the blinker.
We see from this that if the blinker is very long, say a million miles long, we will need a transform even with a zero velocity. The light from the front of the blinker will arrive late, therefore we will mismeasure its length. The velocity only adds to this mismeasurement. This is also true of a very long blinker or train parked a long way away from us. With no velocity, it will already appear length contracted, since the light from the front end will arrive late. It is also true of the marks on the tunnel, which are stationary. They are parked, with no velocity. But we would still see large gaps at a large distance as contracted, due to the way light arrives. A million miles at that distance wouldn't look to us like a million miles.
You will say, if the light from the more distant points arrives late, shouldn't we see the object as longer, not shorter? No. MM has explained this in detail elsewhere, but MM will gloss it again. To see an object, we must create an image on our retina or in our instruments. This image will be made of light arriving at our eye all at the same time. That is what an image is. So we won't be able to build an image from that late arriving light, because it is late. We must join our light from the near part of the object to light from the far part of the object, so we are using older light from the far part. To arrive at our eye at the same time, it must have been emitted earlier. It has farther to go, you see, so it has to start out earlier. Since it is earlier, the far end of the object wasn't as far away as it is now. We are seeing the near end now and the far end some time in the past, you see. So the object is squashed.
And that is the answer to my reader's other question. Although the object is at the same place in both systems, it appears to be nearer in the S system, since the S system is seeing the front end with old light. My reader says, "because of length contraction the front has not yet reached the first mark on the tunnel." But the front has reached the first mark, in both systems. The observer cannot see that it has, but it has. The problem is that the observer is not seeing the front end now. He is seeing a slightly older front end.
My reader will now say, "But x is what the eye sees, right? If the eye sees old light, then so be it. The variable x must be that contracted length!" Yes, MM never disagreed with that. MM does find an x, and that is precisely what it is. My difference with standard theory is that MM does not put that x into any velocity equation. MM does not because that is not the way we measure or calculate velocity. To develop the right transforms, we must manipulate our givens in the right way, and x is never given to us. What we are given is x', so we have to develop our equations from that. The variable x can be a piece of data, but x/t cannot be a piece of data in a relativity problem, by definition. x/t is not relative, and it cannot be relativized.
Finally, this reader points out that my equations show no limit at c for the variable v. You can see that MM agrees with that, though we have to let the object approach us, not flee us as in the blinker example. The limit at c is for v', not v. There is no limit for v. Although MM admits that, he warns that that does not imply that information can travel faster than c. Even when MM lets the object approach, achieving an apparent velocity over c, no real object is going over c. Again, the calculation of v from the eye or zero-point is a false calculation. It is a miscalculation. It is the calculation of an optical or data illusion, that is all. No part of the object is outrunning light. No part of the object is beating the light back to the eye. This is very clear in my thought problem, since we find values for v over c without ever letting the object move faster than light. If the object never moves faster than light, then any message contained in the data carried by the object cannot outrun light. The object only appears to move over c, and that only because the data gets compressed. We misread the compression as a higher velocity. MM encourages you to study the problem more closely, if you don't comprehend this point. It is very clear once you understand the actual motions.
(If you get lost in this paper at any point, see "A Revaluation of Ether comparing the views of Tesla and Einstein including analysis of Airy's water-filled telescope, the Sagnac Effect, and the Hammar experiment").
Continue on to E ≠ mc2 (Gamma is Kappa) & Einstein's famous 1905 paper A Complete Re-Derivation of E=MC2 How Corrected Transforms in Special Relativity affect Mass, Momentum and Energy Equations.