The Error of the Michelson Morley interferometer
© Miles Mathis First written July 7, 2001 Addendum, July 2014: As you see, this paper is now 13 years old. Although it is correct in its analysis, the analysis could be shorter and clearer. If you get lost in this paper at any point, you may wish to consult the papers The Aberration of Starlight is an Expanding Earth and the section at the end of A Revaluaion of Ether. In the latter MM quickly dsicusses the similar Hammar experiment, the Sagnac experiment, and the Michelson-Gale-Pearson experiment. Instead of doing all the math, he just tells you what is going on directly. That should help you understand what is going on here with the M/M interferometer. You will see how a dragged ether is the opposite of an ether wind, and why no one understood that at the time (or now). Go to the last third of that paper.
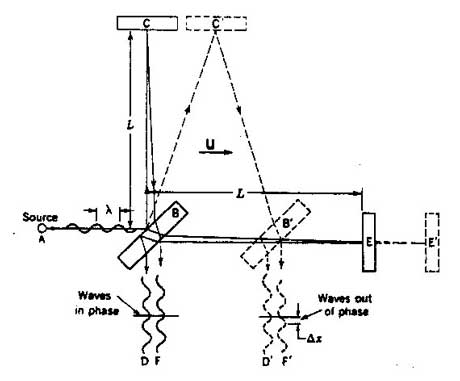
In this chapter MM will do two separate mathematical critiques of the interferometer, using two different illustrations. In the first critique he will hit the math quickly and try to make my point very briefly, in hopes of avoiding confusion and fatigue. In the second critique he will proceed much more slowly and deliberately, explaining everything and doing every mathematical step. This method may appeal to the more rigorous. The first illustration and equations are from Richard Feynman—a Nobel Prize winner and one of the most respected physicists of the 20th century. In his book Six Not-so-easy Pieces he diagrams and explains the M/M interferometer using what might be called the standard model. Here is his illustration. He says, "If the apparatus is at rest in the ether, the times should be precisely equal [from B to C and B to E], but if it is moving toward the right with velocity u, there should be a difference in the times." Then he jumps right into the math.
To show you why he is already wrong, let's look at the illustration and consider the various points of view. Notice that we already have two points of view, even though we only have one illustration. What are those points of view? Well, there is the point of view of the interferometer—or, to be more precise, the point of view of the scientist collecting data from the device. He may be thought of as sitting on the page—he is inside the illustration. Yes, of course, you say. But what is the other point of view? The other point of view is the point of view of your own eyeballs, as you look at the illustration. Not only is your point-of-view at a right angle to the point-of-view of the device and the scientist; more importantly your point-of-view is at rest, but the device is moving with regard to you. You, the scientist looking at the illustration, are outside the illustration, and the illustrated device is moving with regard to you. You are told that the device is moving. You are supposed to imagine that the page is moving to the right. We have a train and an embankment here, where we only thought we had an illustration!
For Feynman says, "Let us calculate the time required for the light to go to E and back. Let us say that the time for light to go from plate B to the mirror E is t1 and the time for the return is t2. While the light is on its way from B to the mirror [E], the apparatus moves a distance ut1 , so the light must traverse a distance L + ut1 at the speed c."
Well, from our eyeballs' point of view, looking at the illustration, yes. But from the point-of-view of the device, or of the scientist inside the illustration, no. We, looking at the illustration, conceptually see the device moving, and therefore we see the extra distance ut1. But the device does not see itself moving. It has no velocity relative to itself. No object can calculate itself as moving, in its own co-ordinate system. Any observer attached to the device or moving along with the device will see or measure the distance as L. Period. Only an observer outside the local system would see the distance as L + ut1. But the device is inside the system. The device cannot hope to measure any extra distance, or to find a phase difference at the end.
Feynman makes the same mistake regarding the distance from B to C. You and I see the distance as having a slope—it will be the hypotenuse of a right triangle with L as the base. But the device itself, or the scientist inside the illustration, would see no such thing. He would measure L as L, always.
Feynman has a slightly different conceptualization of the interferometer from the standard textbook illustration (below), but he ends up with the same math because he makes the same errors. The major error is in assigning the variable c. Feynman says the light is going c, but he does not bother to say relative to what. We assume the light must be moving c relative to the ether, since that was the historical assumption. But if the interferometer is moving to the right at velocity v, as he says, then, if we expect the interferometer to work, we expect the light will be going c - v relative to the device. And yet here Feynman says it is going c through the device. If the light is going c through the device, how can anyone expect the device to work? The device was created to measure movement relative to light, and yet Feynman says the light is moving c, which means of course that the device is not moving relative to the light. If your basic variable assignment of c tells you that the device is not moving relative to the light, you can hardly be surprised when your device tells you that your device is not moving relative to the light and refuses to give you a phase difference. You may say that light goes c relative to all observers, so that Feynman shouldn't have to specify his background. But you are mixing up your history if you say this. Special Relativity was invented to explain the interferometer, not the reverse. Historically, Michelson had no idea that c was a constant relative to all observers. How could he? He built the interferometer to find its variation, and was shocked not to find it. Feynman is explaining the historical set-up of the interferometer, a theoretical set up that has not changed since the time of Michelson. You cannot therefore claim that Feynman would include the postulates or findings of SR in his variable assignments. Feynman, like Michelson and Einstein and all the rest, should have to assign the speed of light c either 1)relative to the ether, or 2) relative to the device. Obviously, he should assign it relative to the background or ether, since Michelson was trying to measure the movement of the device (on the earth) relative to light (which was thought to be connected to the ether).
Since the whole theory of relative motion is a theory of measurement and operation, one cannot blow by the operation of measurement without asking how lengths are seen and measured. Feynman fails to precisely assign his variables. Feynman's illustration of the M/M interferometer also assumes, like every illustration before it, that the scientist collecting data from the device and the scientist looking at the illustration are the same person, or interchangable people. But in this case, the "theoretical scientist" looking down at the illustration and the "practical scientist" actually collecting data happen to be in different co-ordinate systems. They beg for a transformation equation. You need a transform simply to go from inside the illustration to outside the illustration. This is one safe that Feynman failed to crack.
Please note that this paper is a simplification by me of a paper or papers written and copyrighted by Miles Mathis on his site. I have replaced "I" and "my" with "MM" to show that he is talking. All links within the papers, not yet simplified, are linked directly to the Miles Mathis site and will appear in another tab. (It will be clear which of these are Miles Mathis originals because they will be still contain "I" and "my".) The original papers on his site are the ultimate and correct source. All contributions to his papers and ordering of his books should be made on his site.
(This paper incorporates Miles Mathis' mich paper.)

Now for a more rigorous critique. Let us begin with these two illustrations. They are modified from a recent college textbook, and may be considered typical.
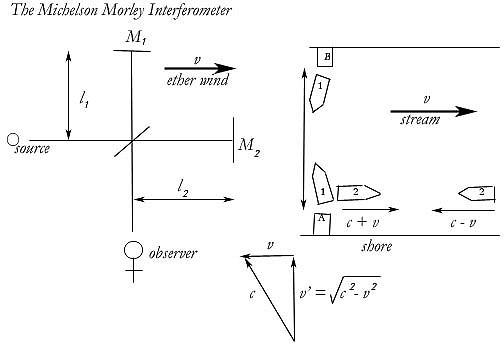
On the right side we have an illustration of two boats traveling in a stream.
Notice that we have,
1) two boats,
2) the stream and
3) the shore.
One boat goes up and back the same distance, returning to the same point on the shore. The other goes across the stream and back, also returning to the same place on shore.
The illustration on the left is of the M/M interferometer. The two illustrations are meant to be analogous. Notice that in this illustration,
1) the light rays takes the place of the boats,
2) the ether wind is the stream.
3) the interferometer and the eye are on the shore
In describing the motion of the boats relative to the shore, and the lightrays relative to the interferometer, the book uses the following equations:
t2 = time of boat 2 or lightray 2 to travel up and back
= [l2 /(c + v)] + [l2/(c – v)]
t1 = time of boat 1 or lightray 1 to travel up and back
The book says that boat 1 “must head at angle upstream” in order to reach wharf B. The book assumes that the velocity in this direction is c, and that the stream, at velocity v, will pull it back into line. This gives us a velocity v’ directly across the stream, and v’ may be found by the Pythagorean theorem:
v’ = (c 2 - v2)1/2
t1 = 2l1/(c2 - v2)1/2
The “fringe effect” is therefore the difference in t2 and t1.
The book uses this math and these steps in order to mirror the expected findings of Michelson and the other scientists of his time. This is in fact the fringe effect that was expected when the experiment was actually run. Therefore this conceptualization of the problem is very much like the conceptualization that was accepted at the time, and that is still accepted.
However, it is again completely compromised. Both the math and the conceptual assumptions are faulty. To show precisely where the mistakes are here, MM must first offer his own analogy, one that is completely different than the boats in the stream analogy. Once we find the correct equations we may return to the boats and see what went wrong.
My analogy will be two people walking in an airplane. Let us say you have two men in the cabin of an airplane. The cabin is simply a square room, 10 meters by 10 meters, say. The men are standing in one corner. Let us say they are standing on the same spot (you could say, to be more precise, that they both must push buttons that send light signals to an outside observer, and that these light signals are exactly equivalent: exactly the same distance from the observer.) Let us also say that the airplane is moving at a constant velocity directly away from the observer. Like this:
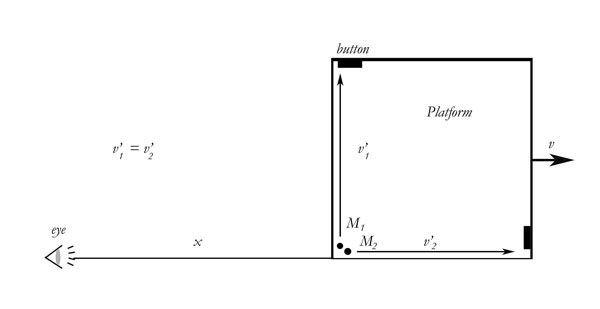
Let us go into the cabin with the men for a moment. From there, the two men move at right angles to each other. One walks 10 meters to the wall of the cabin and back. The other walks the same distance to the other wall and back. On the wall of the cabin, in each direction, is a button, for each man. This button also sends a light signal to the observer, to indicate that the man is there. The men walk at the same speed relative to the cabin. v1' = v2'. They do everything the same. What they see is that they touch the far buttons at the same time, and that they return at the same time and push the final buttons at the same time.
The question now, of course, is what does the observer see? Another way of asking this is to ask, "Will a moving airplane yield different equations from an airplane that is not moving?" In Galilean coordinate systems, where light has an infinite speed, the observer would be expected to see just what the men see. By Einstein's equations, the observer would not. How would they be expected to differ? They would be expected to differ at all points except these: They would both see the men together at the beginning and at the end. Both light signals travel the same distance from the end to the observer; the men are side by side. If they are there together, not even Relativity or an interferometer can separate them.
It is true that by Einstein's equations, we would expect the total time for both walks to appear longer for the observer than for the men. Let t0 = the time when the men depart, when they together push the signal buttons to indicate the beginning. Let tE = the time when they return and push the same buttons. The two light signals from tE have farther to go than the signals from t0, so the elapsed time between the signals will be greater.
And it is true that the observer would not see the men reach their far walls at the same time. They would be different total distances away from the observer, and the light signals would arrive slightly staggered. All t's between t0 and tE would be different for the observer than for the men. But at tE the men themselves and the observer would find them together.
This is where we go back to the interferometer. If the two light rays reach the central mirror at the same time, they must return to it at the same time, no matter where they are observed from. No matter what they may have appeared to do from the central mirror to the outside mirrors, they must return at the same time.
This is true even according to Einstein. Einstein said that any reference frame moving at constant velocity acted like a reference frame that was not moving at all. He agreed with Galileo and Newton on this. A reference frame moving at constant velocity felt no forces, and could make a valid argument that it was not moving at all. That is what Relativity means.
So, imagine you are one of the men. You do not think your cabin is moving. You feel no forces. When you walk, you are not heading slightly upstream or downstream, like the boat crossing the river, in order to hold a straight line. You are not leaning or making any adjustments. You are walking just like a person walks on an airplane, normally. Two people walking at right angles on an airplane will not get out of sync, no matter how fast the plane is going. They will appear to, from the earth, if they are going really fast; but even then they will be seen to return to the same point if they left from the same point.
You may say, "How can you be so sure? Einstein showed that simultaneity was not an absolute. Just because these men see themselves as simultaneous does not necessarily mean the eye will."
MM is not saying that all things that appear simultaneous in one field will look simultaneous in another. MM agrees with Einstein's argument on simultaneity, for the most part. But in this particular problem, the eye must see them together at the end. In Einstein's example (to disprove simultaneity), the eye is moving toward one event and away from another. This causes the appearance of non-simultaneity. But the eye in this problem is not. The two events at tE are not only simultaneous, they are also co-terminous. That is, they take place at the same spot. They simply cannot be separated by Relativity.
To prove this once and for all, let us now do the math. If the cabin has no velocity, the math is simple. Each man is going v’, the distance is given as the same, therefore the times are equal. But let us do the math if the cabin is moving relative to the observer. At first, man 2 is traveling v’ directly away from the observer, and the airplane is also traveling away from the observer at v. Therefore he is traveling v’ + v. But we must be more precise than that.
v’ = velocity of man relative to cabin
v = velocity of cabin relative to observer, measured by the cabin, not by the observer.
If we use the velocity of the cabin relative to the observer, as measured from the observer, we will have to do a transform on it due to the finite speed of light, which we want to avoid. v and v’ cannot be added together in the same equation unless they are measurement from the same coordinate system. So we must imagine ourselves in the cabin with men, making measurements from there. We are calculating our own velocity relative to the observer, just as a car would measure its velocity relative to mile markers.
Since the sum v + v’ expresses a velocity relative to the observer, we must now find a distance that is relative to the observer. We know that the distance traveled relative to the cabin is 10m; but while the man was walking that distance, the wall moved a certain distance away from the observer. Therefore the total distance must be l2 + y2A.
y2A = vt2A
t2A = (l2 + vt2A )/(v’ + v)
= l2/v’
Returning, man 2 will travel v’ – v, and the wall will approach him at v, traveling a distance y2B .
y2B = vt2B
t2B = (l2 - vt2B )/(v’ - v)
= l2/v’
t2 = 2l2/v’
No change from the calculations done when the cabin was not moving. Everything resolves. What about for man 1?
Man 1 also has a velocity v’ relative to the cabin. But v is perpendicular to v’. This gives man 1 a resultant velocity relative to the observer as
w = (v’2 + v2) 1/2
Man 1’s button on the wall has also moved a distance y 1A
y1A = vt1A
Let d = resultant distance man 1 travels outbound
d = (l12 + y1A2) 1/2 = (l12 + v 2 t1A2)1/2
t1 = 2d/w
= 2(l12 + v2t1A2) 1/2/(v’2 + v2)1/2
v’2t12 + v2t12 = 4l12 + 4v2t1A2
t1 = 2t1A
t1 = 2l1/v’
Once again, no change. No fringe effect. These calculations yield the same numbers whether the cabin is moving or whether it has a constant velocity. We could also do the calculations from the observer if we wanted. It would be more complicated since we would be doing transforms on all the numbers, but it would not affect the outcome.
Now, the question is, which analogy, mine or the boats, really applies to light in the interferometer? Let’s look at that problem again, keeping in mind what we have just learned. First of all, can we make the interferometer analogous to my airplane example? Yes: the ether wind is going v relative to the interferometer, therefore the interferometer is going –v relative to the wind. So in the first part of the problem the light is approaching M2 at c and M2 is approaching the light at –v. The distance the light must travel from the central mirror to M 2 is l2 – y2A.
y2A = the distance M2 travels relative to the ether, in the time t2A.
We cannot simply use l2 as the distance, like the book does. Since the light is being measured against the ether wind (c is relative to the ether wind), then we must look at M2 against the ether wind as well.
t2A = (l2 – y2A)/(c – v)
On the return to the central mirror, this will be the equation
t2B = (l2 + y2B)/(c + v)
Hopefully you can already see that t2A = t2B = l2/c, just as on our airplane.
One of the conceptual difficulties is that the book gives v to the ether wind instead of to the interferometer. It does so to make the analogy to the boats seem tighter. But no one ever thought (historically) that there was an ether wind. There was thought to be an ether, but the assumption was that the earth was moving relative to it, not vice versa. An ether would have to be the background of everything, and therefore could not possibly be moving. You can see that if we give v to the interferometer, in the opposite direction of the wind, it clears up many of the conceptual problems.
MM has heard the complaint at this juncture that if M2 and the lightray are moving toward each other, how can the the velocities be subtracted? Shouldn’t they be going c + v? When two cars are moving toward each other, you add the velocities, right? Yes, but that is to find the velocity of the cars relative to each other. We are doing a vector addition here and must take note of the directions of the velocities. Besides, we are not calculating, at this point in the problem, the velocity of the light relative to the mirror, or vice versa. We are measuring the resultant velocity of the two relative to the ether wind.
If this is not clear, look at boat 2 going upstream, in the other example. It is going c against the current and the current is going v against it. So you could say that the boat is going c + v relative to the current. But that is not what is being calculated there. It is correctly described as c – v. Or go back to my airplane example. When man 2 is walking back toward the observer, the wall is approaching him and he is approaching the wall. But we find that v’ – v. We are not calculating the velocity of the man relative to the wall, we are calculating the resultant velocity of both of them relative to the observer. In the other direction, it was clear why the velocity of the man was being added to the velocity of the airplane, since they were both moving away from the observer. You can hardly argue that they must be added in both directions.
Now let us look at M1 of the interferometer. Part of the light is reflected by the central mirror and heads toward M1. Like the other ray of light, it has a velocity of c relative to the ether. It is reflected at a 90o angle, relative to the source. But from the point of view of the ether, it looks like it now has a backward component –v. Locally, it doesn’t. But from the ether, it does. Since c is being measured relative to the ether, we must look at M1 relative to the ether, too.
The resultant velocity of the lightray is v’2 = (-v)2 + c2
The distance it appears to go, relative to the ether, is
d = (l12 + y1A2)1/2 = (l12 + v2t1A2) 1/2
We are repeating the steps of the airplane problem, so MM hopes the analogy is already obvious. According to my math, the interferometer should not have expected any fringe effect. And this is not because MM has used the findings of Relativity since no transforms were preformed on any of the variables. MM is only correcting the math and concepts of Michelson and his contemporaries (which, unfortunately, are still used by the status quo).
Of course there is one last way to solve, and it is the easiest. You can get rid of the ether altogether. You then just measure the interferometer and the light directly against each other. In that case you do add the velocities: c + v. The light is moving that fast relative to the machine, or vice versa. But not both. If you give the whole velocity to the light, then the interferometer is stationary throughout the problem and there is no ether wind. The light is reflected at c + v in both directions, from all mirrors, and goes that speed throughout the interferometer. Obviously, in this case there is no possibility of a fringe effect. The light never goes c – v in any part of the experiment. If we assign c + v to the light in the first part of the experiment, then the interferometer is not moving at that time. If it is not moving in the first part, why would it move in the second part? Consider the two cars moving toward each other again. If you ask how fast they are going relative to each other, then the quantity you arrive at, v + v’, you must assign to one of the cars. The other car then becomes the stationary coordinate system. The first car moves v + v’ relative to it, and it does not move. Nothing in the background moves either. You do not retain some sort of background “wind,” that explains why v’ is added to v. In the beginning, you could have explained the relative movement of one of the cars as the movement of a background wind, like the ether wind. But once you give one of the cars both velocities, this conceptual wind disappears.
This is why one should never diagram a background as moving, in an illustration. Human beings see things against backgrounds that are not moving. That is what makes them backgrounds. A moving background is a contradiction, in a very important sense. It is highly confusing to label a background as having a velocity, in a drawing. It is very difficult to conceptualize, as we have seen. It is always much better to give the velocities to the objects. The interferometer should have been given the velocity from the beginning, both to solve this problem, and because that is what is thought to be happening in real life.
There is one last problem to solve. Where does the analogy to the boats fail? It is clear where the analogy to boat 1 fails, since the light ray is not “heading upstream” in order to reach M1. The book has its Pythagorean triangle mixed up, in regard to the interferometer: c should be the velocity vector moving directly away from the eye and v’ should be the hypotenuse. If the light ray were heading at an angle upstream at velocity c in order to reach M1, as in the book, then we would need a physical explanation for that angle. Why would the central mirror reflect at an acute angle? On the other hand, if the angle is really 90o and there is an ether wind blowing part of the light toward M 2 at c + v, then why isn’t that same wind blowing the M1 light off to the right, making it miss the mirror? The book can explain none of this.
But what of boat 2? Where does the analogy fail there? It fails because the boat is really being carried by the stream; the light is not being carried along by an ether wind. The ether wind is a tenuous concept, only meant to imply that the interferometer is not at rest relative to the coordinate system of the light ray. Notice that when the ether wind and the light ray are “moving” in the same direction, we still subtract them from each other. Finally, the best way to show that the ether wind is not equivalent to the stream is to see the last paragraph above. If you give c + v to the light ray, then you cannot also give v to an ether wind. Either the light ray is going c + v, or the ether wind is blowing v, but not both. If the light ray were going c + v, and the ether wind were blowing v, then the light ray would be reflected from M2 at c + v, the wind would tamp it down by v and we would have the light at c. This is obviously absurd. The interferometer is not analogous to the boats.
The interferometer was misinterpreted not because it was pre-Einstein. Notice that my critique of the interferometer is not an after-the-fact critique, using information from Special Relativity. Special Relativity, according to Einstein’s interpretation, says that the interferometer cannot work because light moves c relative to all measuring systems. It says that light cannot go c + v. But as MM has shown, this is false. In order to arrive at his transforms, Einstein adds v to c several times. MM does the same thing. No, the reason the interferometer doesn’t work is because scientists and mathematicians in the last 150 years haven’t been good at combining geometry and algebra. They have been interested in “higher math,” like the tensor calculus, and few or none have taken the time to learn the subtleties of simple problem analysis, applying basic algebra to spatial and temporal problems. Space and time are not even agreed to exist anymore, in the way that Maxwell and Michelson thought of them. So an analysis like MM has done here is thought to be passé. This is why such stunningly fundamental errors have been let pass for more than a century.
Some have said to me at this point, "If all this is true, it seems to imply that the system of earth+light really can have a velocity greater than c, which is what Michelson was trying to show all along. But this contradicts Einstein." Yes, it does contradict Einstein, in a way. If you take Einstein to mean that one cannot measure a system to be going greater than c, MM would say it does not contradict him. For you cannot directly measure the sytem of earth+light to be going greater than c, even though MM agrees that it must be. It must be, or else we would not be privy to red-shifting or blue shifting. But it cannot be measured because you cannot invent the proper background to see it with. You cannot see yourself moving. You can calculate it, but you cannot see it. You can calculate a local velocity, but you cannot measure something against the background of that velocity. If you are in a car going 60mph, you know you are going that fast, but you do not see yourself as moving. You see the rest of the world moving. This is very important in relativity theory, especially regarding the measurement of c. For, what if you, in the car, now want to measure the velocity of a car going by in the other direction? You say, I can see the movement of that car not only relative to me but also relative to the ground. Alright, but now let us say you have to measure the light you are seeing all this with, relative to you. Not to the ground, but to you. You know that the speed of the light in front of you, which is the light you are seeing, must be c + v. But how could you possibly see it or measure it like that? You see yourself as stopped, relative to yourself. In your co-ordinate system, you are at rest—that is what makes it your co-ordinate system. And you see yourself with the very same light you are trying to measure. You can only see yourself as stopped relative to light. Therefore you can only measure light to go c. You can calculate that you+light is greater than c. This is allowed. If this contradicts Einstein, then so be it. But the interferometer was not a calculation: it was an attempt at measurement. It was the attempt to see light from a non-local field. This is one reason it was absurd. Another reason is, of course, the math proposing to predict a fringe effect.
Some will say, "Well, if the M/M illustration is wrong, simply move the data-collecting scientist off the earth and run the experiment. Then you will get meaningful data.
You won't because you can never get away from the lightray you are measuring. You cannot measure or see a lightray that is not in your co-ordinate system. You cannot make a measurement of light from a distance. You can set up the most elaborate device in the world, but you will still find the ray of light has ended up in your back pocket. At the end of the experiment, in order to collect any data, the light will have to come back to you. In which case it will arrive moving directly toward you. And you will not see it until it impinges on your device, at which time it is part of your co-ordinate system.
You may also be interested to know that Einstein stated that there was no absolute test of simultaneity. He said that no observer could claim preferential status. MM thinks he was wrong in this. Using the Doppler effect, an observer could derive that he was neither red-shifted nor blue-shifted in relation to the incoming data. This observer, unmoving in relation to both events, might easily say that his claim of simultaneity was infinitely more meaningful than anyone else's. The Doppler effect is already used to calculate relative velocities (of Quasars, for instance). It would therefore not be difficult to calculate who was in a position to determine simultaneity, and therefore an absolute simultaneity for given events.
At any rate, M/M expected to find the light rays returning to their central mirror out of phase. That is, one ray was expected to be a little late, causing a fringe effect to be observed by the eye. As MM has shown, this was a false expectation.
As you can see, the entire problem was undermined by a poor conceptualization. This prompted the use of faulty equations to explain it (by Lorentz), which were then borrowed by Einstein to express Relativity.