Unifying the Photon with other Quanta,
How they Travel,
and why they go c
© Miles Mathis Abstract: In Part I of this paper will unify the photon with all the other quantum particles. It will also show the mass of the photon, with simple math. (This mass is below the current standard-model limits set by various experiments.) Part II: How Do Protons Travel Part III: Redefining the Photon and Why it is going c The truth is, it only took a few moments on the calculator to discover that the photon is simply another energy level of the quantum. In the following papers MM has shown that all the particles are just spin levels or multiples of the same particle. : This unification was made easier since in G is the Key to the Secret of Gravity, MM has already applied G to the radius of the photon. MM has shown that the universal gravitational constant in Newton’s equation is actually a scaling constant between the photon and the hydrogen atom or proton. Newton’s equation contains the E/M field, hidden by the un-mechanical variables. G acts as a scaling constant between the gravitational field in the equation and the E/M field in the equation. Which means that the photon is G times smaller than the hydrogen atom. This explains many things, not the least of which is why G seems to vary slightly in experiment: it varies depending on the elements present. G, as a scaling constant, depends on the size of the atoms present: if most of the atoms are bigger than the hydrogen atom, G will have a margin of error. We know that the nucleon at rest is at an energy level 1821 times above the electron at rest. Using a simple quantum equation in The Unification of the Proton and Electron, MM has shown that this is due to three extra spins, x, y, and z. The electron is spinning axially; the proton is spinning axially plus x, y, and z. Now if we want to find the photon using this spin quantum equation, we look for these same spins, but on a smaller scale. They must be the same spins, since we have no other material dimensions. MM is not proposing new directional or material dimensions, understand, but the same spins in the same dimensions, just on a sub-scale. Spins within spins, if you like. We know the photon is stable, and so are the electron and proton. So we look for a level beneath the electron that would provide this stability. How should we do that, intuitively? Well, we see that two stable levels are 1821 apart. So we postulate that other stable levels are also 1821 apart, for the same reason. The electron and proton are not accidentally 1821 apart, they are 1821 apart due to the way the spins stack, in a simple manner, as shown previously. So perhaps the photon is at one of these sublevels beneath the electron. MM has proposed that the photon is G times smaller than the hydrogen atom. Are G and 1821 linked in some way, mathematically? Yes, they are. If we cube 1821, we obtain 6.04 x 109. If we want to go smaller, we use the inverse of that number, which is 1.66 x 10-10. So in seeking the photon, we should look for a mass at that level: a mass 1.66 x 10-10 smaller than the proton mass. That would be a mass of 2.77 x 10-37kg. But first, notice what was just found: That is too close to 1 to be a coincidence, though it is not possible to tell why the number is 2/5 and not 1. It is possible that it is because G is scaling down to the radius of the photon and we are scaling down to the mass of the photon here. We cannot get the radius straight from the mass, 1 to 1. The mass should be proportional to the energy, but the energy is determined by both a and x-spins. The a-spin corresponds to the radius, but the x-spin is twice the a-spin. Even with that correction, we still have a margin of error, though, since that would give us .5, not .4.
Now let us develop the mass of the photon from another direction, and compare that number with the number we found from G and 1821. The energy of a photon is around 10-19 J, which, using the equation E = mc2, gives us a mass equivalence of 1.11 x 10-36 kg. That is within a factor of 4 of the mass we found by the first method, as you see. To make the correction, we just use a slightly less energetic photon. Photons have a range of energies, so this is easy to do. What kind of photon matches our first prediction exactly? A photon with a mass equivalence of 2.77 x 10-37 kg, or an energy of 2.5 x 10-20J, which is a frequency of 3.77 x 1013/s, which is an infrared photon. An infrared photon has a mass equivalence that is 1.66 x 10-10 smaller than the proton mass. Which means the proton is 18213 more massive than the infrared photon. Is this a coincidence? No. For one thing, the infrared photon is the most common photon, being a large part of the emission from the sun as well as majority of molecular motion. Yes, molecules vibrate in the infrared, for the most part. So, we have found a mass of the photon of 2.77 x 10-37kg. In the paper Bohr's Three Mistakes, we learn that the radius of the photon must be G times the proton radius, which gives us 2.74 x 10-24m. Does that tell us anything? Sit down and hold onto your chair before you calculate. Because if we use MM's simple equation from the paper G is the Key to the Secret of Gravity (relating mass and radius to surface acceleration), we get
a = 4mG /r2 = 9.8m/s2 The photon, like the proton, and the Earth, has a local acceleration at its surface of 9.8! (See G at the Quantum Level) MM has shown that the photon is two full levels below the electron and three levels below the proton. The first question begged is, “Why isn’t there a stable particle one level below the electron?” Good question. Why don’t we find a stable particle with a mass 1/1821 that of the electron mass, which would be 5 x 10-34 kg? If that were a photon, it would have an energy of 4.5 x 10-17 J, and a frequency of 6.8 x 1016/s. So the answer is, we do have a stable particle at that mass equivalence: it is just an ultraviolet photon. photon/ultra-violet photon/electron/proton Which means we need a further question: “Why are photons stable over a wide range of energies, while electrons and protons are not?” Well, electrons and protons are stable over a wide range of energies. They gain energy as we accelerate them, and they are stable at all these velocities, as long as they avoid collision. And, like the photons, they show an increase in wavelength as they accelerate. Which brings up the third question begged: if that is true, then how is it that photons can vary their wavelength without changing speed? An electron has to accelerate to show a different wavelength: electrons going the same speed cannot be different “colors.” But photons can. The answer to this question will be shown later, but the short answer is that photons have two wavelengths. The individual photons have a wavelength that is determined by local spins, just as with the electron. These wavelengths are exceedingly short, being multiples of the photon radius. These are the wavelengths that show themselves in photon traps, and that have caused the mysteries of superposition. But the photon also shows another wavelength at the macrolevel: this wavelength is the wavelength that we see and measure in more common optical devices. The stretched wavelengths we see give us a large variation in energy and color, but the local (real) wavelengths vary by only a tiny amount. This tiny amount is insignificant as measured from our level, so it does not affect the relative energy of the photon, which is its speed. Another question: why don’t photons ever go less than c? Electrons and protons never go c, but photons always do. If they are all the same particle, at different energy levels, why the fundamental difference? A very difficult and complex question, one that MM will address more fully elsewhere; but, in short, the larger particles (like baryons) are slowed and destabilized by gravity. They are also slowed by the charge field, which is like a sea of charge photons. Larger particles are bombarded by all smaller particles, and can accelerate only with difficulty. The smaller particles like photons do not have this problem. Their radii are so small they can dodge most of the charge field. They do not feel the drag of the charge field, and their velocity is mostly unimpeded. (Considering that this contradicts the standard model, it is necessary to review the objections that are bound to be made. Let us go to a University of California website that glosses the standard model on this question:* If the rest mass of the photon were non-zero, the theory of quantum electrodynamics would be "in trouble" primarily through loss of gauge invariance, which would make it non-renormalizable; also, charge conservation would no longer be absolutely guaranteed, as it is if photons have zero rest mass....
It is almost certainly impossible to do any experiment that would establish the photon rest mass to be exactly zero. The best we can hope to do is place limits on it. A non-zero rest mass would introduce a small damping factor in the inverse square Coulomb law of electrostatic forces. That means the electrostatic force would be weaker over very large distances.
Likewise, the behavior of static magnetic fields would be modified. An upper limit to the photon mass can be inferred through satellite measurements of planetary magnetic fields. The Charge Composition Explorer spacecraft was used to derive an upper limit of 6 × 10-16 eV with high certainty. This was slightly improved in 1998 by Roderic Lakes in a laboratory experiment that looked for anomalous forces on a Cavendish balance. The new limit is 7 × 10-17 eV. Studies of galactic magnetic fields suggest a much better limit of less than 3 × 10-27 eV, but there is some doubt about the validity of this method.
MM has to laugh at the first sentence here, since "because we want to save our math" is not a physical argument. MM has shown in dozens of papers that QED is in serious trouble, and MM has no concern for the safety or continuance of gauge math or renormalization. Gauge invariance was lost long ago: that is what all the symmetry breaking was about in the 70's, remember? In The Weak force is not a Force but a set of Collisions MM shows that both gauge math and its so-called invariance is a farce. The symmetry is strictly mathematical: it was part of the equations before anyone applied them to reality, so the invariance is all manufactured. Whether we can save it is therefore not a physical or mechanical question. As for renormalization, MM has shown that physicists should be embarrassed to continue that trick: they should be glad to get rid of it. Even Feynman, who invented the largest part of it, said it was hocus-pocus. As for charge conservation, in the paper Why Magnetic Monopoles cannot Exist on his site, MM has shown that there is no such thing, since the charge field isn't even a real dipole. As a question of mechanics, all charge is positive, so there is no way to conserve it. As for these upper limits, MM will first point out that MM's mass is below the first two limits. 7 × 10-17eV is equal to 1.25 × 10-36kg, and MM just found a mass for the photon of 2.77 × 10-37kg. This is not to say that MM accepts any of these limits, or the experiments they come from. The planetary magnetic field number is possibly correct, and MM would have to study the experiments more carefully to criticize it, but the Cavendish number is highly suspect. MM has shown in MM's paper on Cavendish on his site that the experiment has been misunderstood from the beginning, so any tinkering with a modern Cavendish device must be taken with a grain of salt. Finally, even this quote admits that the galactic field number is in doubt, as it should be. We still can't measure distances to galaxies with confidence**, so field measurements must likewise be very imprecise. This limit is meaningless.
But to move on. Another question begged: why is there not a stable particle 1821 times the proton mass, and so on up? This first level above the proton would be a particle with a mass of 3 x 10-24 kg. There would also be a particle at about 3 x 10-11kg and at about .2 kg. The answer to this question is “gravity.” At the mass and size of a proton and below, the variance in energy caused by gravity is a very small part of the total. MM has shown that it is much larger than QED thinks, but it is still small enough that it does not cause instability. According to the standard model, gravity is negligible, being at least 1038 times weaker than E/M. In MM's unified field equations from his paper Newton's law is a Unified Field of Gravity and E/M, gravity is large enough to enter the calculations, even at the size of the atom. When we get 2000 times larger than the atom, it has already begun to cause instability in the spin equations. MM will also have much more to say about this in subsequent papers, but in MM's unified field papers you can already see that gravity must be a measurable fraction of the total field long before we reach the size of visible particles. You can see this very clearly in the math in MM's paper on Cavendish on his site, where MM calculates the relative sizes of the gravity and E/M fields at various levels of size. Now for the toughest question begged: “How can an electron be composed of a photon, with two levels of stacked spins, plus its own axial spin, and then emit photons in order to create the charge field? In this scenario, you have photons emitting themselves!” Good question, and it is made even more difficult if you add this one: “If a photon can dodge the charge wind, made up of other photons, how does it ever get the seven extra spins to become an electron?” This is also difficult enough to merit another paper, but MM will go ahead and use it to finish off this paper. MM will answer the second question first, since it is a bit easier. Once again it is simply a matter of size. Photons do collide all the time, but because they are the same size, they normally don’t cause much slowing. The odds of a direct hit are very small. Indirect hits cause spin, not slowing. So collisions do cause all the spins, without much slowing. Of course direct hits do happen, but these hits do not cause annihilation. They cause temporary stoppage of both photons. Stopped photons are sitting ducks: their odds of direct collision go way up. So they get re-boosted by other photons and eventually reach c again. The small fraction of photons that get stopped simply lowers the average speed of all the photons. This would mean that c is the average speed, not the maximum speed. So it is possible, according to this theory of collision, that newly emitted photons may be going slightly over c for a short time, until they suffer a number of collisions. Electrons and protons and all larger particles feel a photon wind, and this photon wind slows them. Larger particles get spin from each other, but they get slowed mainly by photons. Photons don’t impart spin to larger particles because spin requires a small size differential. A small particle and a large particle can’t often hit “edge to edge”: the odds show us that it is much more likely the small particle will impact away from any edge of the large particle. Just think of taking random shots at a large globe with a BB gun. Almost all the shots that hit it will be absorbed, or will knock it back. The odds of hitting the globe with a BB right on an edge, so that it imparts spin, are very very low. But if two BB’s meet in flight, the opposite is true. The odds of a direct hit are very very low. Spin is the most likely outcome of any hit. This explains some of the main differences between photons and hadrons. Still, how can a photon with seven or eight spins become an electron and start emitting large numbers of photons? The short answer is that it is not emitting them, it is re-emitting them. As the photon gather spins, it stops acting like a simple particle with linear motion and starts acting like a little engine. The spins allow it to trap other photons. Specifically, the z-spin is orthogonal to the linear motion, which allows it to act like a scoop or an intake valve. Photons with only axial spin cannot resist this intake, and they are temporarily absorbed by the photon with z-spin. Intake of small photons begins to slow the large photon and it begins to turn into an electron. It gains mass and loses velocity. At some point it takes its fill of small photons and they start to spill out once more. The large photon has become an engine, driven by small photons. It is now an electron. This photon exhaust of this little engine is what we call charge. If you have enough of this exhaust, it begins to directionalize the residual photon wind, and this photon wind is what we call electricity. The spin of the photon wind is what we call magnetism.
This is the basic mechanism of charge. Of course MM has only outlined a bare bones theory here, and MM has much work to do. But you can see that requiring a strictly mechanical explanation has continued to lead me into fertile fields. For a century it has been thought that mechanics was a necessary limitation or hindrance at the quantum level. It has been thought that the sort of explaining like this is impossible. But it is not impossible. Asking and attempting to answer the sorts of material and kinematic questions and answering here is the only possible way to progress at any level, quantum or cosmic. Addendum, Feb 2012: Some in the mainstream are already moving in the direction of this paper. A reader just sent me to a 1997 paper by Williamson and van der Mark, and they are proposing a similar electron construction to mine. Unfortunately, they have kept a lot of mainstream dogma which MM has shown is incorrect. These quantum problems require an entire array of simultaneous corrections, and they have only spotted some of them. They are also keeping the difficult math and complex wording, to impress their colleagues, which is understandable. If you find MM's papers way too breezy, you may prefer theirs. But if you want a bare bones explanation, MM's quantum spin equation in The Unification of the Proton and Electron is much simpler than their toroidal construction. *http://math.ucr.edu/home/baez/physics/ParticleAndNuclear/photon_mass.html Abstract: MM developes a firm number for the local wavelength of the photon, show how it is created by the spin of the photon, and how this local spin is stretched by the linear motion into the wavelength we see and measure. MM proves that the transform from the local wavelength to the measured wavelength is c2, showing why this term is found in the famous equation E = mc2. In Superposition is not Mystical, MM has shown that photons have a number of stacked spins, but here we will look at the linear motion of photons, showing how the measured wavelength is caused by the wavelength of the spins, and how different colors are created. Before we get into that, MM would like to give credit to Descartes, who knew that color was caused by photon spins in the early 1600's. MM believes he made this proposal in Dioptrique, around 1638. This was before Newton's corpuscles, so the fact that Descartes was able to intuit an answer so close to correct at that time is extremely laudable. If MM has remembered correctly, Descartes got the energies reversed from red to blue, but connecting color to spin was a masterstroke in itself. We will see that color is due to the size of the photon, which is more a matter of radius than spin velocity, but the two are inextricably linked. It is spin collisions that cause the spin radius, so we would obviously have no spin radius without spin. Since in MM's paper on his site Why Does a Rainbow
Curve Down he recently published strong evidence against Descartes' theory of reflection by the back surface of raindrops to create rainbows, he felt compelled to add this paragraph to this paper, showing he was also often right against very long odds. From G is the Key to the Secret of Gravity, we know that the radius of the B-photon is G times less than the radius of the proton. This gives us a photon radius of 2.74 x 10-24m. The z-spin is 8 times the radius, so we should find a basic wavelength of 2.2 x 10-23m. Obviously, we don’t find photons with a wavelength that small. Why? Simply because the wavelength we measure has been stretched out by the velocity of the photon. The photon would be measured to have a wavelength of 2.2 x 10-23m only if it were at rest. You will say, “Even if we accept that the photon is spinning, how can the z-spin be stretched? The spin would give us a spin radius, which is just a length. A length cannot be stretched by motion, unless you are proposing some kind of relativity here.” MM is not proposing relativity as the solution here. The answer to your question is that a spin is not just a radius, and is not just a length. A spin is a motion: a motion that takes time. Even if the photon were spinning at velocity c, one rotation must take some real time. We know that the linear velocity of light is not infinite, so we must assume the speed of spin is also not infinite. If it is not infinite, it must take time. If it takes time, then it will be stretched by the linear motion. While the surface of the photon is spinning, the photon as a whole is moving some linear distance x. So how much does the velocity stretch out the wavelength? We can discover that most easily by using this simple equation:
E = mc2 = hc/λ Let us take an infrared photon, as our first candidate. The mass equivalence of the infrared photon is 2.77 x 10-37 kg, so we just solve:
λ = h/mc = 8 x 10-6m If we compare that to the wavelength at rest, we find the wavelength has been stretched out by a factor of about 3.63 x 1017. Since that is very nearly c2, we assume that the transform is in fact c2, and that the difference is a difference between the size of the B-photon and of the infrared photon. Remember that we developed the at-rest wavelength from the B-photon and the moving wavelength from the infrared photon. Our assumption is borne out by the numbers, since if we divide 8x 10-6 m by c2, we get 8.9 x 10-23 m, which is almost exactly 4 times our B-photon wavelength. We may assume that the infrared photon is about 4 times larger than our B-photon. But why c2? Let’s look at the mechanics, to find out. As usual, nothing esoteric is going on here, so we can analyze just as if we were analyzing pool balls. If the photon is spinning while it is going c, and the radius is being stretched by a factor of c2, then that must mean that the photon is spinning at a velocity of 1/c. It takes one full rotation to create a single wave, since the rotation is physically creating the wave. And we want to find one full rotation while the photon is moving 8 x 10-6m. That will give us the wave we measure. At speed c, the photon goes that far in 2.67 x 10-14 seconds. So the photon has spun once in that time. By MM's new kinematic circular motion equations in "π (pi) is 4 not 3.14....", the circumference is 4 times the diameter, so a point on the surface of the photon travels 8.8 x 10-23 m. If we divide the circumference by the time, we get 1/c. Which begs another question: Why would the spin be the inverse of the linear velocity? Because both are dependent upon the same fundamental factor: size. The smaller the quantum is, the faster it goes. The photon goes c precisely because it is so small. It can maximize its speed because it can dodge most other quantum traffic. But this size also determines its spin rate. Notice that we have found it to be spinning extremely fast: 1 cycle every 2.67 x 10-14 seconds, which is equivalent to 3.7 x 1013 cycles each second. That is extremely fast, from our point of view. But, as MM has just shown, from the photon’s point of view the surface is moving incredibly slowly: 3 x 10-9 m/s. That is because one cycle is such a tiny distance. With such a tiny circumference, the photon can move with a tangential velocity of 1/c, and still achieve an astonishing local frequency. That being true, it still doesn’t provide a mechanical link between c and 1/c. MM has shown that the photon can move very slowly, in its own realm, and still create the necessary wavelengths and frequencies we see, but “very slowly” and 1/c are two different things. Why 1/c, precisely? Because, as we know, velocity is a relative measurement, and we are measuring the spin velocity relative to the linear velocity. MM will show this with a diagram: Here we have only the linear velocity and the tangential velocity. MM has drawn the linear velocity only a bit larger than the tangential velocity, but let us say we are given a tangential velocity of some magnitude x. We let that magnitude remain constant and we begin increasing the linear velocity. So one line gets very much longer than the other. Obviously, if we make one line very much longer, we no longer need be concerned about the real magnitude of x. We only care about its magnitude relative to the linear velocity. As the linear velocity approaches infinity, the relative tangential velocity would approach zero. This is sometimes called the math of very large numbers, and it allows us to dispense with absolute values. Since velocity is not an absolute value to begin with, this is very easy to do. You may say that c is not really a “very large number”, but relative to the radius of the photon, it is. We have 31 orders of magnitude between the two, which is a very large number by anyone’s reckoning. So, as the linear velocity gets larger, the tangential velocity gets smaller relative to it. And the difference between the two is so large that the relationship becomes nearly a perfect inverse relationship. In other words, c2 is so large that the tangential velocity can be estimated very successfully with just the transform 1/c. This also happens to be the reason we can ditch the ½ in the equation E=mc2. The two equations E=mc2 and E=½mv2 are supposed to be analogous, at least when the first one is applied to a photon and the second one is applied to an electron, say. Nearly all the energy of a photon is kinetic energy, so the equation E=mc2 applied to a photon is an expression of kinetic energy, with m as the mass equivalence of the photon. But the equation has no ½. The reason it doesn’t is that because c2 is so large, ½ becomes negligible. One half of almost nothing is still almost nothing, so we can ignore it as a factor. This is explained in more detail in the paper Why does the Kinetic Energy Equation
have a squared Velocity. ω = √[2r√ v2 + r2) - 2r2] If we insert our numbers for the photon into this equation, using v=c, we get ω≈√(2rv) = 4 x 10-8m/s. That is close to 1/c, so we see that it is not the tangential velocity that is 1/c, it is the orbital velocity of the photon that is 1/c. If we let the tangential velocity of the spin of the photon equal c, then the orbital velocity is 1/c. That is due to this equation, and the fact that the value of r is so small. And this has other major consequences. It means that Einstein's famous equation must be clarified as well. It now reads E=mc2. But MM has just shown that the two variable assignments of c in that equation are not equivalent. So, although the equation stands, we must subtly rewrite it. One of the c's is the linear velocity of the particle and one of the c's is the tangential velocity of the spin. This makes the expanded equation E=mcLcT Since both values of c are the same, the equation does not change in number outcome, but we now have a much better understanding of what the equation stands for, and what mechanics it is representing. We are squaring c to represent both the linear energy and the spin energy of the particle. The orbital velocity of the particle is 1/c, and this allows us to see how the wavelength is stretched by the linear motion. But when we want to calculate the total energy of the particle, we have to combine the linear velocity with the tangential velocity. This is because the two velocities are straight-line vectors and can be multiplied without a transform. As MM has just shown, when the tangential velocity is c, the orbital velocity is about 1/c. Some will say that MM is assuming a longitudinal wave for light, whereas Fresnel proved that light has a transverse wave. If MM is able to multiply MM's local spin wavelength by c2 to get a visible wavelength, MM's local wave must be longitudinal. But that is not correct. Since the wave of light belongs to each photon, via spin, the wave is neither longitudinal nor transverse. Longitudinal and transverse waves are defined as field waves, and light is not a field wave. Light is a spin wave, and the spin is neither transverse nor longitudinal. The local wavelength is just a radius of spin. However, since MM has shown (in MM's paper on superposition) that any electromagnetic radiation must have at least two stacked spins to show a physical wave, this stacking can mimic either transverse or longitudinal waves, depending on the experiment and the effect studied. Fresnel was studying polarization, and although Young had already shown both longitudinal characteristics and transverse characteristics, the polarization experiments seemed to confirm only the transverse part of this duality. And, indeed, polarization can be explained with only the transverse characteristics of the stacked wave. Other experiments and effects are better explained as the stacked spins mimicking longitudinal waves. This is what is happening with Tesla or plasma waves which are longitudinal. In plasmas, the spins beneath the outer spin come into play, and the axial spin of the moving electron is no longer hidden. The charge field coheres or links these inner spins, creating uncommon effects. At any rate, wave theory will not advance beyond its current wall unless it comes to see that both transverse and longitudinal waves are a misconception, built upon a mistaken field wave theory that is an analogue of fluid or sound dynamics. Light waves are not field waves, they are spin waves. Light is its own field, since light is both the linear motion and the spin motion of the photon. So, MM has explained the motion of the photon in a simple manner, providing us with not only a spin but a rate of spin. MM has developed actual numbers, first the radius in G is the Key to the Secret of Gravity and second the mass of the photon in the first part of this paper, and now for the rate of spin and the tangential velocity and orbital velocity. MM has shown how this spin rate creates the visible or measurable wavelength of light. The radius of the photon’s spin creates the actual wavelength, and then this length is stretched out by the linear motion, giving us the measured wavelength of the light. But now we must move on to ask why and how photons express different wavelengths. Electromagnetic radiation, in the form of photons, comes in a wide range of wavelengths, as we know. How is this achieved? It is achieved by a wide variation of stacked spins. At the beginning of this paper, MM showed that it turns out that photons can maintain a linear velocity very near c over a wide range of sizes. The photon does not reach a size limit that causes slowing until it approaches the spin radius just beneath the electron. At that limit, the largest photons begin absorbing the smallest photons, and the mass increase snowballs. This turns the nearly massless photon into the small-mass electron. The most common photons appear at the size range of 18213 less than the proton mass and size. This is where we find the infrared photons, as previously shown. But the small mass of the photon allows it to stack spins over a wide range of radii. In this, it is unlike the electron or proton. The proton cannot add extra spins above the z-spin without creating instability. This is why “mesons” over the baryon size are not stable. (See Mesons without Quarks.)
The extra spins begin interfering with the energy of the inner spins. But with the photon this appears not to be the case. Extra spin levels do not cause appreciable slowing, nor do they cause appreciable instability. We may theorize that smaller photons would be more stable, but the difference in small photons and large ones is not easily measured from our level. What this means, specifically, is that if we give the infrared photon a z-spin as its outer spin, we can find a smaller photon whose outer spin is the y-spin. We can also find a larger photon with another axial or x-spin on top of the infrared’s z-spin. In this way, we find not only stacked spins, we find stacked levels. In other words, we find spins of a1, x1, y1, z1 and a2, x2, y2, z2 and a3, x3, y3, z3 and so on. By this analysis, a2 has twice the spin radius of z1. In fact, each spin has twice the radius of the spin under it. This means that photons do not come in a continuous spectrum. No, they come in stepped levels, each level double the one under it. For example, we found a wavelength of 8 x 10-6 m for our infrared photon. You will remember that number comes from (c2) 8.8 x 10-23 m. If we want the next photon larger than that, we double the spin radius to 1.76 x 10-22 m and multiply by c2, which gives us 1.6 x 10-5 m. There can’t be any wavelength between 8 x 10-6 m and 1.6 x 10-5 m. If we measure light with an average wavelength in between those numbers, we must have a mixture of photons. A single photon cannot be found with a wavelength that is in between those numbers. It must have one wavelength or the other. This explains many optical effects, including rainbows. Rainbows do not have a continuous spectrum, and neither do prisms. We see bands of certain colors. Photons only come in certain colors, and they do not come in the colors in between. In between colors have to be created by mixing photons. It is known that light is quantized, but no one before me has proposed an explanation of this sort for it. Photons have always been considered point particles, with no radius and no mass. For this reason, it was thought that spin could not be a possible cause of quantization. Therefore we have gotten many complex mathematical explanations of quantization, with no mechanical explanation at all. MM has just shown you the simple mechanical cause of quantization. Addendum: many have asked why these charge photons have not been discovered. MM's answer is that they have. All the photons we already know about are part of the charge field. The entire electromagnetic spectrum is the charge field. We do not have to propose new photons, we can use the ones we already have. MM has given all photons mass and radius, so all photons must cause mechanical forces by contact. This has long been known (see the photo-electric effect) but not fully interpreted. Now that MM has some new equations for the photon, previous papers can be updated
with this new information. This paper will be a sort of compilation of all MM has shown about the photon to date. Previously above , we found
Eγ = 2rγ√c = mγc2 MM has shown that we can find the mass of the charge photon by using the same scaler as we use
between the electron and nucleon. That scaler MM has called the Dalton, and it is the number 1821. But
since the charge photon is two levels below the electron, we have to square it:
mγ = me/(1820.56)2 = 2.75 x 10-37 kg
Which gives us
By energy, this makes the charge photon infrared. By wavelength, it makes the charge photon
ultraviolet. But since MM has thrown out the current wavelengths as inapplicable to the photon itself, we
should look at energy. The charge photon is still infrared.
When MM said we would have to reverse the charts, he didn't mean we would switch infrared with
ultraviolet, or something like that. MM meant that to keep the energies the same, and keep the chart as-is
in that way, we would have to reverse wavelength and frequency. Now you see what MM means by
reversing the wavelength. What was infrared remains infrared, since we continue to label light by
energy. But infrared photons now have smaller wavelengths than ultraviolet.
As for frequency, MM doesn't talk about it when labelling photons, because it is no longer a direct function
of energy. The energy of a photon isn't determined mainly by its spin frequency; it is determined by
how many stacked spins it has. Higher energy photons have more stacked spins.
As to the question why light is going c, the information is
contained in the equations above. We start with this equation:
mγ = 2rγ/c√c
That means that the velocity c is a function of the photon's mass and radius. In other words, its speed
is determined by its size in the field, just as we would expect. In the macro-world, we would need one
other variable to solve, that being the density of the charge field as a whole. MM has recently found the
mass equivalence of the charge field relative to the matter field (baryonic matter), that being 19 times.
This is where we are getting the “dark matter” number of 95%. But that doesn't give us a universal
charge density. In fact, according to MM's theory and equations, there should be no universal charge
density. Charge should be denser in galaxies than out of them, and denser near stars, and so on. By
this analysis, it seems that the velocity of the photon would change in different densities. Because this
appears not to be so, MM assumes that the mass of the photon may change depending on the charge density
around it. Remember that mass is a function of energy according to the old equation Eγ = mγc2, which
means that the photon's mass is already a function of the charge density. As the charge density grows,
so will m. So that variable m already includes the charge density, in a way. This feedback mechanism
may be what keeps c constant.
The charge density is determined by the size of the photon and the size of the charge field. We don't
have to include mass in a determination of field density, since we can calculate the density of empty
boxes in a given size room, for example. Fifty boxes per room, say, or a hundred boxes per room. It is
like a population density in a country. You don't need to know how much each person weighs, do you?
But if you want to know how crowded the country is, you do need to know the size of each person.
That is the sort of density MM is trying to find here:
D = 3√(2rγ)n/V
That's the equation for population density of the charge field. We don't use a spherical size for the
photon. We have to square it out, because not all space is usable. In other words, in a population
density, a sphere takes up just as much space as an equivalent cube.
But we can also write the volume V in terms of the radius of the photon. Since we have cubed out our
photon, the volume is just some number N times the radius of the photon. That is how many photons
would fit in the volume at capacity.
V = 3√(2rγ)N
Now, we can also calculate the density due to mass, by the old equation D = m/V. It won't be the same
number for the density, but that won't matter, because we are now representing the population density
by n/N.
Nm = DV
That represents c as a function of the radius of the photon and the charge density.
D3 = rγ2/√c9
That seems about right, since it would be about 56 million photons per cubic meter.
If we divide that into the proton mass, we get 108. Why is that important? Because it gives us another
way of calculating the energy increase of the proton in an accelerator. It has been found experimentally
that the proton has a mass increase limit of 108m. MM has already found one way of calculating that
limit, using the gravity vector of the proton and the Relativity transforms. However, this method is
more efficient, as you see. And this method shows it is the charge field itself that is preventing the
proton from going any faster. The proton is simply too big to move any faster in the field. The only
way it can accelerate past 108m is to shed its outer spin and become a meson. Many have asked why we haven't discovered the charge field and especially since MM claims it is ubiquitous. The reason for this is that the answer is hiding in plain sight. To begin with, the The Hubble Redshift is just curvature is proof of MM's charge field, since that is what the CBR is. MM has shown that the CBR is not a residue of the Big Bang, it is simply the average or ambient charge field of the universe. Beyond that, the entire electromagnetic spectrum—the one we already know about— acts as the charge field. We do not need to propose any new dark photons to act as the charge field; nor do we need to create experiments to find them. Since MM has shown that all photons have mass and diameter, all photons are capable of transmitting forces by contact. This has long been known, in part. See, for example, the photo-electric effect. We have known for over a century that photons were capable of knocking electrons out of various materials. If photons can do that, then they are already creating straight mechanical forces of bombardment with forces by contact, so any photon can act as a charge photon. In fact, ALL photons act as charge photons. Some photons may act in ways that transcend their simple charge function, as when they have the correct energy to cause other phenomena, but MM proposes that all photons act at a fundamental level as charge photons. They fill this function simply by hitting other matter, and by spinning.
In this model, G becomes a scaling constant to the average size of the charge field, but every photon in the charge field does not need to have a size or energy defined strictly by G. This would also explain the small variance in G. MM has already explained the small variance in G by the variance in the average size of atoms present, but it may also be caused by the variance in the average size or energy of the photons present. MM proposes that an experiment with ultraviolet light and hydrogen would produce a different G than an experiment with infrared light and lead. MM has shown that the charge field
peaks in the infrared, with an average energy around 10-7m. As above using G as the scaler between
proton and photon size, the radius of the photon was found to be 2.74 x 10-24m. If we multiply that by c2 In closing, MM would like to return to the polywater controversy for a moment. Polywater was discovered by Nikolai Fedyakin in the late 1960's. It was just water forced
through narrow capillary tubes, as in a plant. It showed some structured characteristics, including
increased viscosity. Richard Feynman discredited it, saying that polywater was an idea that disproved itself, since if it existed, there
should be an animal that could live by taking in water and excreting polywater. This just proves that
once again Feynman didn't understand the charge field. To start with, he has it upside down. The
animal would have to take in polywater and excrete water. Polywater is both more ordered and more
energetic. Therefore if the animal wished to excrete negative entropy or disorder—as the mainstream
tells us living organisms do—it would have to excrete water. Beyond that, if we only look at energy
levels, polywater must have more energy. It is channeling more charge more efficiently, therefore the
animal would want to take in polywater, given the choice. And, in fact, Feynman's “animal” does exist. It is called a plant. Plant's don't exist only on this eating
and excreting, but it is one of the things they do. They use narrow tubes to create polywater from the
charge field, then excrete water through transpiration. In this way they feed almost directly on the
charge field in this process. As a side effect, the charged water helps them transport other molecules,
which they also use to live. All plants and animals ultimately feed on the charge, either directly or indirectly. Every entity above
the size of an electron feeds on the charge field, including protons, planets, and galaxies. If Feynman
had understood physics to the extent he thought he did, he would have known that.
Please note that this paper is a simplification by me of a paper or papers written and copyrighted by Miles Mathis on his site. MM has replaced "I" and "my" with "MM" to show that he is talking. All links within the papers, not yet simplified, are linked directly to the Miles Mathis site and will appear in another tab. (It will be clear which of these are Miles Mathis originals because they will be still contain "I" and "my".) The original papers on his site are the ultimate and correct source. All contributions to his papers and ordering of his books should be made on his site.
(This paper incorporates Miles Mathis' photon paper, photon2 paper, photon4 paper, photon3 paper and a section of review of Gerald Pollack's book The Fourth Phase of Water.)
The Unification of the Proton and Electron,
A Reworking of Quantum Chromodynamics unifying proton, anti-proton, neutron, all the neutrinos, and
Mesons without Quarks
Notice that quantum is singular since MM has shown that all quanta are aspects of one quantum.
(G)18213 = .4
**http://www.universetoday.com/2006/08/07/the-universe-could-be-larger-than-previously-thought/
Part II - How Do Photons Travel?
λ = h/mc
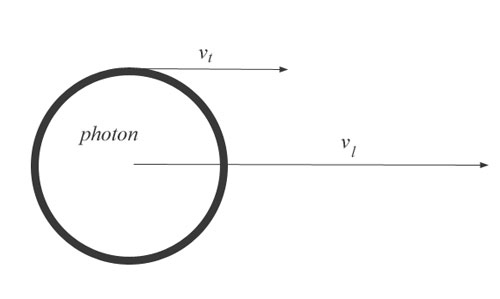
To clarify even further, MM will show the math for this. All MM has to do is import MM's new equation which takes us from v to ω. MM developed this equation by correcting Newton's orbital equation a=v2/r. Current physics believes that the tangential velocity and the orbital velocity are equal, but they are not. Newton assigns them to different vectors or arcs, and then attempts to show they are equal at the limit. In A Correction to Newton's Equation a=v2/r, MM has shown that Newton's math fails. In MM's new equations, ω is the angular velocity measured in meters/s, not radians/s, and we can go from v to ω with a simple equation. MM used this equation in his paper Bohr's Three Mistakes to show the real radius of the electron, and to correct the Bohr radius.
Part III - Redefining the Photon and Why they go c
mγ = 2rγ/c√c
r = mc√c/2
λ = 8E(rγ/mγ) = E(Cγ/mγ) C is circumference of the photon (z-spin)
mγ = E(Cγ/λ)
λ = Cc2
E = λ/4c√c
Eγ = 2.47 x 10-20J
rγ = 7.13 x 10-25m
λ = 5.13 x 10-7m
Cγ = 5.7 x 10-24m
c = 2rγ/√c)mγ
c3 = 4rγ2/mγ2
c = 3√(4rγ2/mγ2)
3√2rγ= DV/n
D = n/N
m = DV/N = 3√(2rγ)D
m6 = 4D6rγ2
c3 = 4rγ2/mγ2
m6 = 4rγ6/c9
4rγ6/c9 = 4D6rγ2
c9 = rγ4/D6
But let's solve that equation for D, to see what the average density of the charge field is:
D = 1.54 x 10-29 kg/m3
Where are the B-photons?
Excepts from Review of Gerald Pollack's book The Fourth Phase of Water
(2.74 x 10-24m * 8.98755 x 1016 m/s = 2.46.2 x 10-8=246nm), we
get 24.62 2.5 x 10-7m or 250nm. That is the wavelength we measure.
The wavelengths of visible light are:
From Wikipedia:
Violet: 380–450 nm (688–789 THz frequency)
Blue: 450–495 nm
Green: 495–570 nm
Yellow: 570–590 nm
Orange: 590–620 nm
Red: 620–750 nm (400–484 THz frequency)