Miles Mathis: Coulomb's equation is a Unified Field equation in disguise

Please note that this paper is a simplification by me of a paper or papers written and copyrighted by Miles Mathis on his site. I have replaced "I" and "my" with "MM" to show that he is talking. All links within the papers, not yet simplified, are linked directly to the Miles Mathis site and will appear in another tab. (It will be clear which of these are Miles Mathis originals because they will be still contain "I" and "my".) The original papers on his site are the ultimate and correct source. All contributions to his papers and ordering of his books should be made on his site.
(This paper incorporates Miles Mathis' charge paper and coul paper and charge2 paper and charge pdf: Vienna State Opera House 2021 How MM discovered charge

Coulomb Faraday

MM will show how Coulomb's equations can be related to Newton's. Also to show that Coulomb's constant is connected to the Bohr radius, mathematically and mechanically. MM will also show that the current constant, though highly suggestive, is incorrect.

Background

Both Coulomb's experiment and Coulomb's equation have suffered various kinds of attack over the years, but MM's analysis here will be of a different sort than any other you are likely to have seen. MM would agree that Coulomb's experiment has been oversold historically and presently, but that question, though perhaps interesting in its own right as a question of the politics of science, is not the central question. The central question is one of fact: is the equation correct in math and theory. MM will show that it is not.

One crucial thing that is always ignored is the fact that Coulomb's spheres are spheres. The experiment and equation could not work if they were not, but we are never told this. It is always a matter of charge, never of shape. But the reason we get an inverse square law is due to the spherical shape of Coulomb's objects. Because they are spheres, they must emit a spherical field, and a spherical field must obey the inverse square law.

Current theory ignores this in a most flagrant manner, and they do so because they must ignore that the charge field is an emitted field. The field stops being mysterious once we realize that the density of spherical emission must fall off with the inverse square, but current theory cannot follow this reasoning. Physicists would rather cloak the field in mystery than admit that it acts precisely like a field of emission. If it is an emission field, they have to consider its mechanics. If they consider its mechanics, they have to quit talking about virtual photons or messenger photons and start talking about real photons with real energy. And if they do that, they have to ask how quanta emit quanta without dissolving. It becomes a fundamental question of conservation of energy.

The reason current theory has to block this line of questioning right out of the gates is that QED and QCD have no answers for it. No only that, but the math they have offered us denies that the field is an emission field. To put it baldly, if the E/M field were shown to be a real field with real energy and mass equivalence, all of QED and QCD would fall into a heap. Faraday assumed the “field” was non-physical and non-mechanical in the 1830's and QED still assumes this.

This is why the E/M field has been cloaked in strange units, constants, permittivities, and permeabilities. At the level of QED, the math does the cloaking without the need of more obvious blankets, but once we get down to the level of classical electrical theory (the kind taught in high school and undergraduate levels) there is a great need for these more ham-handed misdirections. Physicists can't really import Hamiltonians and tensors and gauge fields and complex operators at this level, so they load down the explanations with jargon instead. Instead of drowning you in mathematical jargon, they drown you in verbal jargon: complex terminology and undefined terms.

Here is included Miles Mathis's paper on electricity from charge.html. First posted December 26, 2006
Abstract: MM will show that charge is dimensionally the same as mass. Then MM will show that charge is the mass of the charge photons. MM will also show that the permittivity of free space is a misdefined constant that has nothing to do with free space. The value of that constant is actually the value of the gravitational field of the proton.

Background on Electricity

Let us look freshly at the electrical field, as if we are encountering it for the first time—as if we are aliens just arriving upon earth, uploading books from the Library of Congress and studying them for signs of intelligence. One of the first books ( General Physics, Douglas C. Giancoli, p. 435) we open tells us this,

The conceptual difficulties [of action at a distance] can be overcome with the idea of the field, developed by the British scientist Michael Faraday. It must be emphasized, however, that a field is not a kind of matter. It is, rather, a concept*—and a very useful one.

Let us also look at the footnote referred to here:
*Whether the electric field is "real" and really exists, is a philosophical, even metaphysical, question. In physics it is a very useful idea, in fact a great invention of the human mind.

As honest aliens, we must see that this footnote is absolutely false. The question of how the electrical field works is not a metaphysical one, it is a mechanical one. What Mr. Faraday has done is create a heuristic device that also works as a mental misdirection. Look at what the book says, The electric field at the location of the second charge is considered to interact directly with this charge to produce the force.

So the field was created in order to allow them to say that. Mr. Faraday, desiring to clear up action at a distance, drew a line with a pencil from one charge to the other, called that a field line, gave it no physical reality and no mechanical definition, and claimed that the pencil line interacted directly with the second charge. That is supposed to be a great invention of the human mind. As aliens, we must wonder what would be considered a dishonest creation of a human mind.

The book buries this bit of dishonesty with its own, calling mechanics "metaphysics." This is to warn off anyone from asking the questions we are asking here. Humans do not like to be called names, and these physicists are warning readers that if they ask any questions about the reality of the field, they will be called mean and scary names. Physicists do not like to be called philosophers or metaphysicians, and just the threat of it is enough to move them on. This despite the fact that the question involved is clearly and unambiguously one of mechanics. If transmitting a force from one object to another is not mechanics, nothing is.

Next we notice that the basic unit of electrical charge is either the Coulomb or, less often, the statcoulomb. The Coulomb is defined as an Ampere-second, and an Ampere is defined as “that current flowing in each of two long parallel conductors 1m apart, which results in a force of exactly 2 x 10^-7 N/m of length of conductor.” We also are told that two point charges of 1C will feel a force of 9 x 10⁹ N at a separation of 1m. A statcoulomb is “that charge on each of two objects that gives rise to a force of 1 dyne at the separation of 1cm.”
1 statC = 0.1 Am/c ≈ 3.33564× 10^-10 C

As aliens, our first question would be to ask what physical parameters the Ampere has, in terms of length and time. The books do not seem to want to tell us that. We are only told that the Ampere is used as a defining unit in order to obtain an "operational definition." This means that it is much easier to measure current than to measure charge, so the earthlings have decided to base their units on current. But if we are persistent, we can discover electrical charge in terms of length and time. We have to go to the pages on the statcoulomb, and look at its historical derivation.

There we find Coulomb's law and the calculation of the constant in it.

F = kq₁q₂/r²
k = 1/4π ε₀
ε₀ = 1/c²μ₀
μ₀ = 4π×10^-7 N/A².

Wow, these earthlings really don't want to tell us what they are doing. Here we have three different constants stacked on each other, each with a more obscure name than the last (electrostatic constant, permittivity of free space, permeability of vacuum) and the final constant circles back and is defined in terms of the Newton and the Ampere. We are being led on some sort of wild goose chase.

But we can still squeeze it out of them. Using Coulomb's law and working back from the last constant, we discover that q actually has no dimensions. All the necessary dimensions are given to the constants, and q is just a floater. If a Coulomb is an Ampere-second, then an Ampere must be a Coulomb per second. Go into the last constant equation, concerning the permeability, and substitute “nothing/second” for an Ampere. If you do that, you get the perfect dimensions for the force in Coulomb's equation. This means that electrical charge is mechanically undefined in the SI system. It cannot even be a wave, since a wave must be defined in cycles per second. We don't have any cycles here or seconds. An Ampere is a nothing per second, but a Coulomb is just a nothing.

The cgs system ditches the constant and gives the statcoulomb the dimensions M^1/2 L^3/2 T^-1. This gives the total charge of two particles the cgs dimension gm³/s². This begins to tell us something, since, being aliens, we have a very long memory. We remember that Maxwell gave mass the dimensions L³ T^-2 (see MM's paper G is the Key to the Secret of Gravity) which would make the total charge M². This would give the total charge of two particles the cgs dimension g² or m⁶/s⁴. And this means that charge is mechanically and mathematically equivalent to mass. Coulomb's equation is then not just similar to Newton's equation, it is exactly the same. We could actually write the charges as masses and nothing would change.

If we express one charge in terms of mass and one charge in terms of length and time, then Coulomb's equation gives us the force in gm/s².

q₁q₂/r² = F
(g)(m³/s²)/m² = gm/s²
But we could also express both charges is terms of mass
(g)(g)/m² = F
F = g²/m²
Or in terms of length and time
F = m⁴/s⁴ = v⁴

Notice that this last equation tells us that a force is a velocity squared squared. That is perfectly logical, although it is not something we ever find in these physics textbooks. Wikipedia, under the heading "statcoulomb", will not tell us that charge is the same as mass. Not only will it not admit that charge is dimensionally the same as mass, it goes out of its way to hide it. In this, Wiki is like all other standard textbooks, online and off. It says, "Performing dimensional analysis on Coulomb's law, the dimension of electrical charge in cgs must be [mass]^1/2 [length]^3/2 [time]^-1". But, as MM just showed, that dimensional analysis stops short of completion, by one very important step. Wikipedia asks the question, tells you the answer, but tells you the wrong answer, on purpose.

Now, we must move ahead and ask why the Standard Model spends so much time larking about with permittivity constants and so forth. This is also misdirection. Many people will see those constants and think that free space or the vacuum actually have permeability or permittivity. But the truth is these constants are just folderol. Space and the vacuum only take on characteristics when you fail to give characteristics to your primary qualities. Charge, like mass or length, is a primary quality. It is a quality you assign directly to matter to explain the interactions you see or measure. If you create a quality and then fail to assign it any dimensions, then its dimensions will revert to the vacuum; but not otherwise.

But it is just stupid to create a quality like charge and then refuse to let it have dimensions. Why would any scientist create a fundamental quality, refuse to define it mechanically, and then allow its parameters to be soaked up by the vacuum? A vacuum is supposed to have no parameters and no qualities, by definition. If we are going to give the vacuum qualities, we might as well flip our terminology and start calling the vacuum matter and matter the vacuum. Matter is supposed to be something and the vacuum is supposed to be nothing. But it is now the fashion for both the Standard Model and new theories to assign characteristics to the vacuum instead of to matter. This is nothing short of perverse.

As you can see, it is the old statcoulomb that has a degree of transparency. The Coulomb is defined in the most roundabout way, and then a bunch of meaningless constants are piled on top of it, to obscure it. Why? Why are physics textbooks such a mess? And why are they so much worse now than they were a hundred years ago? Why has the statcoulomb been replaced by the Coulomb? Why have the explanations become more obscure rather than less? Why would physics choose to replace the statcoulomb with the Coulomb, and hide the definition of charge beneath such embarrassing piles of absolute garbage?

Let me show you some more misdirection. Wouldn't it have been more logical to explain the electrical field in the same general terms as the gravitational field? In both cases we have a basic force between two particles. In both cases we create a field to help explain it. Why then vary the logic when expressing these two fields in scientific language? Why choose to express the gravitational field in terms of mass and acceleration, and the electrical field in terms of charge?

Given two large bodies, we see an apparent attraction and we assign the cause to mass. Given two very small bodies, we see a repulsion and we assign the cause to charge. Why not assign it to mass? Or, to put it another way, with large objects we immediately assign the cause of the attraction to the matter involved. The matter either acts directly or creates the field, therefore we call the causation “mass.” Why not do the same thing with small particles? Why avoid mass and matter so persistently? Why create this nebulous thing called charge and never allow it, decade after decade, to be explained mechanically?

With gravity, we assign the term directly to the force. Gravity creates the force or is the force. Mathematically, gravity is an acceleration caused by the force.
g = F/m = N/kg

But the electrical field is expressed without mentioning either mass or acceleration. Instead we have a characteristic called charge, which is either equivalent in dimension to mass (in the case of the statcoulomb) or which has no dimensions (in the case of the Coulomb). Let us skip the Coulomb as a mechanical non-entity and focus again on the statcoulomb. Remember that the statcoulomb is defined as a force at a distance. Well, gravity is also a force at a distance. Or, a statcoulomb is that thing that causes a force at a distance. The charge is not the force or the distance. It is the cause of the force, and the distance just gives us the magnitude.

Again, the same can be said for gravity. With gravity, mass is not the force or the distance, it is the cause of the force, and the distance just gives us the magnitude of the acceleration.
m = F/g = N/a = N/m/s² = Ns²/m = (Ns/m)(s)

You may ask, why did MM goes on to express mass like that? Well, watch this. The Ampere is also defined as 2 x 10^-7 N/m. A Coulomb is an Ampere-second. Therefore a Coulomb is
1C = 2 x 10^-7 Ns/m

So mass may be thought of a Coulomb-second.

The problem with all this is that using current definitions, a Coulomb has no dimensions or the dimensions of mass/second. But a statcoulomb has the dimensions of mass.
statC = L³/T²
C = L³/T³

Can both be right? It is clear that we need to forget about current and finally define the charge mechanically. We must know what physical interactions are causing the forces, in order to clean up this mess.

To do this, the first thing we may notice is that when speaking of the gravitational field, a force does not have to include the distance at which it is felt. A Newton at a distance of 1 meter is the same as a Newton at a distance of 10m. A Newton is a Newton. Admitting this, why do we have as part of the definition of a Coulomb that it is a force at a certain distance?

The reason, of course, is that the electrical force is caused by a large number of subparticles and (according to MM's theory) the gravitational force is not. If we assume that a static repulsion is caused by the bombardment by a huge number of tiny particles, then the total force is a summation of the individual forces of those particles. To obtain this summation, we must know a particle density.

And that is why we need to know a distance and a speed, in order to calculate a charge using the present theory. The distance gives us an x-separation between the two objects in repulsion, and since we assume the density is constant or near constant, the y and z density must be the same as the x-density. This gives us the size of the “field” that is creating the force. The speed gives us the density of the field at a given dt. In this way, the electrical field acts as a third particle moving from one object to the other, imparting the force by direct contact. But this third particle is much less dense than the two main objects. It acts like a discrete gaseous object, moving from one place to another at a given speed. This speed is of course c.

If we define the field this way, instead of as lines, we can obtain a mechanical explanation of the E/M field. Mechanically and operationally, what we are interested in is the force imparted. Mass and charge are just characteristics invented to explain the force we measure. The force is the experimental fact; mass and charge are just abstractions, or ideas.

What we need to do to clean up the historical mess is a way to explain charge as mass. We need to jettison the whole ideas of charge, since it is not mechanical. It is needlessly fuzzy.

Quantum physicists will say that charge is not the equivalent of mass, since mass is caused by the ponderability of matter, or by its inertia, or by other equivalent ideas. Charge is thought to be caused by spin. M actually agrees with this distinction, but Miles Mathis does not think it matters here, mechanically or operationally, and this is why. If the electrical force is caused by a gas of ejected sub-particles, as MM proposed, then the term “charge” applies to the summed mass or momentum of those sub-particles. It does not apply to the spin. We don't need to know the mechanics of the spin in order to sum the momenta of the sub-particles. It doesn't matter what caused the momentum. In measuring and explaining the force, we only need to be concerned with the sum of the momentum.

Of course, once we have found a way to mathematically sum the momentum of the gas, we may ask how the gas is created. Then we are taken back to the spin of the elementary particles in the repulsing objects. It would appear that the spin causes the ejection or radiation. This would mean that charge is caused by spin; but charge is not spin. Charge is the mass or momentum of the ejected gas or radiation.

The only truly important distinction here is that mass is a quality that is normally applied to the main two repulsing particles (protons or electrons, say), whereas charge must apply to the mass of the field—the summed mass of the sub-particles. By this way of looking at it, protons and electrons do not “have charge.” Protons and electrons radiate sub-particles, and the summed mass or momentum of these sub-particles is the “charge.” Definitionally and logically and mechanically, charge is the summed mass of the sub-particles. In short, charge is mass.

And this is why charge acts mathematically just like mass. It is mass. To calculate the charge, you need to know the mass and the distance. You are given the speed, c. This allows you to calculate the momentum. Notice that the distance is actually used to calculate the mass, since distance is telling you how large your gaseous object is. The distance is not telling you that you have a force working through a distance, as with the definition of the Joule. No, the distance is in the denominator in this case. You are dividing the force by the distance, and this is because you are seeking the mass of your gaseous object.

The speed, c, is also used to calculate the mass of your gaseous object. Once again, this is because it is possible to calculate a mass if you are given a size (the distance) and a speed. The speed tells you the density at each dt. It is like a wave density. You have a certain number of sub-particles impacting your main particle at each interval. If you are given a length and a speed, then you have a time. This gives you a density.

You will say, yes, if you already know the force, then you can work back to find a mass for your gaseous object. You can find the mass of the electrical field that way. But if we don't know the force, then we can't know the mass, since we have no way of knowing the mass of each sub-particle. We must have something to sum, in order to find a density. If we don't know what each sub-particles weighs, we have nothing to sum. The speed and distance don't help us.

That is true as far as it goes, but the fact is that we can measure the force. That is why modern physicists have chosen to define everything in terms of the current. We can measure the force and the time and the distance. We know the speed also. Therefore it is quite easy to calculate the mass of the electrical field.

You will say, OK, but we still cannot know the mass of each sub-particle, since we don't know how many there are.

Once again true, but not really to the point. My point with this paper is not to assign a definite mass to the force-carrying sub-particle of the electrical field. It is to show that by giving mass to the electrical field we can totally dispense with charge, both the name and the idea. Charge is not a separate characteristic of matter. Charge is in fact the summed mass of these sub-particles.

This allows us to clean up the great mess of the electrical field. Rather than define a fundamental characteristic like charge by later interactions, we can resolve that characteristic into even more fundamental characteristics. It is topsy-turvy to define charge in terms of current, since charge is supposed to be the cause and current the effect. You do not define causes in terms of effects. My housecleaning defines charge in terms of mass, which not only puts a floor under something that was hanging—it also allows us to throw the hanging thing out as garbage. It allows for a great simplification of theory.

Not only that, but it allows us to throw out a lot of meaningless constants at the same time. By assigning mass to matter in the field, we avoid having to assign characteristics to the vacuum or to free space. Free space does not have permeability or permittivity or anything else. Free space is free space. It is space, and it is free. It it were permeable or permittive, it would be neither. Only when you refuse to assign parameters to charge does free space begin to take on characteristics. Only when you refuse to make sense about matter, does your space also refuse to make sense.

Now we are in a position to resolve the Coulomb and the statcoulomb. Above MM found that using only the dimensions of length and time
statC = L³/T² = M
C = L³/T³ = M/T

Since MM has shown how the mass of the radiation is calculated from the length and the speed, we can see where the difference comes from in these two equations. The statcoulomb comes directly out of Coulomb's equation. In that equation we are finding a single force. It has been called an instantaneous force, but since MM does not believe in instantaneous forces, he will call it a force over one defined interval. Since it is force over one interval, we are dealing with a velocity, not an acceleration. You cannot have an acceleration over one interval. That is why the first equation has one less time dimension in the denominator.

But remember that we took the Coulomb equation from an experiment that measured current in a length of wire. Since we have an extended length, we must also have an extended time. Although we may have a constant velocity and therefore an acceleration of zero, we still must represent that series of intervals in our math. That is why the Coulomb equation has the extra time variable in the denominator.

Before MM moves on, let one other mess must be cleared up. The permittivity of free space is
ε₀ = 1/c²μ₀ = 8.8541878176 × 10^-12 C²/Jm
Permittivity ε₀ is the ratio D/E in vacuum.
μ₀ is the permeability of vacuum, and has the value 4π×10^-7 N/A².
N/A² turns out to be m²/N, so that
ε₀ = 8.85 × 10^-12kg/m³
Or, if we express mass in terms of length and time, then
ε₀ = 8.85 × 10^-12 /s²

Why is the constant expressed that way? One, to reduce it to its simplest dimensions. Two, to show that it can be assigned to something else entirely. Since free space cannot have permittivity, by definition of "space" and of "free," that constant must be owned by something else in the field. That number is not coming from nowhere, so some real particle or field of particles must own it. To discover what it is, we notice that it looks like an acceleration that lacks a distance in the numerator. We want to transform that number into an acceleration, so we need meters in the numerator. So we start by multiplying by 1 meter. That gives us a sort of acceleration, but we aren't allowed to just multiply by 1 meter without a transform. We must insert the meter into the equation in a legal manner, you see. To do that, we must ask how the time we already had in the equation and the meter we just inserted are related to each other. How many meters are in a second? Seems pretty difficult until we remember that light knows the answer. Light goes 300 million meters in a second, and that is the answer. In one meter, there are 1/300 million seconds, so we multiply by 1/300 million. That will allow us to insert the meter into the equation legally.

If we do that, we end up with ε₀ expressed as an acceleration instead of as kilograms per cubic meter.

ε₀ = 8.85 × 10^-12 m/(3 x 10⁸)s² = 2.95 × 10^-20m/s².

That is lovely, because Gravity at the Quantum Level shows that this is about the value of gravity for the proton. Yes, ε₀ is not the permittivity of free space, it is the gravity field created by protons (and electrons). Earlier in that same paper "G is the Key to the Secret of Gravity" MM found a number for the "gravitational" acceleration of the proton of 4.44 x 10^-12m/s². This earlier figure is actually ε₀/2. Just look above, where ε₀ is 8.85 × 10^-12/s². MM had first found ε₀ by a variant method, and was not even aware of it at the time. Imagine having found ε₀ straight from G! MM's only problem in that earlier thought process was that he did not see how c fit into the solution, both as a correction of the dimensions and as a mechanism for measuring gravitational acceleration. It appears that as light is a time setter in Relativity, it is also a length setter here. All lengths are measured against c, and so we have to divide by c even when finding the gravity of the proton.

That clears up a lot of things, but let us look even more closely at the dimensions of the field in QED. The displacement field D is measured in units of C/m², while the electric field E is measured in Volts/m. As Wikipedia says, “D and E represent the same phenomenon, namely, the interaction between charged objects. D is related to the charge densities associated with this interaction, while E is related to the forces and potential differences.”
V = J/C = Nm//Ns/m = m²/s
If length and time are mathematically equivalent, as Minkowski taught, then we may reduce even further:
V = J/C = Nm//Ns/m = m²/s = m
So a potential difference is just a distance, like any other difference.
ε₀ = D/E = N/m²///m²//s/m = kg/sm² = m/s³ = 1/s²
So you can see that, no matter how we juggle these equation and dimensions, we find that the constants are misleading. They tell us meaningless or contradictory things. But if we change two words in the sentences above from Wiki, we can get a clearer picture of the two fields D and E. Let us change the word “charge” to “mass.”

“D and E represent the same phenomenon, namely, the interaction between massive objects. D is related to the mass densities associated with this interaction, while E is related to the forces and potential differences.”

Now, if we were talking about a gravitational field or any other field, and you said that you divided a mass density (or just a density) by a force or potential difference, you wouldn't thereby create a permittivity or permeability in your vacuum or your free space. The simple act of creating or theorizing densities and forces does not create a resistance in the vacuum. The gravitational field has densities and forces and potential differences, and yet the gravitational field requires no resistance. Why? Simply because Newton was kind enough to assign dimensions to his characteristic “mass.” He did not create a characteristic and then refuse to give it a dimension. Mechanically, his definition of mass is almost as empty as the definition of charge, but not quite. Newton tried to hide the fact that his mass was reducible to length and time by giving his constant a very strange dimension, but in the end these dimensions of G reduced to 1. This kept his constant just a fancy number, with no dimensions.
G = L³/MT²
M = L³/T²
G = 1
Since his constant has dimensions that are reducible to one, his field has no resistance or any other qualities. All the qualities are assignable directly to matter in the field.

The same is ultimately true of the electrical field, but physicists will not just come out and say so. In fact, they have preferred to imply, in the constants and fields they have created, that the vacuum does have characteristics. It has permittivity and permeability, which, if they really existed, would be types of resistance. But the electrical field has no resistance that it does not create itself, with the same matter that is creating the field in the first place. The only thing that resists the sub-particles are other sub-particles. The only thing that resists the gaseous object is other parts of the same object. The gas is material and it therefore resists itself. The radiation interferes with itself in a purely physical way, with no help from the vacuum.

When a Standard Model gas, made up of normal molecules, resists itself, we do not try to assign this resistance to the vacuum. We do not make up absurd abstractions like the permeability or the permittivity of the free space. We simply assign the resistance to molecule collisions. We could do the same thing with the electrical field, but we have so far preferred not to. Why?

Everyone knows that it is because once you admit that the E/M field is composed of radiation, you have to explain why the proton and electron aren't diminished by this radiation. We can create the sub-particle called the quark with no guilt or sin, since it doesn't immediately threaten to undermine the conservation of energy. But if the electrical field is composed of radiation, and if this radiation has mass, why doesn't the proton lose mass in radiating it? It is simply to avoid this question that the great mess of the electrical field has been left to sit. Physicists prefer a big mess and a big cover-up to an honest question.

[To read more about Maxwell's displacement field D and the constant ε₀, you may now go to Miles Mathis site to read Maxwell's equations are disguised Unified Field equations. There MM shows that D actually is the charge field, and that Maxwell's equations are unified.]

Now let us show the first major outcome of MM's change in theory. MM has shown that charge must have a mass equivalent. Charge is the summed mass of sub-particles that are impacting the objects being repulsed or attracted. The electrical force cannot be imparted by an abstract field or a mechanically undefined charge; it must be imparted by something capable of imparting force, and the only thing that is mechanically capable of this is mass or mass equivalence.

If we give the radiation that causes the electric force the mass required to achieve this force, then we have a form of mass that must be opposed to the mass that creates the gravitational field. By that MM means that the two fields are in opposition to each other mechanically. One must be negative to the other. By this MM does not mean anything esoteric. MM is not creating some sort of mystical negative mass. MM only means to point out that every particle's radiation must have mass, and that this radiated mass creates a vector field that points out, whereas the gravitational mass points in. We already know that, in a sense. However, we have not included the idea in the math.

In another paper MM has theorized that the E/M field is always repulsive, at the level of quanta. All forces are ultimately caused by bombardment. Electrical or magnetic attractions are always only apparent, caused not by real attraction but by relative attractions. This means that the proton does not actually attract the electron. It only repels it much less than it repels other protons. This leads to an apparent attraction, since the (“gravitational”) expansion of the proton allows it to capture the electron, but does not allow it to capture other protons. This leads to the appearance of attraction, in the dual field that is the gravity-E/M field.

When we measure the mass of a particle—either by using a scale or by looking at deflection—what we must be measuring is the sum of the two fields. We are measuring the gravitational force minus the force of the E/M radiation. This is simply because (to take the example of the scale) the radiation is bombarding our equipment, offsetting the “weight” of the particle itself. It is as if the particle is a little rocket, and our scale is the launch pad. The particle has it engines on all the time, and therefore we are not measuring the full weight of the particle. We are measuring the gravitational force minus the radiation force.

Notice that the rocket analogy is not quite right, since a scale on the launch pad would actually measure the force of the exhaust. But when we are calculating the mass of a particle, we are not putting it on a scale in that way. At the quantum level, we are measuring its deflections from other particles, and calculating its mass from the summed forces. But these forces must be compound forces. The expansion of the quantum particle makes it appear to attract all other particles; its radiation makes it repel all other particles. The total force is a vector addition of this attraction and repulsion.

What this means is that the true mass of the particle must be greater than the mass we measure or calculate with our instruments, whatever they are. If you take the mass of the particle to mean only its ponderable, gravitational characteristics, or only its force due to expansion, then that mass must be greater than the one we always measure. We are measuring the mass of the particle minus the mass of its radiation. Therefore its true mass is the measured mass plus the mass of the radiation.

In the end, this is not because the radiation mass still belongs to the central mass even after it has been radiated—not in any sense at all. No, it is simply an outcome of the math. It is due to vector addition and only to the vector addition. It is a straight outcome of the fact that the expansion creates an apparent gravitational field with vectors that point in, and radiation creates a real bombarding field with vectors that point out. This makes the true mass of the central object the addition of the absolute value of both fields.

Once you absorb that, it is time to consider the fact that calculating the true mass in this way must vastly increase the total mass of the universe. Over any dt, the mass of a given object is given by the expansion of the object in that time. But we can only measure the force due to expansion (gravity) minus the force due to the mass or momentum of all the radiation in that same time. Therefore the true mass must be the measured mass plus the mass of the radiation.

Also notice that this change in mechanics gives us a double addition of mass to the universe, since we gain both the mass of the radiation itself as well as the higher true mass of the radiating particle.

Both these statements are true:
1) The mass of the radiating particle must be greater than the mass measured by our instruments, since our instruments measure a compound mass.
2) The radiation itself has mass or mass equivalence due to energy, which is a second addition to the total mass of the universe. A radiating particle does not lose mass, which means that the “holes” left by radiation are filled by some creative means.

Radiating quantum particles do not dissolve or diminish. This is known. Therefore "creation" happens at all times, from every material point. The universe is banging all the time.

Of course this immediately and simply explains the "mass deficit" in the universe and in current theory. We don't need massive amounts of dark matter or any other ad hoc fixes, since MM has just shown the missing matter and energy. All we had to do is define our electrical field as a mechanical field instead of as pencil lines and we could have avoided this mess from the beginning.

But the fact is, the E/M field, like the gravitational field, obeys the inverse square law because the objects in the field are spheres. Coulomb's objects were spheres, and electrons and protons and photons are also spheres. The field emitted by the electron is spherical, and the field emitted by Coulomb's objects is spherical. This determines all the charges and forces.

The reason Coulomb's equation is so simple is because the spherical nature of the field allows us to scale up and down using only a radius or a diameter, as MM will show below. Coulomb was measuring a force between two small balls. The force was a force measured at the macro level, between macro (visible) objects. But this force is actually a summed force caused by a field of forces. It is caused by a bombarding field. Coulomb's balls are made up of billions of smaller balls (atoms), and the force at the atomic level is a bombardment of these smaller balls by even smaller balls (photons). To find a force on one atom, we need to know the density of the field of photons relative to the size of the atom. How many photons are impacting it each second? To sum up from the quantum field to the macro field requires we sum all these collisions. Since charge in this problem is defined by field density, we sum the field. But there is a problem. Density is a relative term. It is relative to volume, and volume is relative to radius. So a charge measured at the macro level is not the same as a charge measured at the quantum level.

This is where Coulomb's constant enters the equation. We now define charge in terms of current, one Coulomb being one Ampere second. This is a crazy way to define charge, since current and charge are two different things, but the operational crux of this definition is that current is a macro-phenomenon. In measuring Amperes, we are NOT measuring quanta: we are measuring changes in macro-objects like batteries and voltage meters and so on.

Therefore, to get a force from charges defined in this way, we have to multiply our charges by a scaling constant. The scaling constant takes the macro-density (the density of the charge field relative to macro-objects) and takes it down to the quantum density (the density of the charge field relative to protons and electrons and atoms). This gives us a correct force, one we can then sum.

If our macro objects are spheres, we can achieve this sum simply by the scaling up of the charge. In this way, you see that the force IS the charge. Force and charge aren't fundamentally different parameters: force is just charge in a given space. All we have to do beyond the scaling is let the field diminish with the inverse square law. That is to say, the field is emitted, and so it must lose density as it expands into space.

In sum, defining charge in terms of current doesn't really give us charge. But it does tell us a field density of the charge, at the macro-level. We can't get a force from this macro-field density, but we can get it from the quantum density. The density of the charge field relative to the size of the atoms will be much greater, and so will the force felt. This is the force we want, since it is the real force. So we simply multiply by a number that will give us the quantum density from the macro-density. This is what Coulomb's constant does. And it does it by comparing radiuses only. We need only ask the radius of the atom relative to the radius of our macro-objects: with spherical objects the radius will give us the volume and therefore the density difference.

So, Coulomb's constant tells us directly that the charge field at the atomic level is 9 x 10⁹ relatively more dense than the charge field at the macro-level. And this tells us that the atom is 9 x 10⁹ smaller than the macro-world.

But there is still some confusion here. How big is the macro-world, exactly? According to MM's analysis, the macro-world is defined in Coulomb's equation by his balls, which were about 6 mm in diameter.¹ But Coulomb was not able to calculate Coulomb's constant from his experiment. He could not measure charge and force, so he had no way to find k. He only proved that the repulsion was inversely proportional to the distance of separation. The constant was calculated much later, once we knew the charge on the electron and the Bohr radius and so on. And the diameter of Coulomb's balls did not come into that calculation.

You may know that the constant was calculated using the charge on the electron, but we are never told that the constant is related to the Bohr radius. In MM's paper on the "Bohr's Three Mistakes", MM showed that Coulomb's constant depends on the Bohr radius. As a number, it is the inverse of the Bohr diameter. But this means that Coulomb's constant is scaling up to the size of 1 meter, not 6 mm. That is a difference of 170 times.²

You will say, “So what? Normally Coulomb's constant has nothing to do with sizes or lengths, but even if we admit that this mathematical side street exists, how is it possibly pertinent? Does the E/M field act differently at 6 mm than at 1 meter?”

Yes, it does. Not only have MM shown in Newton's law is a Unified Field of Gravity and E/M that the field is different at different sizes, but more importantly, the density must be different. We are at a larger radius and a larger volume, which must create a smaller field density.

MM has shown that both Coulomb's equation and Newton's equation are unified field equations. Both of them contain the E/M and gravitational fields. Newton's equation hides the E/M field in the mass variables, and Coulomb's equation hides the gravitational field in the charge variables. Masses have both volume and density, as do charges, and in each equation the two fields can be separated along with volume and density. Once we do this, gravity varies only with radius, and E/M varies with density. But this must mean that they do not stay the same size, relative to each other. They scale differently. This is why gravity is larger at large scales and E/M is larger at small scales. We already knew this about scaling, we just didn't have a way to show it in a unified field.

Since Coulomb's equation is a unified field equation, it matters very much what size we are dealing with. Even a difference of 170x is significant. The relative sizes of the two constituent fields are different, and so the unified field will not act the same. There will be no variance from the inverse square law, but due to the form of the equation, there will appear to be a variance from it. To be specific, the denominator of the equation will follow the inverse square law perfectly, as it must, but the numerator will betray the equation. This is why you get different curves in different experiments: the objects in the experiments are not the same sizes. The curves roughly follow the inverse square law, but a 1 mm charged object will not act like a 1 m charged object or a 100 meter charged object. The reason is that these objects don't act the same as unified field objects.

Beyond that, a 6 mm object is not equivalent to a 1 meter object in another way, a way that strongly impacts the operation of this constant. For Coulomb's constant to work correctly, it must transform between the right levels. It must take us from the atomic level to the experimental level. In Coulomb's experiment, this would be between the Bohr radius and 6 mm. Using the current Bohr radius [5.29 x 10^-11m], that would be 8 levels (taking each factor of ten as a level). But the current constant is the inverse of the Bohr diameter, which, taking us up to 1 meter, takes us through 11 levels. The constant is too big for Coulomb's experiment. Either the constant is too big or the Bohr radius is too small, or both.

In the paper "Bohr's Three Mistakes", MM shows that this off by about 170x. Amazingly, MM discovered this in an analysis that had nothing to do with Coulomb. MM was re-doing the math for the Bohr magneton, by correcting the angular momentum equation, and found the number 170 that way. Only afterwards did MM realize that this connected to the Coulomb equation.

The Bohr radius is 170 larger than we thought, and 1 meter is 170 times larger than Coulomb's balls. The standard model pushed the balls up three levels, when they should have pushed the Bohr radius up three levels.

What this means is that Coulomb's constant is not a constant. It is a variable. You have to consider what force you are talking about, what force you are seeking, and how it is measured. If you are applying Coulomb's equation to quanta, as they effect each other through the charge field, the constant is one. You don't need a density transform, since you are already at the quantum level. If you are applying the equation to quanta as they affect macro-objects (like detectors), then you have to consider the size of your detector. If you are applying the equation to macro-objects, you must consider the sizes of your objects. If you are seeking Coulomb's constant relative to 1 meter, then the constant is 1.11 x 10⁸. Current math is wrong. Using the correct math, we find that the Bohr radius is 9 x 10^-9 m, which looks an awful lot like Coulomb's constant, 9 x 10⁹. But that does not increase our density by 9 x 10⁹. It increases it by 1.11 x 10⁸ [1/(9 x 10^-9) = 1.11 x 10⁸]. By the same token, if we apply Coulomb's equation to Coulomb's balls, we have a density difference of only 6.5 x 10⁵. If we have an equivalent charge on the Earth, then Coulomb's constant increases to 7.08 x 10¹⁴. As you see, Coulomb's constant is not a constant.

The historical fact is that Coulomb's equation is hardly ever used in real life, and when it is used it is misused. It isn't used because there is no place in the equation to represent the fact that charge can vary. Charge is not a constant at any size. Coulomb transferred a small static charge to his pith balls with a pinhead, but there is no indication that he could not have transferred more or less charge. A sphere 6 mm in diameter could hold any range of charge, depending on its elemental makeup, its density, and the charge applied. You will say that Coulomb's equation represents the charge, but it is not just a matter of the charge size or the separation between charges, it is also the charge density. In other words, the charge size relative to the size of the object charged. If you vary the “constant” like MM is doing, you can represent this density, but not otherwise. With a constant that is constant, the equation cannot work, except by accident (on an 81 meter object).

If we were dealing with magnetism, for instance, we would have to differentiate between H and M, where H is the magnetic field strength and M is the magnetization per unit volume. But Coulomb's equation ignores this difference. Charge is said to create both electricity and magnetism, but in the historical and fundamental equation of charge, we have no possible expression of M or its charge equivalent. We know that electricity and magnetism both have density considerations like this, and that both are caused by charge, but we do not express density in the charge equation.

To see how wrong the Coulomb equation is, let us look at an example problem in a textbook. In this problem, the author calculates the force between an orbiting electron and a hydrogen nucleus.

F = (9 x 10⁹ Nm²/C²)(-1.6 x 10^-19 C)(1.6 x 10^-19 C)/(5.3 x 10^-11 m)²

= -8.2 x 10^-8 N

Just as a comparison, this is about the same force between Cavendish's balls in his experiment. He had 350 pounds of mass separated by a few centimeters, and found a force of about 7 x 10^-8 N. This textbook expects us to believe that there is an equivalent force between a single proton and electron. If, as MM have shown, k is a scaling variable, what is it doing here in this equation? We have nothing to scale. If it is not a scaling variable or constant, what is it? Why is it here? Why does no one ever ask this question?

[To see the correct derivation of the force between the electron and proton, see Gravity at the Quantum Level but get ready to be shocked.]

Furthermore, if the E/M field is an emission field, as it must be, how can the electron and proton emit the same field when they aren't the same size, mass, or energy? Shouldn't the proton have a stronger field? If not, why not? And if we have an emission field, how do we get attraction? An emission field could only cause repulsion, right? There are answers to these questions, as MM has shown elsewhere, but the standard model never even asks them.

If the constant k is just a cgs kludge, as has been claimed by many physicists and engineers, why does it happen to be equal to the inverse of the Bohr diameter? They might answer that it is because you can invert it and put it in the denominator, so that we have

F = q²/r³

They will say that the charge has to dissipate into three dimensions, not two, so the cubed radius gives us a volume. But that only appears to work in this one case where the radius is the Bohr radius. The equation is supposed to work for all charges, not just the charge on the hydrogen nucleus. We use the same constant when we calculate larger charges, as in this example from the same textbook:

F = (9 x 10⁹ Nm²/C²)(-4 x 10^-6 C)(-3 x 10^-6 C)/(.5 m)² = .43 N

The constant k is not a third dimension there, is it? We can't combine it with the radius, can we?

While the cgs system is preferable in many ways, it does not clear up the mystery here, not in the form of a kludge or in any other way. The cgs system uses the statcoulomb instead of the Coulomb, and it does indeed get rid of the constant, but it does so by defining the charge in terms of the force, which is of course circular.

“If two stationary objects each carry a charge of 1 statC and are 1 cm apart, they will electrically repel each other with a force of 1 dyne.” So instead of defining charge in terms of current, we define it in terms of force. This means that the mystery is not solved, it is simply swallowed. With electrostatic force, the Coulomb is preferable in one way: it makes the problem a bit more transparent. The Coulomb leaves the door open a bit. Without that MM would have been very unlikely to discover the things he has if he had been limited to the cgs system.

So it is not only the newer SI system that blocks questions about the E/M field, it is also the old cgs system. To show once again how far the current standard model will go to block questions, notice this from Wikipedia, under the heading “statcoulomb”:

Performing dimensional analysis on Coulomb's law, the dimension of electrical charge in cgs must be [mass]^1/2[length]^3/2[time]^-1.

That is misdirection, since that can be reduced. Maxwell showed that we can easily do a dimensional analysis on mass, using only Newton's equations. Mass is [length]³[time]^-2. If we substitute that into Wiki's analysis and reduce, we find that electrical charge is equal to mass. Why is Wiki, the mouthpiece of the status quo, so keen to avoid telling you that? Why is Wiki like all standard texts, online and off, in misdirecting you from the truth?

And another question never answered by textbooks: why is the difference between the Coulomb and the statcoulomb ten times the speed of light or 10c? How did c get into an equation of charge and length? The standard model wants you to think it has something to do with vacuum permittivity or one of the other meaningless constants, but it actually comes from the fact that the charge field is material. You can calculate a force from a density only if you know the velocity of the field. In this case, that velocity is c, and that is how it enters this equation. In MM's use of the constant k above as a scaling constant, we could ignore c, since it was the same at all densities and volumes. But when you get down to the groundwork mechanics, you find that you need the velocity in order to sum the force. To get the force, you have to know how many particles are hitting your object over some time interval. The density at a given volume won't tell you that. But if you have a velocity and a density, you can calculate the force, since you then have a field strength. You have both the area of impact and the time of impact, you see.

The standard model must hide this, since bringing a velocity into the equation should destroy the virtual nature of the field. If the field has a velocity, it must be a material field. Everything with velocity has energy, and everything with energy has either velocity or mass, or both. So you cannot logically propose a virtual field that has no energy and no mass equivalence. If your field has velocity, it has energy, and if it has energy, it has mass equivalence. If it has mass equivalence, it is not virtual. If it is not virtual, it must take part in all interactions mechanically, and obey all the rules of mechanics. If the charge field becomes real like this, QED and QCD immediately fall.

Conclusion: even if one disregards all MM's new theory and math, the very fact that Coulomb's constant can be shown to be the inverse of the Bohr diameter means there must be a mathematical and mechanical connection between radius and charge. That is to say, a direct, causal connection between length and charge. And not just a connection of the charge separation, as we already knew from the inverse square law. No, the Bohr radius has nothing to do with the charge separation or the inverse square law. The Bohr radius is the atomic radius (of hydrogen), and the only way it could be mechanically connected to Coulomb's constant is if the charge field is an emitted field, with a real density and therefore a real mass.

If the charge field had no mass or energy, we could not connect it to any length at all, not the Bohr radius or any other radius. Any length necessarily implies an extension, and things without mass and energy cannot have extension, or be related to things that do. We are not taught this connection of the Bohr radius and Coulomb's constant because it is known to be a tip-off. If physicists were taught that the Bohr diameter is the inverse of Coulomb's constant, all the questions asked in MM's introduction would be asked by everyone. Everyone would immediately begin to see that the E/M field must be mechanical and physical: that it must occupy space and exhibit real density. If they did this, QED would fall overnight and be replaced by a theory with a real field particle.

(For more on how the E/M field is unified, go to Maxwell's Equations are Unified Field Equations)

Charge at the Quantum Level

For more than two centuries now, since the time of Franklin, charge has defined the electrical force, and for just as long it has come in two forms: positive and negative. We now give the positive charge to a particle: the proton or nucleus; and we give the negative charge to the electron. But beyond that, we haven’t made much progress since Franklin. QED is an E/M theory, it is true, and QED has discovered many things. But QED has not been able to put a mechanical foundation under the positive and negative signs. We still draw protons with little +’s on them and electron’s with little -’s, as if that explains anything.

The reason for this lack of mechanical progress is that QED has never been interested in mechanics. It gave up on mechanics 80 years ago. It is interested in probabilities. This is shown by the ludicrous state of the concept of charge. To explain the force between the electron and proton, the standard model now makes use of the “messenger photon,” a so-called virtual particle that is made doubly virtual by always being “summed over” in a Feynmanian sense. This allows the standard model to have a force with no energy transfer. Since the mediating particles are virtual, with no mass or mass equivalence, the energy and forces are also virtual. The only thing that is not virtual is the acceleration, which we need to keep for our equations.

The reason the standard model so flagrantly avoids a real field here is to avoid assigning that field mass. Physicists must be aware that you can’t have forces without masses or energies, or the equivalent, but they also know that giving the charge field mass or energy of its own, beyond some virtual fudging, would doom the entire house of cards that is QED and QCD. If you give the charge field mass or energy, then quanta must be radiating energy. If they radiate it, they lose it. QED and QCD cannot explain this loss of energy, and don’t want to explain this loss of energy, so they ignore it. It would require a re-do of decades of theory and equations, and nobody wants that. So, in their minds, it is preferable to be caught red-handed proposing forces and accelerations without masses or energies. They have such high opinions of their own abilities to convince, and low opinions of their audiences, that they really believe they can say these things out loud, with no curtains or magic wands, and not even have to break stride.

Any honest person, supposing one still exists in physics, would see this for the great feat of magic it is. By using virtual particles, the standard model achieves a force and a motion with no energy transfer. It achieves a kinematics with no mechanics. It achieves an answer with no explanation, a series of airy words with no physical content. The messenger photon appears out of nothing (achieved by some wish of the nucleus) moves in some ghostly fashion out to the electron, whispers something to it through the void, and then conveniently disappears. With such a transaction, we do not have to worry about conservation of energy or mechanics or force by contact or any of the old bugbears of physics. In this story, charge is nothing more than a black flag waved by a ghost.

What sort of physicists could be satisfied by such a story, much less proud of it? How can a theory (QED) which has made so little progress on the central question make any claim to success, much less completeness? The standard brag now is that quantum physics is so successful there is nothing left to do. Everyone has to go into string theory now in order to stave off boredom, we are told.

The key to unlocking this mystery is contained in the realization that the idea of attraction is non-mechanical. In Newton's law is a Unified Field of Gravity and E/M MM pointed out that Newton’s friend Jonathan Swift knew this centuries ago. Swift warned Newton of this, cleverly disguising his advice within the pages of Gulliver’s Travels (as he did with much of his good advice). Unfortunately, Newton did not heed this advice, and no one since has paid it the proper attention.

This advice collides with “charge” in two separate places. Firstly, and most obviously, it disallows charge attraction. All attractions must be only apparent--the result of complex motions. The pluses and minuses of E/M theory are not only empty attributes, they are impossible attributes.

But Swift’s advice collides with the idea of charge in another place. The gravitational field has also historically been defined as an attraction, and it turns out as MM shows in G is the Key to the Secret of Gravity that gravitational field has been hiding at the quantum level as well. Therefore, in order to solve the problem of charge, we have to uncover gravity at the quantum level, and then redefine it so that it is no longer an attraction.

In Newton's law is a Unified Field of Gravity and E/M MM shows that what we have always called the gravitational field at the macro-level is in fact a compound field that includes both gravity and the “charge” field. That is, it includes the field mediated by the messenger photon. Newton’s gravity equation can be expanded, with G as the transform between the two fields. Once we re-expand the equation, we find that “mass” is hiding two separable features, and that one of them goes to one field and one goes to the other. Specifically, if we write mass as density x volume, the volume goes to the gravitational field and the density goes to the charge field (or what MM calls the foundational E/M field). Gravity is no longer dependent on density; it is proportional to volume or radius, and nothing else. Density is important only in the E/M field.

The way that all this impacts the problem of charge is that it must be redefined:

The charge field is a bombarding field only. It is always repulsive; never attractive. It is caused by radiation of these messenger photons, which MM re-dubs as B-photons (for bombarding photons).

The repulsion is caused by an old-fashioned force by contact. Of course this means that the B-photons are not virtual: they have energy, mass equivalence, and even radius which is derived in G is the Key to the Secret of Gravity. This was achieved not by the usual slipshod math, not renormalized, not summed over or not by any other dreamed-up method. This radius is taken right out of Newton’s own equation! Newton himself knew of this number, though he never applied it to the right radius.

The other thing that my unified field allows us to do is discover the gravitational field at the quantum level. It turns out that once we re-expand Newton’s equation into its two constituent fields, we can apply it at the quantum level directly. (See Gravity at the Quantum level.) Because the gravitational part of this compound field is now dependent upon radius alone, this field increases in size at the quantum level by about 10²². This makes it a major player in the quantum field once more.

These two fields allow us to explain charge mechanically because they are in vector opposition. Gravity causes an apparent attraction and the B-field causes real repulsion. This field differential is true at all levels of size, quantum and cosmic. The total force is

F = H - E

Where H is the new solo-gravity field, separated out from the compound field. F is just the F of Newton’s equation.

Note that MM has avoided gravity as a real attraction by inverting Einstein’s field. By using Einstein’s equivalence principle, the universe can be turned inside out, mathematically. In one pass, every gravitational acceleration vector in the universe can be switched. The math is unchanged, including most final equations of General Relativity; but we replace curvature with expansion. Instead of giving the curvature to the time/length graph, we give it to the time/size graph. The time/length graph reverts to a rectilinear Euclidean space, making our equations so much shorter and easier. We only have to get used to the idea of universal expansion. Big Bang theory and other cosmological theory has already accustomed us to thinking of an expanding universe, so it is not any great jump in accepting that expansion from every point, instead of only as a whole. But if you have difficulty making the jump, see an example of it's usage in The Aberration of Starlight is an Expanding Earth.

According to MM's re-expansion of Newton’s equation, we now have a compound field at the quantum level, with the two fields in vector opposition. How does this solve the charge problem? It solves it quite easily, since we can now create opposite potentials simply by size differentials. What we have is a small electron and a large proton (to simplify). Both are radiating B-photons. Let us say that the radiation from the electron is relatively negligible, so that we can look only at the radiation from the proton. The proton is emitting a bombarding field that tends to drive off all particles that come near. But it will drive off larger particles more successfully than smaller particles, since the smaller particles will encounter a smaller cross-section of the field. Because the field is a field of discrete particles, a small enough electron could actually dodge the field almost entirely. But we will not imagine the electron is that small. We assume, for now, that it is much larger than the B-photon, and cannot dodge the field.

Also remember that any other proton that enters the field of our first proton will also be emitting its own B-field. These fields may interfere to some extent, but we would still expect the combined field to be more repulsive than either field taken alone. This must mean that any protons will be driven away from each other much faster than an electron will be driven away.

You will say that we still have repulsion of both the electron and the proton, but we have not brought the newly upgraded gravitational field into the mix. This field is going to cause an apparent attraction to all particles, just like the traditional field. All particles are going to appear to “fall” toward our gravitating proton, and they are all going to fall at the same rate. Standard gravity theory, so far. But let us use Einstein’s equivalence principle to reverse only our terminology. Instead of saying that all objects are falling toward our proton, we say that our proton is chasing all objects at the same rate. An acceleration in one direction is equal to an acceleration in the other direction, in a rectilinear field.

So, in order to explain both positive charge and negative charge, we only have to propose that the proton is chasing the electron fast enough to catch it, but not fast enough to catch the proton. This gives us an apparent attraction of one, and an apparent repulsion of the other.

Another way to state this is to give numbers to the two repulsions. Say the repulsion of proton by proton by the B-field causes an acceleration of 10. And say that the repulsion of electron by proton by the B-field causes an acceleration of 2. All we have to propose is that our central proton is accelerating gravitationally at a rate greater than 2 and less than 5. Anywhere in that gap, we will see repulsion of the two protons and an attraction of the electron. That is the simple mechanical explanation of charge.

What about current in a wire? You will ask how my theory explains that. Again, quite easily. Free electrons travel at high speed in a conducting wire, or any conductor, because the B-field is moving in only one direction in that substance. The B-field acts as a river, moving the electrons along by direct contact. This B-field river can be created in any number of ways, either by having lots of radiating particles at one end of the wire and few or none at the other, or by directionalizing the B-field through the shape of the molecules in the substance. Some molecules block certain directions of the B-field, simply by getting in the way. Of course this a great simplification; but once this field is understood, the questions are no longer difficult.

Vienna State Opera House 2021 How MM discovered the charge field

I get emails from spotty readers, asking me “Where is this charge field of yours? I can't seem to find it in the field equations or in the data.” So I will take this opportunity to rerun for you some of the sweetest math I have ever done. This will show you where the charge field is hidden, both in the math and the data. These are the equations which, if I live long enough, I will write on some big blackboard with dramatic flourishes, in a grand auditorium (I would like to suggest the Vienna State Opera House), in front of a bank of cameras. I would also like to suggest that the world not wait too long to figure this out, since it will be so much more cinematic if I have a full head of “scientific” hair when this happens. The clock is definitely ticking.

But seriously, these two proofs of the charge field have been separated so far, buried in longish papers that few may be able to get through. I have linked them, but that probably isn't enough. And so I thought it best to put them here side by side, in a short paper that may be readable.

In short, this is how I developed the number .009545m/s² for the charge field of the Earth, in two different papers, in different years, on different continents, working on separate problems, and with unrelated math. I will try to insert flourishes, and if we are imagining a time too far in the future, you can imagine me in a wig. Don't forget to applaud at the end.

The first calculation came about after I had been staring at the Moon for 72 hours straight (not really, that was a flourish). It occurred to me that perhaps Newton's equation for gravity—the famous F=GMm/r²—was already a unified field equation. If it was true, how could I tease the E/M field out of that equation, without going to a lot of trouble? I am lazy that way. I thought, why not just compare the current numbers for the Earth and the Moon, with the added assumption that gravity by itself was proportional to radius? In other words, if we take E/M out of Newton's equation, we are left with gravity by itself. What is gravity by itself? Well, it might be a force that was dependent only on size. Acceleration is dependent only on distance, gravity is an acceleration, and radius is a distance. So if gravity is an acceleration, it should be dependent only on distance. The mass dependence was always fishy, and we accepted it only because Newton told us to. What I mean is, we know that a=v²/r isn't dependent on mass, so why should F be dependent on mass? You will say it is because F=ma. There is the mass dependence. But if F=ma is also a unified field equation, and also includes E/M, then my point remains. Perhaps the m goes with the E/M field part of the equation, and it has nothing to do with gravity?

To test this, I just calculated the corrections we would have to make to the Earth and Moon to make it work. If I were wrong, I would find out very quickly, because I wouldn't be able to make the numbers work. You can't really push equations like this: they either work or they don't. If I were right, then the gravity of the Moon should be:
g_E / g_M= 3.672
9.8 m/s² / g_M = 3.672
g_M = 2.669 m/s²

That's much higher than the current number, but if I could show that the E/M field of the Moon offset that, bringing that number back down to the current number, I would be in high cotton. So what I did is assume that the E/M field fell off by the fourth power. Again, that assumption will either work or it won't. There is nothing in between. You can't push this kind of math, because the first assumption— that gravity increased with radius—gave me a definite gap to fill. The number 2.669 is solid, and it can't be moved. My second assumption also will give me a definite number. Either those two numbers offset or they don't.

I have postulated that the gravitational part of this acceleration should be proportional to the radii.
g_E / g_M= 3.672 (accepted value)
thus
g_M = .2723 g_E

****** And I have just postulated that the E/M field is proportional to 1/r⁴.
E_E /E_M = 1/3.672⁴ = .0055
E_M = 181.81 E_E

But that last equation is assuming that the Earth and Moon have the same density. So I must now correct for density.
D_E / D_M = 5.52/3.344 = 1.6507 = 1/.6057
E_M = 110.12 E_E

****** So, we just substitute:
.2723 g_E - 110.12 E_E = 1.62 m/s²
g_E - E_E = 9.8 m/s²

.2723g_E - .2723E_E = 2.6685 m/s² [subtract the two equations]
-109.85E_E = -1.0485 m/s²

E_E = .009545 m/s²
E_M = 1.051 m/s²

g_M - E_M = 1.62 m/s²
g_M = 2.671 m/s²

The proof is complete. It worked. And I have a number for the charge field of the Earth. It's pretty small, which explains why it has remained hidden in most cases.

Now, in the years after I wrote this paper, I discovered that this number could be found in other places. For instance, it explained the gap in the Bohr magneton. The Bohr magneton is just the calculation of the magnetism of the electron from field equations. But the magnetic moment of the real electron is found to be a slightly different value. In other words, the math didn't match the data. And, as it turns out, the gap between the math and the data was my number: .009545. The mathematicians forget to include the charge of the Earth, since they didn't know about it. It was hidden inside the field equations.

Soon after that, I found the number in another place, this time with some new math that had never been done before. In a paper on atmospheric pressure, I needed to calculate the total weight of the atmosphere as a fraction of g. To do this, I assumed that the atmosphere was contained by the ionosphere above. I let the ionosphere start at 50km. Then I calculated the lateral freedom of the atmosphere compared to the vertical freedom.

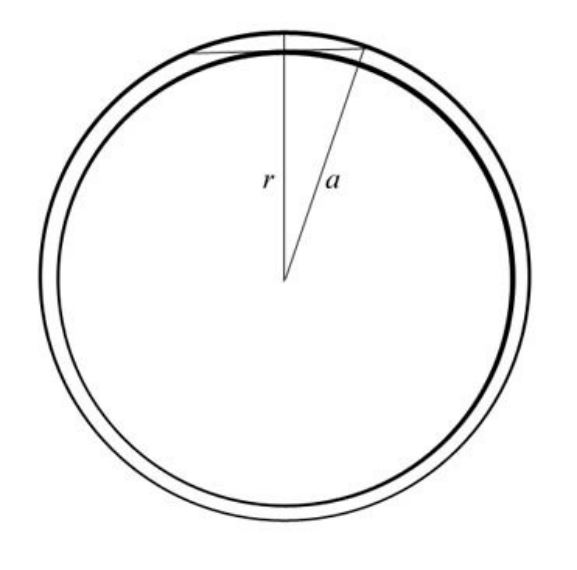
If r is the radius of the Earth, and a is the radius of the atmosphere at 50 km, then we can find the third leg of the right triangle very easily. It is 800 km, and we double it to find the full width: 1600 km. This means that the atmosphere has 32 times {1600/50} more lateral freedom than vertical freedom. But that is only in one plane. If we make our diagram three dimensional, we must square the lateral freedom, giving us 32² . If we assume this allows the gas to express only 1/32² of its weight, then we find a downward field of about .009550 m/s² {9.78/32²}.

At first I was astonished to find that number. I didn't expect it, I was just playing with an idea, as usual. I expected the problem to be more difficult than that. But of course that number has to match my number, since the weight of the atmosphere down has to equal the charge force up. Otherwise the sky would fall! This way we have equilibrium, and a sky that appears to weightless—because it doesn't fall.

In this way, I had confirmation of my number from a problem that was unrelated to my first proof. The Moon and the atmosphere are two separate problems, as I hope you will agree.

And there you have it, proof of the charge field, both in the math and in the data. I used current data and I used current math, just updating it with a little linking math of my own. I hope that got through to you. If it did, please call the Vienna State Opera House

Next: Maxwell's equations are disguised Unified Field equations or Return to main page