Maxwell's equations are disguised Unified Field equations
© Miles Mathis First published April 18, 2013 Here it will be shown that Maxwell's equations are also disguised
unified field equations by studying Maxwell's lesser known displacement current. The indication of this was the inclusion of ε0,
which MM has shown really stands for Newton's gravity equation is a disguised unified field equation:
Please note that this paper is a simplification by me of a paper or papers written and copyrighted by Miles Mathis on his site. I have replaced "I" and "my" with "MM" to show that he is talking. All links within the papers, not yet simplified, are linked directly to the Miles Mathis site and will appear in another tab. (It will be clear which of these are Miles Mathis originals because they will be still contain "I" and "my".) The original papers on his site are the ultimate and correct source. All contributions to his papers and ordering of his books should be made on his site.
(This paper incorporates Miles Mathis' disp paper and disp2 paper)

Maxwell
MM's previous proofs:
Newton's gravity equation is a disguised unified field equation:
"Newton's law is a Unified Field of Gravity and E/M"
Coulomb's equation is a disguised unified field equation:
"Coulomb's equation is a Unified Field equation in disguise"
The Lagrangian/Hamiltonian is a disguised unified field equation:
"Proof that the Lagrangian and the Hamiltonian are false"
"G is the Key to the Secret of Gravity" . Although it has been assigned to the
permittivity of free space, the number actually stands for the strength of gravity of a baryon. If gravity
is in Maxwell's equations, they are unified.
D = ε0E + P
That is Maxwell's equation for the electric displacement field, where E is the electric field intensity, P is the polarization of the medium, and ε0 is the permittivity of free space.
The alarm bells went off for MM soon as he saw ε0, since MM has shown in the paper on Coulomb above that the permittivity of free space is misassigned to free space. We should have known that, since free space cannot have any physical characteristics like this. If it did, it would be neither free nor space. In writing the unified field equations, MM has shown that the constant ε0 actually stands for "Gravity at the Quantum Level".*
The constant
ε0 can be written as 8.85 × 10-12/s2, but it can also be written as 2.95 x 10-20m/s2. Just divide through by c.
You will say the dimensions do not work, but they do, as you can see by going to that previous
paper.
At any rate, in "Gravity at the Quantum Level" , MM has found that same number for the gravity field of the proton. The constant is not the permittivity of free space, it is gravity as created by nucleons.
Of course this means that Maxwell's equation above is already unified. It contains the gravity field at that level, and is therefore another Unified Field Equation, UFE. Since Maxwell used the displacement current equation to modify Ampere's Circuital Law, we can say that Maxwell's equations are unified.
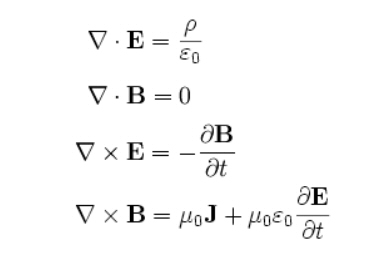
The displacement field equation is also proof of my real charge field, since—as defined by Maxwell— this field is not created by electrons or any other ions. Maxwell's displacement field pre-exists any field created by ions. In fact, if we study Maxwell's use of the displacement field, we find it creates the E/M field. The displacement current has dimensions of density, just as my charge field has, and if we go to Wikipedia, we find this:
The displacement current has an associated magnetic field just as actual currents do. However it is not an electric current of moving charges, but a time-varying electric field.
What does that mean? It means it exists whether or not you have any ions in the field. It is a sub-field to the Electromagnetic Field, and is not equivalent to it. As a matter of straight mechanics, it is the displacement field that creates Electromagnetism, not the reverse. Again, this matches my definition of the charge field. It is the charge field that is primary, and the E/M field that is secondary. Charge is photons, E/M is ions. The photons drive the ions, so they are the fundamental field.
So we already see that Maxwell's displacement field is simply another name for my charge field. And this explains—in yet another way—why the charge field has been undercover for about 150 years. In Maxwell's equations, it has been the electrical field and magnetic field that have gotten all the attention and fame, while the displacement field has been all but hidden. The displacement field has always been seen as little more than a mathematical manipulation, one used to push the equations in line with data. But almost no work has been done in a century and a half to explain the real workings of this displacement field. In fact, the mechanics of the displacement field is purposely hidden to this day, as we can see from this quote at Wikipedia:
"There is no free charge in such a material [a bar electret], but the inherent polarization gives rise to an electric field. If the wayward student were to assume the D field were entirely determined by the free charge, he or she would immediately conclude the electric field were zero in such a material, but this is patently not true. The electric field can be properly determined by using the above relation along with other boundary conditions on the polarization density yielding the bound charges, which will, in turn, yield the electric field."
That quote is completely catholic, and no current expert would likely disagree with it. But it is false nonetheless. See how the standard model explanation uses the word “inherent”? Compare that to their use of “intrinsic” in other places. In all places, these words are used to misdirect you away from real mechanics. They do not have any real mechanics, so they imply that any student who expects real mechanics at the quantum level is “wayward.” Another curious wording, wouldn't you say? Expecting physical explanations from physics is now wayward. Since current physicists cannot answer the questions of students at any level, they have to divert everyone into inherent and intrinsic properties. Another word for inherent and intrinsic properties is “unreal”, although they do not tell you that. To get their theories to work, they have to hide all real parameters at this level, telling you they do not exist. They then replace those parameters with virtual parameters. They can then manipulate these virtual parameters with their dense mathematical systems, forbidding you from asking mechanical questions. “You cannot ask mechanical questions about virtual particles or parameters!” Convenient for them, isn't it?
You see, the problem is they can't figure out how the charge in D is moving, so they just pretend it isn't. In their limited world, the charge is either moving or static. If it is moving, it is free, and they couldn't make that work. So it must be “bound.” But MM has shown the answer is neither free nor bound. The charge is moving, but it is not free. It is channeled . [See How Elements are Built - A Mechanical Explanation of the Periodic Table"] In the presence of ions, the charge field is channeled in defined vectors, which not only prevents dissolution of the ions and nuclei, but it also explains things like the magnets and electrets above. Moving charge sums to zero only in the case that it is free and unchanneled. But if it has a summed vector defined by charge channeling, then the qualities of magnets and electrets can be explained mechanically.
We see their confusion again when it comes to explaining capacitors:
"An example illustrating the need for the displacement current arises in connection with capacitors with no medium
between the plates."
No medium between the plates! It is 2013, over a century after Tesla, and we still have physicists telling us there is no medium between the plates! And you wonder why these guys end up with vacuum catastrophes and dark matter meltdowns. (See The Cosmological Constant is a fudge & Hubble Redshift is just curvature also the Vacuum Catastrophe.)
In the very next sentence, they say:
"The capacitor is in a circuit that transfers charge (on a wire external to the capacitor) from the left plate to the right
plate, charging the capacitor and increasing the electric field between its plates."
Wait, there is no medium between the plates, but there is an electric field ? So a field can exist with no medium? The field is nothing? Aren't these particle physicists the same guys that have “no force at a distance” on their t-shirts and gimme caps? If there is no medium, how is the field expressed between the plates? Don't tell me, let me guess: virtual photons. Mystical messages etched on the faces of ghost particles.
As you see, the displacement field has been covered over with dirt since the time of Maxwell. The charge field has become virtual! Current physics treats the displacement field as mathematical only, or as a theoretical convenience. But it does not work like any real field. (See Coulomb's equation is a Unified Field equation in disguise.)
Amazingly, modern theorists try to sell this fudge as a great advance:
"Few topics in modern physics have caused as much confusion and misunderstanding as that of displacement
current. This is in part due to the fact that Maxwell used a sea of molecular vortices in his derivation, while
modern textbooks operate on the basis that displacement current can exist in free space."
As you see, they are trying to convince you that the problem isn't that they have gone virtual and are not doing physics anymore. The problem is that silly old Maxwell was trying to explain this with mechanics. What kind of fool was he, a physicist trying to be physical?
In fact, we see that Maxwell was on the right track with his vortices, since we require real spins in the
displacement field, beneath the magnetic spins in the E/M field of ions. They are not “molecular” in
the way we understand molecules now, but they are vortices. Each photon can be thought of and act as
a tiny physical vortex, since each photon is spinning. This is what explains the displacement field, not
the current dive off into heuristic math. Wikipedia says,
"Clearly Maxwell was driving at magnetization even though the same introduction clearly talks about dielectric polarization."
But we now know it is neither. Maxwell wasn't driving at magnetization, nor was he driving at dielectric polarization. He was driving at real sub-magnetic polarization of real particles, which is what my charge photons give us. My charge field theory might be called either magnetization or dielectric polarization, but it is strictly neither. Why? Because both terms are currently used as descriptions of the E/M field, and my charge field is not a part of the E/M field. Although my spinning photons give us both polarization and a spin field (magnetic field), they do so via a sub-level of influence. Again, E/M applies to a field of ions. Charge applies to a field of photons, and photons are not ions. Since the photons drive the ions, the charge field is at a sub-level beneath the E/M field. The E/M field is only an outcome of the charge field. But because those in the mainstream misunderstood Maxwell's definitions and delineations, they have since conflated the two fields. Because they only have one field, they cannot describe the motions and forces they see in data.
We can also see the problem here:
Maxwell concluded, using Newton's equation for the speed of sound ( Lines of Force , Part III, equation 132), that
“light consists of transverse undulations in the same medium that is the cause of electric and magnetic
phenomena.”
You can see the conflation there, and the confusion. Whether the confusion is completely in the minds of those who came after Maxwell, or whether some of the confusion was his own, is not completely clear. But that quoted sentence is true only if you read it correctly. It has not been read correctly. It is true only if by “in the same medium”, Maxwell means in the same general space. (But the way it has been read historically is that light is undulations in the E/M field, but light is NOT undulations in the E/M field. Light is its own field. Furthermore, light is not undulations in anything. The wavelength of light is not a field undulation, it is a spin wave caused by each individual photon. Each photon has a wavelength, as we now know, and the only way it can have that is if the spin of the photon causes the wave. Light is a spin wave, not a field wave. (See Unifying the Photon with other Quanta, How they Travel, and why they go c.)
We have since discovered field waves in the charge field, but these waves are not photons and are not light. They are neutrinos. Neutrinos are Undulations in the Charge Field and thus not field influences of the E/M field.
Like everything else we have looked at, the mainstream has this one upside down. They think that light is moving in the E/M field. But it is actually ions that are moving in the light field. The charge field is primary, and it sets the ion field. Not the reverse. Light does not move in the E/M field. Light moves in the charge field, which is its own field. Light is charge and charge is light. Strictly, light does not move in any field. Light is the fundamental field. The motion of light sets all the fields in sizes above it.
In this way, charge field theory ties into Relativity, since Einstein basically proposed the same thing. In telling us that the motion of light determined the motion of everything else, Einstein was saying the same thing as MM. He never made the connection as explicit and clear as MM is making it here, but that is his most fundamental link to Maxwell. Just as Maxwell was (sometimes) trying to do, Einstein based everything on light. But now physicists have turned that on its head. They now try to define the motion of light relative to the E/M field. Since the E/M field is a creation of light, that can't work. They have cause and effect mixed up.
To fine tune your understanding of my charge field, we may go directly to Maxwell's paper of March, 1861 On Physical Lines of Force . Early in that paper, we find him explaining the magnetic field as a function of stress (p. 164).
"We must therefore represent the magnetic force at a point by a stress having a single axis of greatest or least pressure, and all the pressures at right angles to this axis equal. It may be objected that it is inconsistent to a represent a line of force, which is essentially dipolar, by an axis of stress which is necessarily isotropic; but we know that every phenomenon of action and reaction is isotropic in its results, because the effects of the force of the bodies between which it acts are equal and opposite, while the nature and origin of the force may be dipolar, as in the attraction between a north and a south pole."
Although Maxwell is fudging a bit here, it is refreshing it is to read a paragraph that is mostly logical and clear. One can understand exactly what Maxwell is saying on a first reading. It does not require translating a bunch of lingo and misdirection, trying to make sense of nonsense. But how is Maxwell fudging a bit? Well, he is trying to make you think it isn't really important that his stress is isotropic. Although he finds ways around it, it IS important, because it tells us he does not have a real understanding of his field. Because he does not understand that his field is being created by moving particles that have both linear motion and real spin—and that this spin can be either up or down —he does not start off with enough degrees of freedom to solve. He does not really need pressure or stress to solve magnetism, he just needs linear motion, real spin, and particle density. But because he does not see how to solve in the simplest manner, he solves in more complex manner, and is thereby forced into some greater or lesser pushes. We are seeing the first push here. If we start only with a line of force, there are NO pressures at right angles to that line. It does not really matter if we call the stress dipolar or isotropic: if it has “a single axis” it is thereby linear and not spherical. Since a single axis cannot be orthogonal to itself, we cannot talk of angles, right or otherwise.
You should see that my spinning photons solve this problem immediately, since every “point” in the field can be inhabited by a real photon, and that real particle already has potential forces at right angles to one another. Maxwell's problem here never comes up for me. In my field, every point is already sub-magnetic and sub-electric, since every single photon already has the motions that cause both fields.
Some will say that MM has already misunderstood Maxwell, because what he is really doing in this section is creating a state of stress symmetrical about an axis, but with variable stress down the axis. This makes his axis a sort of straight hose running z, with stress symmetrical only around each x,y, but not symmetrical down z. In this way, the hose can be squeezed like a tube of toothpaste, forcing the paste one way or the other. MM agrees that is what he has done, but he has already cheated. What he has proposed isn't a line of force or stress, and nothing here is either isotropic or dipolar. His stress in x,y is circular and centripetal, and his stress in z is linear; but his motion in z is dependent on variations along z in x,y. By making his explanation is too complex, this allows him to slip in things unanalyzed and undefined. To get this field of his to work, he will have to show a mechanical source for both these centripetal forces in x,y and their variations along z. To do this, he explains the x,y force as a sort of hydrostatic pressure and the z force as tension along the axis. But there are big problems with both.
The first problem is that hydrostatic force does not normally set itself up that way, as he has previously admitted in earlier paragraphs. Hydrostatic force is normally 3D. Only a limited hydrostatic force would act like that, as with our hose or tube of toothpaste. But no fundamental field would be expected to arrange itself circularly around selected axes. What determines if a point in the field is on an axis or in the pressure field around it? How does the field choose its own axes or lines?
The second problem is the z force, which is really only a reaction to the first force. But to get any reaction from the line, it can't be a line. It must be a tube. You cannot pressurize a point or a line. You can only pressurize a volume. In other words, the word “pressure” only makes sense with regard to real bodies that have real extension in 3D. Pressure applied to a point or line is meaningless and nonphysical.
This also means that Maxwell now needs some field inside his tube of influence that is not strictly equivalent to his field outside of it. He has two fields that are acting differently, so he must show us some difference. Why are one set of field particles inside the line and another outside? Why is one set pushing on the other in a circle? Maxwell has overcomplicated his fields and forces from the start. None of these problems come up for MM, because he understood that a homogeneous field was necessary at the foundation. Since the charge field is the fundamental field of the universe, it has to be easily universalized. A field of real spinning particles can be universalized. A field of pressurized tubes cannot. Maxwell has the same basic problem string theorists have, though on a lesser scale. He has created a small mess where they create a large one. And, we can see that string theorists got their ideas straight from Maxwell. His little tubes here are the obvious theoretical precursors to strings. If you read MM's paper Critique of String Theory: the inelegant universe, you will see that both fail in the same way.
We can see more similarities if we continue, for Maxwell next says,
" It appears therefore that the stress in the axis of a line of magnetic force is a tension, like that of a rope."
In string theory, precisely the same idea is used. But in both theories, the idea is very faulty. Maxwell's external stresses in x,y, varying along z, cannot create tension as in a rope. A rope is pulled from the ends, whereas his tube is being squeezed from the sides. His hydrostatic pressure is symmetrical around the axis, not to its ends. MM knows this because Maxwell says his hydrostatic pressures are at a right angle to his axis. If the pressure were coming from the ends of the axis—as with a hose being turned on at a faucet—then there would be no right angles. With a hose turned on like that or with a rope, we have equal tension or pressure along z. But with Maxwell's tube, we would have unequal pressure along z. It is precisely that unequal pressure that would cause motion along z, as with toothpaste. Either Maxwell misunderstands his own field, or he has described it very poorly.
Maxwell now tries to explain how a real field could create his lines of force. To do this he brings in his vortices. If we let these vortices be created by spinning spheres, we would let the poles align with his lines. His hydrostatic force is then caused directly by the centrifugal force of the eddies. In other words, the spheres spin, a centrifugal force is created at the equator of each photon, and this force is then transmitted sideways to Maxwell's line.
From this, you see how different Maxwell's theory is from that of MM, despite having a few external similarities. Maxwell needs his photons arranging themselves in little cylinders around his lines. But he has no explanation of what causes the lines in the first place. Why would photons arrange themselves in cylinders around lines? How big is each cylinder of photons or vortices? What determines the radius of each cylinder? Do you need only one vortex around each line, so that each cylinder is only one photon wide? Or not?
Notice how much simpler the explanation and field both are if we start with the photons instead of the lines. Let us say all our photons in a given field are aligned, with their poles all pointing the same direction (or summing to the same direction). Well, we already have Maxwell's field lines in that case, without further ado. Every photon becomes its own cylinder, and it affects its neighboring photon almost like Maxwell's vortices affect his lines. Except that we can simplify the mechanics even further. We do not need to propose that the photons affect one another across empty space by sending out eddies, and we do not need to propose centrifugal forces at the equators either. It is much simpler to propose that the photons collide equator to equator, you see, and transmit spin force by contact. That way we do not need force at a distance, we do not need a medium for the eddies, and we do not need centrifugal forces.
We also do not need photons existing side to side. Maxwell either needs a medium for his eddies or he needs a plenum, where his vortices are existing edge to edge. In either case he begs the paradox of Parmenides, where he has a block universe with no space and no room for motion. My field of photons does not hit that paradox, since real collisions do not require either a plenum or an intervening field. Nothing is stopping my photons from jostling side-to-side, moving a bit amongst themselves as they travel c. This jostling allows them to “communicate” by real collision, with no other medium, no eddies, and no plenum. Since the spins are real, angular momentum can be transferred in any collision. Collisions only require a real substance with a real boundary, which admittedly begs other questions. However, the questions begged are less vicious than the questions begged by a plenum, and they are questions not fatal to any physics. Physics assumes substance from the start—hence the name physics . Which is to say that in physics, the assumption of substance is never a contradiction or a paradox. It is not only allowed, it used to be required.
MM's theory is also preferable to that of Maxwell in that the photon forces do not work upon some dreamed-up field line. They work upon each other because these photons never interact with a field, they always interact with other photons or with ions. If we assign any pressure in the field, we do not assign it upon the field, but rather by one photon upon another photon or upon an ion. The field is never an active player in any of my theories. In the charge field, the photons are the field. We sum individual motions and collisions to find field potentials. Field potentials do not cause anything. Photon motions and spins cause field potentials, which then may cause greater motions by summation.
The question that arises is what causes the photons to align, as above? Maxwell proposes the field lines first, because he knows the photons need a reason to align. He probably thought it was a cheat to started with aligned vortices, just as you think it is a cheat to start as he did. But it isn't a cheat to given any matter, we will find the charge field channeled by that matter. As the photons are re-emitted by that matter, the charge field will naturally be aligned or one should say that if the photons are not aligned as a matter of spin or pole, there will be no magnetic field. If there is no magnetic field, we do not need to explain the genesis of it. If there is a magnetic field present, it will be caused by the spin alignment of the photons. And if the photons are spin-aligned, it will be because the matter present has aligned them. To find or create any magnetic field, we must have matter present, and we must have the right matter in the right state. It is the channeling of charge through matter that causes magnetic fields. Yes, each photon has a tiny magnetic field of its own, caused by its own spin. But that isn't enough to create a magnetic field we can measure.
This may appear to be a circular argument. If you say that photons create magnetism and now you tell us matter causes magnetism. It can't be both. You can't have photons causing matter to be magnetic and matter causing photons to be magnetic. Actually, you can, if you speak clearly enough. You need photons with spin to create magnetism, but photons with spin are not enough by themselves. If you have photons but no larger particles or objects, your photon spins are chaotic and do not sum to anything, not even locally. Nothing above the size of the photon will feel any magnetic effect. But if you can channel the charge through matter, you can create spin alignment and therefore a larger magnetic field.
This still leaves some unanswered questions: since you need matter in alignment before you can get charge in alignment, what caused the matter to align? If it is charge the it is the chicken or the egg problem. Even with no answer to the question of "What caused the first non-chaos in the charge field", MM's theory is better than Maxwell's and it is better than current theory. Neither Maxwell nor current theory can answer that question, but MM's theory is better because it does not require undefined stresses, tensions, field lines, or forces, it is a better theory and since it explains a lot of things mainstream theory has not been able to explain simply and mechanically. (More on this in the second section of this paper.)
Notice that Maxwell also avoids explaining why his vortices align with his lines, but he never gets around to addressing it, as MM has just did. Because his explanation is denser, you forget to ask the question. It is precisely because my explanations are so short and concise that readers see so many questions. I have to answer far more questions than the mainstream, and that is why. Most readers can't even penetrate what the mainstream is saying, so questions do not arise. Of course the mainstream does that on purpose. Theories are put into dense math and lingo expressly to prevent questions.
After studying Maxwell's paper closely, MM could see his original fault. He has not been misunderstood or misinterpreted. There has been no misreading, there has simply been a failure to correct him. The central problem here is that he thought and proposed that light was a wave in the E/M field. So he had it upside down from the start. Since electricity and magnetism were discovered before charge and were far easier to study, Maxwell naturally took them as primary. Electromagnetism is the motion of ions, while charge is the motion of photons. Since photons are very much smaller than ions, they hadn't been studied in Maxwell's time. We still know almost nothing about them. For this reason, Maxwell took the E/M field as the foundational field, and tried to fit light into it, explaining light as a field wave in the E/M field. But this is upside down. Light does not move in the E/M field, ions move in the light field. The motions and spin of photons create everything, including ionization, magnetism, current, and so on. The charge field is the fundamental field, and the E/M field is only a creation of it. This one reversal explains most of the confusion that still exists.
Next MM continues to study Maxwell's exposition of his displacement field, which is equivalent in most ways to MM's charge field. MM will show how Maxwell's vortices fail, how to correct them, and how to calculate the charge field straight from the Electrical Field.
In part 2 of his paper of 1861 entitled On Physical Lines of Force, Maxwell returns to the vortices he proposed in part 1. We will find he quickly makes a mess of the whole problem, which is why he very soon had to dump the whole idea. His failure has been a 15-decade tragedy, since the failure of a top theorist and mathematician like Maxwell convinced everyone the problem was either insoluble, or at least insoluble with any sort of spin mechanics. No one after Maxwell tried to fine tune his solution, to make it actually work, although it is that hard to do. This may be why physicists following Maxwell in the late 19th and 20th centuries were so afraid of being wrong. Feynman was still deathly afraid of publishing something that wasn't right in the 1980's (although MM has shown he did so anyway).
Maxwell's failure to explain electromagnetism mechanically in the 1860's basically scared physicists for seven generations, including Maxwell himself. Chastened by his failure, Maxwell all but swore off mechanical proposals and, like his colleagues, hid more and more in the math. And so he set a precedent that has stood to our own time. As a subfield of physics, mechanics took a steep fall in the 1860's, then took another steep fall in the 1920's, with the Copenhagen interpretation. Physics has never been the same since. Not only has it not recovered, but its fall has accelerated with each passing decade.
(See Addendum to Critique of String Theory: the inelegant universe as to how the early string theorists borrowed Maxwell's failed lines of and renamed the lines “strings,” and then jettisoned the vortices, but kept the tension along the line, which became the tension on the string.)
We see Maxwell's first crash-and-burn on page 283 [just before eq. 27]. He sees that he needs all his vortices spinning the same way, so he is forced to propose a row of idle wheels in between each row of vortices. This is what MM meant earlier, when he said Maxwell was falling into the paradox of the plenum. He not only has vortices, he has them existing cog to cog. He is trying to create a pinwheel universe, and we see why he was later mocked for it. In this section, we see him proposing a universe not far different than the Aristotelian orrery universe, and it does look a bit ridiculous. He spends dozens of pages of equations calculating the motions of these idle wheels, which is sad. MM admires Maxwell for attempting a mechanical explanation, but wishes he had done it better. Still, we all make mistakes, and the real tragedy is not Maxwell's error here, it is that the error hasn't been corrected in 150 years. Maxwell's greatest error here wasn't this limited mistake, it was giving up and letting others convince him to abandon mechanics.
Of course, the same sort of people that gave Maxwell a hard time for his attempt at mechanics are still around today, critiquing MM. These types do not even bother to read his papers closely. They skim a few pages, just enough to discover he is trying to apply spin mechanics to the charge field, which is enough for a knee-jerk dismissal. Maxwell failed, so must MM surely fail, too. Everyone from Kelvin to Bohr to Feynman has assured them of that. They have been taught that all mechanical solutions at the quantum level must fail. This is RULE 1 of the Copenhagen interpretation. All top physicists have been mocking mechanics for decades. Mocking mechanics is the go-to pose of contemporary physicists, and it is taught day-one in graduate school. Big math is cool, mechanics is uncool.
Although Maxwell made a mess of spin mechanics here, his mess can be cleaned up very quickly and easily, which makes it very difficult to explain why no one has done that cleaning in 150 years. Maxwell does not seem to realize that he does not need his vortices spinning one another. He can take the spin as given, and what he really needs to explain is why the jostling does not totally de-spin them. Even that isn't difficult. The jostling does de-spin them, which is why a magnetic field dissipates over very long distances (in some circumstances). But these are photons traveling c, and any field we are studying on Earth is fairly short. In crossing the field, there isn't enough jostling to de-spin the field to any measurable extent. Whatever spin the photons had at one end of the field, they will still have at the other end. So there is nothing to explain.
The same goes for the original spin. Maxwell does not understand why he can be given the spin, because he does not understand his field mechanics. He does not understand that any magnetic field he could be studying or proposing must have been created by charge passing through matter. It is the matter that sorts the spins, or makes them coherent. It is the coherence that explains the strength of the magnetic field. The matter does not have to spin the photons, since they are already spinning. It only has to sort the spins. Some matter does this well and some does not, but if Maxwell is giving himself a magnetic field, he is also giving himself some amount of matter capable of sorting the charge. So he is given the spin coherence. He does not need to have the photons spinning one another all along the path.
The same goes for the original spin. Matter does not spin photons, it only coheres the spin by channeling it. So where does the original spin come from? Simply from collisions. If you have no baryonic matter in an area, you would have no spin coherence and no magnetism, but you would have spin. Why? Edge hits. Any edge hit will cause spin. So we do not really have to explain spin, either. Notice that, given a lot of tiny spheres flying around randomly, it is much harder to explain lack of spin than spin. Say you were given a universe of spheres colliding randomly. Then you were told they were all not spinning. That would be the mystery, would it not? Spin is no mystery. Lack of spin would be the mystery to be explained. The only way you could explain lack of spin is if the spheres never collided. But the probability of that is zero. Therefore, spin is the default state. And the amount of spin we find is simply a function of the density of our spheres.
You will say, “No, in a random collision of spheres, the spins would sum to zero. There should be no spin.” No, that is only true globally. If we start with spheres not spinning, then let time pass, after any time the total spin is zero. That is true. But the total spin applies to the entire set, not to any subset. Therefore, in any space smaller than the entire space, the spins would not sum to zero. Therefore, spin is given.
This only leaves us with c. Why are photons going c? (See "Unifying the Photon with other Quanta, How they Travel and why they go c".) Doesn't that break the conservation of energy law? No, it does not, since energy is conserved in a system . A fundamental field isn't a system. To conserve energy, we only have to have the same total speed in our field at time x as we have at time y. We do not have to have zero speed. Again, the easy way to see this is to follow the previous logic. All photons at speed zero would actually be harder to explain than all photons at speed x. The only way to explain all photons at speed zero is to propose no motion and no collisions. Any motion in the field will eventually translate through the entire field via collisions, so velocity is the default state. Statistics tells us the same thing. There is only one way to have all photons at speed zero, and an infinite number of ways to have them not at speed zero. Therefore, the probability of speed zero approaches zero and the probability of speed x approaches 1. The actual speed is then determined by the density of the photons and the initial relative motion.
Now let us return to Maxwell's displacement field equation:
D = ε0E + P
First, let us write that in terms of the Electrical Field E:
E = (D – P)/ε0
The electromagnetic field depends on the charge field. The charge
field is primary and fundamental, and the E/M field is only a result of it. One might have been asked how
the two fields relate mathematically, and now we see how they do. Since MM showed you that D is really
my charge field and that ε0 is really the gravity field at the quantum level, we can rewrite the equation this way:
E = (C – P)/g
To really make sense of this, we also have to re-define the variable P, which current theory gives to
polarization density. What are they really trying to represent with that, as a matter of mechanics? To
understand it, we should ask what the equation would lack without it, given my mechanics. What if we
only had this equation:
E = C/g
That would represent for me that the Electrical field was equal to the Charge field divided by the local gravity field. What is missing there? The matter field. Given just those three variables, we do not know how much matter is present, or in what form. Since it is the matter that is making the charge field coherent as a matter of spin or focused as a matter of charge strength, we need to know that. Since we have no magnetic component here, we can ditch the spin coherence consideration in this particular equation, but we still need to know what matter is present to know how charge is coming out of the nucleus. In How Elements are Built - A Mechanical Explanation of the Periodic Table", we have seen how different elements channel charge in different ways —at different densities. This is what the variable P is really telling us. They claim it is telling us the amount of charge separation, but that is wrong. We do not need charge separation, and they actually know that. They know that in quantum experiments, we can get high values for P without charge separation. Near the nucleus, we get channels of high charge densities without having free electrons nearby to create this naïve charge separation.
They try to fudge this charge separation by telling us that the atom's own electrons create this charge separation, but since the measured charge channels extend beyond the proposed electron orbitals, this explanation does not wash. It especially does not wash now that MM has shown there are no electron orbitals. The electrons are orbiting only in eddies around the proton poles, not around the nucleus as a whole, so the charge separation idea is blown. Polarization density is simply a density, and it has nothing to do with polarization in this way. We need the variable P in the above equation simply because we need to know what elements are present, and how they are channeling charge. This variable tells us that.
Therefore, we need to tweak the equation a bit more. Given my variable re-assignments, the minus
sign no longer makes sense. In this equation, we now see that C must be the ambient charge field
density, and P is the charge field density as it is emitted from the matter present. We then add them
together to get the total charge density at a given point outside the nucleus. So the equation should be,
E = (CA + CN )/g
That is, ambient charge and nuclear charge. However, since you would have to leave the atmosphere of the Earth to get a good measurement of the ambient field, this equation is not of much use in that form. In Maxwell's time there would be no way to get a value for it. Now, we could get a value for it, but we do not. We do not choose to write the equation in that way or in that direction, because we haven't understood there IS an ambient field. Therefore, we would have to solve in the other direction, measuring E and then solving down for the two C terms.
This equation now gives us a way to calculate the charge emitted
by various elements and molecules. Up to now we could only measure the electrical field E, not the
charge field C. We still can't measure the charge field directly, but with this new equation we can
calculate it. Like this:
Eε0 – CA = CN
We can measure E directly, we know ε0, and we can measure CA from satellites. You will say, “Won't we always be measuring E, even with satellites out in space?” Yes, strictly, that is true. To measure CA , we would have to measure the field with no ions in it, and if there are no ions, we have no way to measure. Our machines can only track ions, not photons. However, we can get around this by extrapolating. All you have to do is measure E near the surface of the Earth, then in the upper atmosphere, then in space near the Earth. You will find falling values of E, of course. You then calculate the limit of those values, which should be a value above zero. That value should be a good estimate of CA . Using the equation above, that will give you a value for CN . Just a suggestion. It may or may not be feasible, it has to be tried. This new equation proves by itself that the charge field is not virtual and that charge is not mediated by virtual or messenger photons. Since we will obtain a real value above zero for both charges, the charge field must be real. Virtual fields do not give us real field values. We only needed virtual fields because we could not calculate real fields, but now we can.
Of course, it is not MM's new equation that proves this. Maxwell's displacement field was proof enough that the charge field was not virtual. His equation—without MM's updates—is a real field equation that yields real values, so it is hard to understand why physicists now think they can mediate the charge field with virtual photons. How can they bury the charge field under virtual gymnastics when their own master Maxwell has given them a real equation for the field? The only answer to that is that they have never recognized what this displacement field really is. Because Maxwell's vortex theory failed and was dumped, they have also dumped the mechanics of the displacement field. Since Maxwell couldn't provide a mechanics for it, they have kept it but made it non-mechanical.
You should find that very curious. Their reasoning apparently goes something like this: Maxwell showed us a field that works in the equations. It is clearly necessary. But he failed to show us the mechanics of this field. Therefore the field is non-mechanical. You can see the illogic there. Maxwell's failure to show the mechanics was no indication that the field was non-mechanical. It was only indication that he couldn't figure it out. The logical thing to do would have been to continue to seek the correct mechanics. The reaction to Maxwell's failure was unscientific in itself. That unscientific reaction has persisted for 150 years now, to disastrous effects.
This finding is important because it explains the current confusion about the charge field. If we seek just one main reason that contemporary physics is so gloriously ignorant of the charge field, it is this. Maxwell's failure to explain the mechanics of the displacement field in 1861 buried field at that time, and it has been buried since. It was immediately pushed into the background, and has existed in the dark all these generations. Now, physicists do not even understand that the displacement field is linked to charge. For modern physicists, the displacement field is just a mathematical nicety, a minor feature of the Maxwell equations, one hardly worth talking about or teaching. In fact, because it is not understood, they have preferred to hide it. It is often not taught at all, and when it is taught it is taught in cloaking terms. If you ask any questions about it, you are “wayward.” As for the charge field, modern physicists do not believe in a charge field . They see no link between the displacement field and the charge field, so they have to bring in virtual photons to explain charge interaction at the quantum level.
And so digging out of the displacement field is of paramount importance. MM has proved that it is
not only equivalent to the charge field, it is primary. The charge field sets the E/M field, by the
equation above, so charge is the foundational field. The unified field is not composed of gravity and
E/M. E/M is only result of charge, so the unified field is properly expressed as a composition of
gravity and charge . This is why MM has written his unified field equations as a unification of charge,
not E/M. As we now see, the E/M field is already unified . Just consult the equation above:
E = C/g
That is already a unified field equation, and we can see the unification in the equation. The Electrical Field is Charge over Gravity. The ratio indicates the unification.
To read more about this see Gauss' Electrical and Gravity Law are Unified Field Equations using about four lines of simple math.
*This is not to be confused with quantum gravity, since by “quantum gravity,” the mainstream currently means quantized gravity, not gravity at the quantum level. MM is not only showing how gravity is unified with charge, he is showing how the old equations were already unified. In other words, we do not have to unify the math we have. It is already unified, and we simply have to see where it contains gravity.