Gauss' Electrical and Gravity Law are Unified Field Equations
© Miles Mathis
First published May 7, 2013 Having proved Maxwell's equations are disguised Unified Field equations"
showing in the shortest form of the unified field equation that In the equation:
MM's C equals the current Q, since both stand for charge. And this previous paper ε0
it is show to actually be Gravity at the Quantum Level. This paper will now make this connection
explicit, as well as to expand on what this unification means for Gauss' Law.
E = C/g shows the unification of the two fields: gravity and charge
To start with, you can see mathematical proof above: E = C/g. E is the ratio of two
fields, C and g. One way to unify two variables is to put them in a ratio. Two variables: one term:
hence, unification. Two become one: that is what “unify” means.
In Coulomb's equation is a Unified Field equation in disguise it was shown that, since Coulomb's equation is an E/M field equation, the E/M field must be
unified. The gravity field is unified with the charge field, but there is difference between charge and electricity. The E/M field contains gravity, so the field is already unified, so there is no need to unify E/M with gravity.
In Newton's law is a Unified Field of Gravity and E/M, Newton's equation gives us the celestial field, normally at a larger level of size.
Newton's equation has always been assigned to the gravity field, but it really is a unified field of gravity and charge.
Now in respect to Gauss' equation, it will be shown that it is also a unified field equation. This is simple enough, because
all that has to be shown is that the variable we now assign to permittivity or the electric constant, ε0, is
really gravity at the quantum level. It is mainly the gravity of the proton.
But some will still have questions. The most sensible question would be this one, “If the Electrical
field E is unified, and includes both charge and gravity, why is this unification represented by a ratio?
Why not a product? Why not ΦE= Qε0? Wouldn't a product be the more natural expression of unification?”
Well, if the mechanics were other than they are, that might be so. If, for instance, the two fields were
stacked, with one field existing right on top of the other, then we would expect a product, but that is
not the mechanics we have. As it happens—and as we can see by simply studying the real interactions
—the fields are not stacked. We do not have charge existing on top of gravity. We do not have a
situation that would logically call for integration or multiplication of fields. What we have physically
is a charge field that is operating inside of the gravity field. We do “integrate” the charge field into the gravity field, by one meaning of the word “integrate.” We put it in there, which is one meaning of
integrate. So some would jump to the conclusion that we should “integrate” with our math as well. To
integrate would imply multiplication, not division. The reason we do not do this is because charge is
determined by the real motion of real photons, and like everything else, these photons are moving
inside the gravity field.
Inserting one field into
another could either give us a product or a ratio. Just because the photons are moving inside the gravity
field doesn't automatically give us a ratio. We need to look even closer. We need to look at
how the photons are moving in the gravity field. In almost all situations, the photons will be moving
as a summed vector against the gravity field vector. In both Newton's equation and Coulomb's
equation (and in the Lagrangian and Maxwell's equation) charge is moving as a vector against the
gravity vector. So, depending on the form of our math, this should either give us a differential
(subtraction) or a ratio. If we are calculating single events, or single positions of individual objects, we
will often use subtraction, as MM has in many of his papers. If we are combining entire fields to get a
flux or something like that, we will use a ratio, as here.
So why does the charge vector normally sum opposite to the gravity vector? Photons are actually recycled through matter.
They are recycled through the bodies of protons, neutrons, electrons, mesons, and so on. In this
recycling, they must go both in and out, so at various times in the cycle they are moving both in and
out. This would mean they are moving both with and against gravity, depending on where you measure
them. Gravity always points in toward the center of any real object, and if photons are being recycled,
they are moving both in and out. But in almost all cases, what we call charge is the photons going out,
not the photons going in. This is because the greatest results of charge normally happen near the
nucleus or proton. Matter tends to take a chaotic and undirectionalized ambient charge field and focus
it.
To see how this works, it is easier to look at the Sun. The Sun focuses the charge field just like smaller
bodies, but it is easier for most people to visual the Sun doing things than to visualize protons doing
things. If you take a sphere like the Sun, you will find it spinning in one direction only. It is possible
that it is made up of smaller bodies spinning randomly, but as a whole it can have only one spin. Or, its
outer surface can have only one spin. The outer surface cannot spin x and -x at the same time. Nor can
it spin x and y at the same time. If the body is any sort of solid, it has one and only one main spin on
its outer surface. This is what we find with the Sun and galaxy and Earth and so on. It is both logical
and it is all data. The Sun is spinning to the left, but it is not also spinning to the right. Therefore, if it
recycles charge using this spin, it must tend to focus or directionalize that charge. Say that charge is
coming into the Sun from the galaxy from all directions. The ambient field is more or less random.
But if the spin of the Sun causes it to pull in photons at the poles and emit more at the equator—as I
have shown—then the emitted charge field of the Sun will be more ordered than the ambient field.
And again, this is what we see. The emitted charge field of the Sun is emitted most heavily in a disk,
which travels out in the Solar plane. It is this plane where the planets exist.
Well, protons and nuclei work the same way. They give more order to a less ordered charge field. The
charge emitted from the nucleus is both more focused and more ordered than the charge coming in.
Because it is more focused and more ordered, it has more power to cause things to happen. A
disordered charge field cannot drive ions, because the ions are hit from all directions. They do not move.
But an ordered charge field causes motion. The ions are hit from one direction instead of many, and
they move. The movement of ions is what we call the E/M field.
For this reason, the charge coming out of the nucleus is more important than the charge going in. It is
the charge going out that defines the E/M field, so it this charge that we are normally concerned with in
our equations. Since this charge is going out, and gravity is pointing in, the two fields will normally be
in vector opposition.
That said, we must always be aware of the mechanics, because
even this rule is broken as as MM has shown. We have to follow our photons like wind or a vector potential, since in a few
special and limited cases charge and gravity will not be moving in opposite directions. If we are near
the proton pole or nuclear pole, we may be monitoring photons going in. If we are inside the nucleus
add. This will also be the case in some situations near the Earth's pole, the Sun's pole, or the galactic
pole, and you have seen me add field vectors in previous papers. There is no blanket rule of math,
there is only mechanics, and you must be aware of the actual mechanics in each problem, and in each
line of each problem.
This can be accomplished in about four lines of simple math, by making one simple substitution, thus unifying gravity and E/M in the most direct manner possible. First published May 8, 2013
Please note that this paper is a simplification by me of a paper or papers written and copyrighted by Miles Mathis on his site. I have replaced "I" and "my" with "MM" to show that he is talking. All links within the papers, not yet simplified, are linked directly to the Miles Mathis site and will appear in another tab. (It will be clear which of these are Miles Mathis originals because they will be still contain "I" and "my".) The original papers on his site are the ultimate and correct source. All contributions to his papers and ordering of his books should be made on his site.
(This paper incorporates Miles Mathis' gauss paper and
gauss2 paper.)
Gauss
E = C/g
Miles Mathis will show that this is just another way to write Gauss' Law
ΦE = Q/ε0
Some may find that statement to be esoteric or mystical, therefore exactly how
does this ratio show the unification?
How to go from Gauss' Electrical Law to Gauss' Gravity Law
Since it has been shown above that Gauss' electrical law is a unified field equation and so is Newton's gravity equation, we should be able to go from one to the other directly. No one has ever tried to do that, because one is thought to be an E/M field equation and the other is thought to be a gravitational field equation. However, since they are both unified, we should be able to go directly from one to the other. This can be done in the simplest manner.
The key to this jump will be the constant ε0, which MM has shown actually to be Gravity at the Quantum Level. Historically it has been unassigned or misassigned, which has made what MM is about to do impossible until now. It has been called the electrical constant or the permittivity of free space, but neither assignment has been correct. It is easy to see that neither definition has any mechanical content. As the electrical constant, it is admittedly not assigned to anything specific. And as the permittivity of free space, it is assigned to something that cannot logically accept it. You cannot assign a real number to free space, because if you do that space is no longer either free or space. Also in Coulomb's equation is a Unified Field equation in disguise and Maxwell's equations are disguised Unified Field equations MM derived gravity at the quantum level by independent methods, finding the constant ε0 both times.
However we cannot just substitute ε0 for g directly, since the dimensions do not match. Fortunately, it has
already been shown how to make the substitution , and it is very simple. We just divide by c:
g = ε0/c
Our next step will be to show that Gauss' law for the electric field is equivalent to Gauss' law for
gravity. To see this most easily, we will start from the spherical electrical field equations of Gauss:
E = Q/4πR2ε0
E = Q/4πR2gc
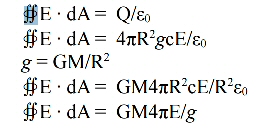
Now, to transfer from that unified field to the “gravitational” unified field, all you have to do is transfer
one surface integral to the other. Since we are going from E to g, we just multiply through by g/E
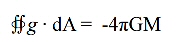
That is Gauss' gravity equation. So I have just proved that the two equations are equivalent. They are just written in different symbols. This is new information, and extremely important, because although current theory knows that Gauss' electrical law can be connected to Coulomb's equation, and that Gauss' law for gravity can be connected to Newton's equation, it doesn't know that Gauss' two laws are equivalent as unified fields. It couldn't know that, because it has never seen that the electrical constant ε0 is really a representation of the gravity field at the quantum level. Without that bit of information, one could not possibly do the math here.
Since it is known that Gauss' gravity equation is equivalent to Newton's gravity equation, MM has just linked up Newton's equation with Maxwell's equations. (See Newton's law is a Unified Field of Gravity and E/M and Maxwell's equations are disguised Unified Field equations.) MM has shown how to go directly from one to the other. Since Gauss' electrical equation is known to be equivalent to Coulomb's equation (see Coulomb's equation is a Unified Field equation in disguise), MM has also linked up Coulomb's equation with Newton's equation, meaning that one can go from one to the other directly, with straight variable substitutions. This what science has been trying to do for centuries!
Let us examine the implications of this relationship. For starters it means that all the attempts at unification by exotic and complex methods can stop as MM has given the solution. The mainstream was missing some very important pieces of the puzzle, so they have long been under the impression that unification must be difficult. It has certainly taken MM several years, and a lot of housecleaning, so it was not easy, but once done, we can see that the math is absurdly simple.
In addition, it means that we have even more proof MM's nuclear theory is correct, since if we have gravity at the quantum level—existing all along in Maxwell's equations—we have to take another look at the strong force. Current theory has proceeded all along with the assumption that gravity is absent or negligible at the quantum level, but it isn't. Even without my nuclear diagrams in How Elements are Built - A Mechanical Explanation of the Periodic Table, it is clear that all strong theory would have to be redone from the ground up. Fortunately, I have already done most of the hard work there, too, and I have replaced the strong force with charge channeling. (See papers on the strong force.)