Miles Mathis: Tides are caused by E/M field not Gravity

Please note that this paper is a simplification by me of a paper or papers written and copyrighted by Miles Mathis on his site. MM have replaced "I" and "my" with "MM" to show that he is talking. All links within the papers, not yet simplified, are linked directly to the Miles Mathis site and will appear in another tab. (It will be clear which of these are Miles Mathis originals because they will be still contain "I" and "my".) The original papers on his site are the ultimate and correct source. All contributions to his papers and ordering of his books should be made on his site.
(This paper incorporates Miles Mathis' tide paper, tide2 paper, tide6 paper, tide4 paper, tide5 paper).

Introduction

First paper on tides posted October 7, 2005

This paper starts with an extensive analysis of current and past tidal theory to prove that these theories fail. These theories are ingenious in many ways, since they find many clever methods for forcing a solution in a field that cannot possibly yield one. For example in the standard model, we are told that, although the Sun's field is stronger than the Moon's, its differential field changes less quickly, and this differential field is the one that causes tides. This is ingenious, but false. All the math done by the standard model is completely wrong from top to bottom.

It will be shown incontrovertibly that every trick that has been used, including the barycenter trick, "does not hold water." (excuse the pun) No tidal theory has ever been successful at deriving the tides that we experience, in spite of the existence of tide tables. Current tidal theory exists only by subterfuge. Once one points out all the fudges, it crumbles into a ugly pile of very dishonest math. Thus tidal theory remains to be one of the biggest messes in contemporary physics.

Clearly, we know that our ocean tides are caused by the Moon, since they follow lunar cycles. Although the mechanism has remained mysterious for centuries or millennia, it was always clear that the Moon was the overriding cause. In fact there are many other cycles that follow the lunar cycle, and these have remained just as mysterious. There are myriad animal and plant cycles that follow the Moon.^1* All of these monthly cycles, like tides, are assumed to be caused by gravity.

Certainly it is easy to imagine that terrestrial tides are caused by gravity, but why would other monthly cycles like the human menstrual cycle be caused by gravity? One might start believing that it is caused by astrology or 'gravitons'. Since these theoretical 'gravitons' have not been discovered yet, it is safe to say that they are just as unscientific as astrology. Without a physical mechanism, we are dealing with magic, no matter how much up-to-date jargon we use.

It s not far fetched to say that he Moon's E/M field affects the menstrual cycle, since we have ample proof of the electric and magnetic field and its direct effect on the human body. We already know that the brain and nervous system work in large part on electrical impulses. The body, like the oceans, is mostly saltwater: therefore it is a lovely conductor. What is more, we have a simple way of expressing the mechanism of the E/M field, which is photon bombardment. Since the standard model of tides is flawed, then, by extension, it is much more likely that tides are also caused by E/M field rather than gravity.

Miles Mathis has shown that the gravitational field is an acceleration field which creates a pseudo-force field, but this pseudo-field cannot fluctuate in the way we have thought it could. All possible fluctuations of this sort must be given to the E/M field. In Newton's law is a Unified Field of Gravity and E/M MM splits Newton's equation into a gravitation part and an electromagnetic part. What we now call the gravitational field is actually a differential field made up of both the gravitational pseudo-field and the E/M field, thus all fluctuations belong to the E/M component; none to the gravitational component.

Analysis of the Failure of the Modern Standard Theory of Tides

Let us compare the Sun’s field to the Moon’s field, at the Earth:

Force on the Earth by the Sun:
a_S = GM_S/r² = .006 m/s²
Force on the Earth by the Moon:
a_M = GM_M/r² = .000033 m/s²

You can see that the Sun has a much stronger gravitational effect on the Earth, if we look strictly at field strength. We already know this because, if the Moon had a stronger gravitational effect, we would be orbiting it, not the Sun. By the math above, Sun tides would be about 180 times as great as Moon tides, making the Moon tides invisible. Our tides would follow the movements of the Sun overhead!

The reason that we are not experiencing Sun tides that are stronger than Moon tides is according to the Standard Model is that, although gravitational forces follow the inverse square law (force is inversely proportional to the square of the distance), the tidal forces are inversely proportional to the cube of the distance. Thus although the Sun's gravitational pull on Earth is 179 times bigger than the Moon's, but because of its much greater distance, the Sun's tidal effect is smaller than the Moon's (about 46% as strong):

F_S = GmM_S/r3
= 2.4 x 10¹¹ N
F_M = GmM_M/r3
= 5.1 x 10¹¹ N

These equations, as MM has simplified them here, don’t give the right numbers, but we do get 46%. How was this "inverse cube law" derived" is pretty much by phony math. (For more details on this, see MM's website The Trouble with Tides for a more in depth discussion.)

The Standard Model, or its upper levels, appears to be currently founded on the inverse cube "law," but it is inconsistently applied. It is applied in conjunction with the centrifugal effects in regard to tidal effects on the Moon, but not when explaining tides on the Earth caused by Sun and Moon. This is because the current model needs to keep the Sun’s effects low, so that they do not conflict with data. The math is fudged to get to the 45%, that it really results in 67% which is just too high

Regarding the barycenter answer, it has not been accepted even though Feynman liked it. To disregard Feynman, physics has to have a pretty good reason, and MM has shown you the reason. If we apply the correct math to the barycenter theory, then we find that if it is true it swamps everything. It gives us two high tides that vary 1/1.22, which we could readily accept. Except that these tides are so huge that all the other variations are lost. The neap tides and spring tides are easily measurable: the data can’t be explained if the effect from the Sun is 72 times smaller than the main effect. Lunar perigee and apogee variations also would become negligible if they were compared to a barycenter tide. All effects from variation in the lunar orbit would be lost.

All this is a terrible problem. If you accept the postulates of current gravitational theory, then you are led inexorably to the barycenter tide. But you cannot accept it because it conflicts strongly with all data. It cannot be absorbed by even the most creative theory or math. But if you throw out the barycenter tide, then you have to throw out all the bath water too. We used the same physics and the same differential equations to find the barycenter numbers that we did to find the Solar and Lunar numbers. If the physics and equations are wrong, they must be wrong all the way down. We cannot just go back halfway, taking the numbers we like. We have to throw out all the numbers and start over. Even more, we have to throw out all the assumptions. No matter how we followed the assumptions, we arrived at numbers that did not work. This is called a failed theory.

Ask yourself why Feynman didn't insist on the barycenter solution. He was in a position to insist, and he was the type to insist if he knew he was right. He did not insist because it was only a suggestion, one he could not ultimately make fit the data. He saw correctly that it was the logical answer given gravity, but once it did not fit the data, he gave it up. He was always an empiricist, and never let his theory get before the facts. Now, ask yourself why Feynman did not follow up with another theory. Surely he could see that gravity insisted on the barycenter tide. If the barycenter tide does not work, then there is something seriously wrong with gravity. The only way the barycenter tide could be false is if it is itself being swamped by another force field. What could this field be? Feynman obviously did not have a clue.

Tidal theory, like so much other contemporary theory, has become a farce. Newton proposed the Moon’s gravitational field as the cause of tides and no one has seen fit to correct him, even though we have data now that makes his theory ridiculous to keep. If Newton had known a mass and distance for the Sun and Moon, he would never have proposed the theory he did (one hopes).

Now, MM admits that tidal theory has become very advanced in some ways. New models can predict the effects of tides with greater accuracy. And tidal theory is quite successful in showing how the given forces can create the tides we see. But it has made no progress since Newton in explaining the genesis of the fields themselves. As MM has shown here, the foundational theory of tides is little more than a bad joke. The Standard Model tries to keep all this out of sight, and it is amazingly successful in doing so. Most tidal analysis does not mention the relative strengths of the fields of the Sun and Moon, since it immediately explodes the theory. Only places like Wikipedia are foolish enough to hang the dirty laundry in the open air. Most books and websites are long on computer graphics, historical glosses, and advanced mathematics, and very short on foundational theory. We can now see why.

Tidal Effects on the Moon

Now let us look at tides on the Moon. The Standard Model, as glossed in textbooks at all levels, explains tides by showing that real bodies do not behave like point particles. Because they have real extension, different parts of the body must be feeling different forces. If we take the Moon as an example, we can compare three points on or in the Moon. We take the point nearest the Earth, the point at the center of the Moon, and the point farthest away. The point at the center feels a force from the Earth that is just sufficient to make it orbit. That is why, in fact, it is orbiting. It feels no tides of any kind. The point nearest the Earth requires less force to make it orbit than the point at the center, but it actually feels more force. The point farthest from the Earth requires more force to make it orbit, but it is feeling less force than the point at the center. The point nearest therefore feels a resultant force toward the Earth and the point furthest feels a resultant force away from the Earth. This causes a tide that maximizes at the near and far points.

So far so good. The Standard Model applied to the Moon follows what we have already found regarding the Earth. But before we analyze it again, let’s look at something interesting. Notice how theorists who claim to believe in General Relativity always revert to Newton when it comes time to explain forces in gravitational fields. In the chapters on General Relativity, we are told that an orbiting body is feeling no forces. It is simply following curved space, the “line” of least resistance. We are shown the ball-bearing on the piece of rubber, and the tiny marble orbiting it with no centripetal force. All quite ingenious, except that it does not explain the genesis of the forces at a distance used in tidal theory. How can an orbiter that is feeling no forces achieve tides? Even more to the point, how can an orbiter that is traveling in the curved space of its primary re-curve that space in order to transmit a tidal force to the primary? Is the gravitational field between the Moon and Earth curving convex or concave, relative to the Moon? MM would think it must be one or the other. It cannot be curving both ways at once.

The gravitons conjecture would throw out the curved space idea as superfluous. If we have gravitons mediating the force, then the Moon is feeling a force. In which case we don’t need curvature to explain anything.

But the current theory is not even that advanced, regarding tides. Graviton or no graviton, the theory reverts to Newton for the explanation. To cover all its bases, the theory gives the situation a sort of double cause. The first cause is given to the gravitational field. Nearer parts of the body will accelerate toward the Earth faster than farther parts, regardless of their weight or mass. Remember that acceleration in a gravitational field has nothing to do with mass. All objects fall at the same rate. Acceleration is dependent only on radius. So the analysis should always be talking about accelerations, not forces. This part of the theory is at least logical, given Newton’s equations. It is true that the static gravitational field would create tides as claimed, near and far. But it would create these tides even if there were no circular motion and no orbit. An object in free fall would experience this sort of tide, as the Standard Model admits.

Current theory gives a second mechanism, and this mechanism requires an orbital velocity. Nearer parts of the Moon orbit in a slightly smaller circumference than farther parts. They travel this circumference in the same time as the rest of the Moon. Therefore they have a slower orbital velocity. With more acceleration and less orbital velocity, the near tide is increased. Likewise, farther parts of the Moon have less acceleration and more orbital velocity, once again increasing the proposed tide. This analysis is once again (mostly) true, but this second cause has nothing to do with gravity. It is an outcome of all circular motion, whether you have a gravitational field or not. Whirl any dimensionally consistent object and the circular motion will create tides in the object just like these, if you apply the forces in the same way.

You will say that a spin dryer or a ride at the fair does not cause elongation like this, forcing the object to spread out along the radial line. Just the opposite: a fair ride or spin dryer causes the object to flatten out along the orbital line. But this is because all the force is applied from the back of the object. If we applied all the gravitational force from the back of the Moon, the Moon would also flatten in this way. No tide could be created at the back, since the force would constrain it, just like the wall of the dryer. The rest of the Moon would feel no force and would be totally unconstrained, except by its inner structure. Feeling no centripetal force, it would naturally follow the vector of the tangential velocity until it too was constrained by the force from behind or by internal structure. This is exactly what happens in the dryer or at the fair.

But if Big Uncle Joe swings you by the arms, you do not flatten out like a towel in the dryer. You flatten out along the radius. The force is applied from the front, and you spread out in a line away from the center, with your legs flying behind you.

A similar example of three forces could be created in the spin ride at the fair, or in a centrifuge. Take three equal weights and tie them to three separate points along the same radial line, at different distances from the center. Get the centrifuge up to speed and measure the forces. The greatest force will be on the one furthest from the center. To see how an object that was a sum of the three weights would react as a whole, subtract the force on the inner weight from the force on each one. The force on the inner one is now zero, the force on the middle one is bigger (middle minus inner) and the force on the outer one is biggest (outer minus inner). The outer weight wants to move away from the center a lot, the middle one less and the inner one even less. This is immediately clear with the outer one. If all three ties were cut simultaneously, then the outer one would move away from the center faster than the middle one. The distance between the two weights would increase. Therefore the outer weight seems to feel a force away from the middle weight. The same is true comparing the inner and middle, although it is a bit less intuitive for some. If the ties were cut the inner weight would move away from the center more slowly than the middle weight. Once again the two weights would increase the distance between them, so that there is a sort of force away from the middle weight once again. If the middle weight is the baseline, then both the outer weight and the inner weight will tend to move away from it. This will make the object deform along the radial line, just like the tides on the Moon.

So, we can add up the effects on the Moon just like on the Earth. We can use the equation
Δa_E = ω²r + GM[1/R² – 1/(R-r)²]
= .000012 + .000024 = 3.6 x 10^-5 m/s²
Δa_S = ω²r + GM[1/R² – 1/(R-r)²]
= 6.9 x 10^-8 + 1.4 x 10^-7 = 2.1 x 10^-7 m/s²

The solar tide on the Moon should be 171 times smaller than the terrestrial effect. More importantly, the visible tide on the Moon should be symmetrical front and back. Is this what we find? Not at all. The Moon rotates relative to the Sun, so we would not expect to find a solar effect on the Moon, beyond a tiny constant shift in the crust opposite the direction of this rotation. The rotation of the Moon on its axis relative to the Sun does not cause a further tide from the Sun, or add to the tidal effect, but it acts to shift the tides we have already calculated, just as the rotation of the Earth shifts the ocean tides, causing them to travel. MM is not aware of any experiments on the Moon to measure lateral shift of the crust in the direction opposite rotation, to verify the relative strength of the solar tide, although this would be a very useful experiment.

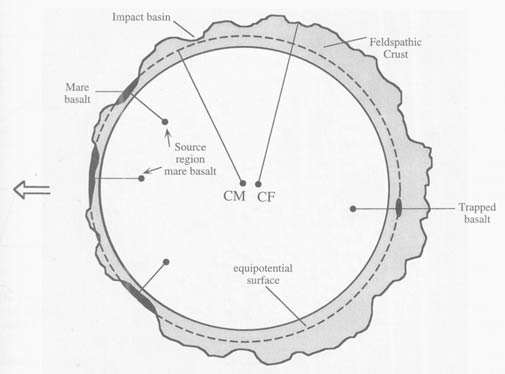
However, concerning the terrestrial tide, we have ample visual data. This data is not a confirmation, to say the least. The schematic of the Moon (above) will show you that the Moon exhibits no real tide at the back. Even more astonishingly, it has a negative tide at the front, the crust being almost obliterated in places. How does current theory explain this? It can't explain it using gravity or circular motion. This is how it is explained in the Encyclopedia of the Solar System (Compiled by NASA and JPL, 1999. p. 252.) The conventional explanation for the center of figure/center of mass offset is that the farside highland low-density crust is thicker. It is massive enough and sufficiently irregular in thickness to account for the effect." More gobbledygook, in other words. If the farside crust is low-density, this would only add to the problem. To create a greater tide we need more mass over there, not less.

Before moving on to solve all these problems, MM has one more thing to say about the orbit of the Moon. In all these analyses, both MM's and those of the Standard Model, it has been assumed that outer parts of the Moon can travel faster than the inner parts. The diagram requires it and so we have just taken it as a given. We do not even ask how it is physically possible for different parts to have different tangential velocities and different orbital velocities. The gravitational field cannot be creating them, since it cannot exert a force tangentially. The field creates only radial forces.

We need either a mechanical cause of the variance, or we need to show that all orbiters exhibit shearing along the direction of orbit. Orbiters in tidal lock should exhibit strong symptoms of shearing, since the forward part of the object is always in lower orbit and the back part is always in higher orbit. The back part of the Moon should shear in the reverse direction of orbit and the front part should shear in the forward direction. But the data is negative, and we are given no cause for the negative data. The only mechanical cause would be some sort of absolute rigidity of the Moon radially. But this is not true empirically. With current theory, the lack of data is a complete mystery.

General Relativity can explain it, since according to that theory, the Moon is feeling no forces. A Moon feeling no forces would not be showing any signs of shearing. But if we use GR to explain the tides we don’t see, then we cannot use Newton to explain the tides we do see. The Moon is either feeling forces or not.

The problem was a big one for Newton, even in his own time, since he is the one who postulated that the tangential part of the velocity in orbit was caused by the orbiter's "innate motion". That is to say, the tangential vector is one the object has prior to or independent of the gravitational field. But of course the object could not have a variable innate motion. It cannot speed up outer parts and slow down inner parts just to suit diagrams.

It is now not just Newton’s problem. Current theory has inherited it and failed to explain it, or even try to explain it.

Analysis of Newton's Proposition 66 from The Principia,
which is the foundation of modern tidal theory

Abstract: MM will analyze Newton's Proposition 66 from The Principia, which is the foundation of modern tidal theory. MM will show that it is false. MM will then show that its extension by Maclaurin is also false. MM will show that current equations fail to predict the known eccentricity of the Moon, being off by a factor of ten. MM will then show the simple math proving that the eccentricity of the Moon is caused by the charge field and the Solar Wind, not by gravity.

Modern tidal theory, like many other things, comes from Newton. Newton was only a beginning, and it is admitted that he made some mistakes, but all the major additions like those of Bernoulli and Laplace and Maclaurin take Newton's basic gravitational theory as given. We can see this in recent modern books like one from 2001 by David Cartwright (of Cambridge and NASA), where the exposition of “correct” tidal theory begins with Newton's Proposition 66, from The Principia. It is this proposition that MM will analyze in this paper.

Basically, this proposition shows a circular orbit thrown into ellipse by a third body. Later tidal theorists (like Maclaurin) then borrowed this proposition to show that the water around the Earth could be taken as a third body, and that it would therefore be thrown into ellipse, creating the tidal bulges we have been talking about in other papers.

Maclaurin won a prize in Paris in 1740 for a paper showing that the Earth would be a prolate spheroid under the influence of the Moon, with major axis directed at the Moon. Maclaurin's attempt to get around the problems by using Newton's three-body equations that create an ellipse, substituting the water around the Earth for the third body does not work. This is where we get the current math and the current illustrations showing bulges. Nothing much has changed in almost 300 years. Unfortunately, Maclaurin's equations were based on models, not on data, and we have since amassed huge amounts of data disproving his hypothesis and math. Bodies don't in fact deform that way, as we can see from our own Moon. The Moon, in tidal lock around a much larger primary, should deform with its major axis pointed at the Earth. But it doesn't. The forward part of the Moon is not heaped, it is obliterated. It has a negative tide. Still today we get Maclaurin's math and illustrations, leading all tidal theory pages.

Newton's proposition was false to as shown below:

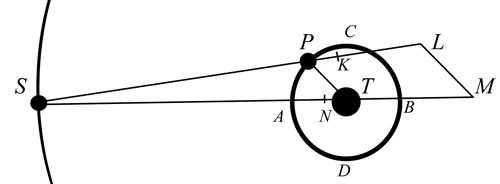
In Proposition 66, Newton gives us two smaller bodies orbiting one larger body. The larger “central” body is T, the nearer orbiter is P, and the distant orbiter is S (see illustration under title). David Cartwright and modern theorists try to get you thinking that S stands for the Sun, but if we look at Newton's initial assignments, we find that is not so. S is orbiting T, so T cannot be the Earth and S the Sun. The Sun does not orbit the Earth, and it was not thought to do so in Newton's time.

The first thing we find if we study Newton's own assignments is that he does not give us any orbital velocities for S and P. He clearly intends that his theorem will be proven for any and all velocities, so that they are not important. However, MM will now show a simple falsification of his proposition, using a set of velocities for S and P. If MM can show one falsification, the proposition, as stated, must be false.

Newton, in his illustration (above), draws S and P initially orbiting T in circles. His claim is that S, the outer moon, will necessarily throw P into ellipse. The case that falsifies that proposition is the case that S and P have the same time of one orbit. In other words, S is traveling much faster than P, so that the two remain in the same position relative to one another. The easiest way to see this falsification is to put P and S in the same line to start with. Nothing in Newton's set-up disallows that. Well, if that is the case, then S and P will remain in a line always, and this will only have the long term effect of increasing the radius of P's orbit. P will be thrown into a bigger circle, not an ellipse.

MM will be told that Newton's math and his proposition also tell us that T will be thrown into a barycenter motion by the attractions of S and P. This must cause an ellipse. No, it causes the appearance of an ellipse only if we measure from T, and if T assumes it is static. But if we measure the orbits from S, P, or any other place in the field other than T, then P remains in a circular orbit. No ellipse is created, and Newton's proposition is false.

MM will then be told that the barycenter causes an ellipse after the fact, since the barycenter creates a wobble. But the barycenter does not create a wobble relative to the two orbiters, if the two orbiters were in round orbits to start with, and if the inner orbiter is not thrown into ellipse. This is because the two orbiters, if they are stable relative to one another, only tend to pull the central body toward them. If they are stable, they pull the central body toward them an equal amount at all times, which means the central body is always the same distance away from them. So the central body can wobble without throwing the orbiters into ellipse.

This also works if S and P are not in a line. They only have to have the same orbital period. This is because P will always have the same force vector from S, and this means that the orbit will be changed the same amount all the way round. If you change a circle the same all the way around, you get a bigger circle, not an ellipse. To create an ellipse, you have to vary the change on the circle. You can do a lot of math to prove this to yourself, but it should be obvious at a glance. The only reason no one saw this with Newton is that he couches everything in stilted and convoluted language, and lots of dense geometry.

Newton's geometry fails because it contains the unstated assumption that S never moves. If S never moves, then Newton's theorem does work: P is thrown into ellipse. But Newton states that S is in orbit around T, and you cannot maintain an orbit with zero velocity. Therefore, proposition 66 is false.

We can see how confused Newton is by looking at cors. 3, 4, and 5. In these, it is clear he thinks that the ellipse is pointy in the quadratures, rather than at conjunction and opposition. In other words, he in not telling us the ellipse is pointing at S, but the reverse. In his corollaries, the bulges are not pointing at the perturber S, the bulges are to the sides. Since his main proposition is false, and his first corollaries are false, we must assume all his corollaries are false.

Newton starts corollary 5 by telling us P is closest to T at conjunction and opposition. He then switches, telling us that IF P were in ellipse to begin with (had an initial eccentricity), then “it may sometimes come to pass” that P would be farther from T at the syzygies. MM takes this to mean that an initial ellipse will be made more elliptical, and that the ellipse will travel.

Newton could have made it easier to understand by drawing an ellipse at some point. But instead he just draws the same circle over and over. He publishes the same stinking diagram six times in this section, and never once draws the ellipse to show us where it is.

Newton then uses the next several corollaries to push the ellipse from the quadratures to the syzygies. He creates several variations or “errors” to make the apsides travel. In the first variation (cor. 6), he lets the force from S vary. This creates a motion of the apsides forward and backward, but “more forwards than backwards.” But, again, he fails utterly to prove this “more forwards than backwards.” He says it is because KL is greater than LM (see diagram), but that is an accident of his diagram. By varying the distance of S, we can make LM equal to or greater than KL. So it is clear Newton is just pushing his numbers here. It is less clear why he is doing it. He wouldn't have needed to push his apsides to the syzygies if he had just found his ellipse pointing at S to start with, as they now do. Modern physicists no longer use this push of Newton, and it is probably because they know it is a push (supposing they can make any sense of this text at all).

But that begs this very big question: if Newton's initial proposition is false and all his corollaries are false, up to corollary 18, why have we built 300 years of tidal theory upon corollary 18? Corollary 18 is where Newton applies proposition 66 to tides. Corollary 18 is one of the shortest corollaries in this section, being less than 15 lines long, but it supports all of modern tidal theory. In it, Newton proposes that we replace the orbiter P by a fluid annulus or ring. “And the several parts of this annulus, performing their motions by the same laws as the body P, will draw nearer to the body T, and move swifter in the conjunction and opposition of themselves and the body S, than in the quadratures.”

That “swifter in conjunction” means that once again Newton has his ellipse pointing the wrong way. The apsides are in the quadratures, which is opposite the modern drawings. More than that, in this corollary 18, Newton never stabilizes his apsides in the syzygies. Yes, he proposes that the apsides move, but they do not move to the syzygies and stop there, as modern theory would have it. No, “the axis will oscillate each revolution.”

Terrible problems there, but we aren't finished. The tides cannot “perform their motions by the same laws as the body P,” because the body P is an orbiter and the tides are not. Apsides are qualities of an orbit, and the tide cannot be assigned apsides. The reason for that is the particles in Newton's fluid ring “move swifter in conjunction;” but the tide cannot move swifter in conjunction. The tide need have no orbital motion, at conjunction or anywhere else, since motion at conjunction is defined as tangential motion uncaused by the field, and the tidal motion, whatever it is, in not motion of that sort.

To say it another way: in earlier parts of The Principia, Newton defines orbital motion as a compound of “innate motion” and centripetal motion caused by gravity. The innate motion is tangential motion that the orbiter carried into the orbit. It is uncaused by the field. But the tides do not and cannot have this motion. Since they are not in orbit, and since they have no innate tangential motion, they cannot “perform their motions by the same laws as the body P.”

Also, if the tidal bulges were created by an ellipse in this way, then that would mean that the bulges were the apsides of the ellipse. Since the Moon travels within 30° of the equator, the tide should travel mainly equatorially, and mainly east to west, with a maximum speed of travel between the two bulges and a minimum speed under the bulges. Is that what we find? Not even close. Even if we give the tide some time lag, it doesn't work at all like that. If it did, we would see the largest tides near the equator. In fact, we don't. The waters of the Earth aren't even trying to orbit the Earth equatorially. If anything, they are moving east to west, because they can't keep up with the rotation of the Earth. That is not an orbit, that is a resistance to an orbit, as we would expect.

Despite all that, Newton tries (cor. 19) to force a comparison to Earthly tides by proposing that his annulus of orbiting water is now matched in speed by the rotation on its axis of T. Note well that Newton simply proposes that the period of rotation of T is the same as the period of rotation of the water. T does not cause the rotation of the water, it simply spins underneath it, the two periods of rotation matching by fiat. Is that really how we think the oceans work? Are the oceans independent of the spin of the Earth, the rotation of the Earth and the rotation of the water just happening to match? We could ask the same question about my couch. Is my couch orbiting the Earth, with a tangential velocity of its own? Or is my couch moving due to direct contact with the Earth? One had always assumed that my couch was just along for the ride, but maybe Newton and modern physicists really believe it is self-propelled.

These analogies are so humorous that it could be mistaken for Jonathan Swift by mistake. Passages like this one have the flavor of the Laputians' floating island, except that Swift's expositions are clearer.

By the way, Newton does get around to switching his bodies, so that by cor. 14, T and P are orbiting S. But if that is the case, we have to ask why Newton didn't just let T and P orbit S to start with. Why do all the math for one three-body problem, then switch the bodies at the last minute? It looks like a shell game to me, and we had better check his proposal. He simply states that all the math will be the same as before, but is that true? It could hardly be true, since in the first case we had two moons orbiting one body, and in the second case we have a planet and a moon circling the Sun. As just one example of how they are not equivalent, let us ask if we can propose any velocities for T and P that will keep S and P in a line. No, if we are given that P is still orbiting T, there is no velocity for T that can change the nature of that orbit relative to S. We cannot maintain constant relationships, and therefore cannot maintain circles.

Modern physicists will say that they do not care about the problems. They only care that once Newton makes the switch, defining S as the Sun, the Moon must be thrown into ellipse. If the Moon is thrown into ellipse, then the tides must be, too. MM does admit that the Moon must be thrown into ellipse, but the problems remain. To start with, physicists now use Newton's math in this section to show why the Moon's apsides travel. The Moon's ellipse does not always point at the Sun. It travels. If that is so, then the apsides of the tide should travel in the same way, by the same general math.

Modern physicists want the apsides of the Moon to travel, since they do, but they do not want the apsides of the tide to travel, since there is no indication that they do. They always draw the tidal apsides pointing at the Moon, and they do that because if the apsides travel, there is no way to get them to meet up with the Solar bulges at the right times. Remember that the spring tide is explained as a conjunction or opposition of the Sun's and Moon's tidal apsides. But if the lunar apsides travel, they can be anywhere. A conjunction of Sun and Moon can explain spring tides only if the tidal apsides follow the position of the Moon. But neither Newton nor Maclaurin or anyone else has shown that they must. In fact, the math shows the opposite. If lunar apsides travel, then tidal apsides should, too. You cannot have it both ways.

Another problem is that by the current equations, the eccentricity of the Moon's orbit should be easy to estimate. The Sun has a force on the Moon 2.2 times that of the Earth on the Moon. At closest approach, the Sun would have an even greater relative force on the Moon. Unless the Moon moved close to the Earth at this time, it would escape. This means that by the current equations, the Moon's eccentricity would be infinity. The Moon would move in a beeline toward the Sun.

Is that what we find? Of course not. The Moon's orbit has an eccentricity of .055, but the current equations predict infinity. Off by a factor of infinity. The current math doesn't work.

Many mainstream scientists must recognize that gravity theory has many problems. But since they see no clear answers, their only hope is that string theory or brane theory may eventually come to the rescue. Until then, they are not prepared to look hard at Newton or Laplace or Einstein or any of the other big names. What we have doesn't work, but it is all we have. Therefore we must defend it, they think. Honorable, in a certain sense, but foolhardy nonetheless. If the various standard models weren't sold and defended with such certainty and gusto, more scientists would be prepared to offer corrections. As it is, only outsiders like me are “allowed” to spend any time studying alternatives. Peer pressure prevents academics from doing basic science. Only a handful of top theorists are allowed to speculate, and they have proved that they are not able to solve this one. After a century of work, they have only muddied up the water even more with all their new maths and their fancy lingo. Rather than correcting Newton or Laplace or Einstein, they have only whitewashed the old theories with ever more coats of obscuring equations. But as we have seen here, Newton was already dense and opaque enough. We did not require more density, complexity, and opacity, we required a clean-up. Now, 300 years later, we require a much larger clean-up.

Gravity by itself cannot explain tides, it cannot explain perturbations (Laplace Three Body Problem on MM site), it cannot explain resonances, and it cannot explain the size of ellipses (the actual eccentricities we see). To really begin to explain all these things, we have to have two fields, gravity and E/M. We have to have a unified field, and we have to have a unified field where E/M is large enough at the macro-level to enter the equations.

In Solution to the Ellipse problem it has been shown that ellipses aren't caused by gravity at all. Ellipses are an E/M phenomenon, caused by charge field interaction. MM will now show the cause of the Moon's eccentricity very quickly and directly. That number .055 is the same as 1/18, so all MM has to do is show why the Sun's field is 1/18th that of the Earth. In Spring and neap tides are caused by the Solar Wind, it can be seen that the Solar Wind supplies a force 2/5th that of the Moon's force on the Earth. That was MM's explanation of the spring and neap variations. So we just need to find the Solar Wind force as a fraction of the Earth's force on the Moon. Let's do the math in reverse, to see what number we would need to find. Obviously, we need to find that the Earth's force on the Moon is 7 times the Moon's force on the Earth. Because 2/5 x 1/7 ≈ 1/18. Fortunately, MM has already shown that math elsewhere. In Newton's law is a Unified Field of Gravity and E/M, MM said it this way:
So, if the Moon’s (radius x density) is 1/6 that of the Earth, then if the Moon’s number is 1, the Earth’s number is 6. And the total number for the combined field would be 7. But we want to give the entire effect to the Moon, keeping the Earth as a fixed point. So we multiply .151 x 7 to get 1.057m/s².

That is how fields work. And that is where the number 7 comes from. The Earth's charge effect on the Moon is 7 times the Moon's charge effect on the Earth. Therefore, the Solar Wind's effect on the Moon is 1/18 that of the Earth's charge effect on the Moon. And that gives us the Moon's eccentricity of .055. The Moon's ellipse is caused by charge, not by gravity. Newton's first postulate was wrong. He began by assuming that bodies influenced each other by gravity. But, in this case, they don't. Ellipses aren't caused by gravity. Neither are perturbations or axial tilts or resonances. This is not to say that MM decided to ditch gravity. He has not. MM keeps it in these unified field equations, and it is just as strong as it ever was. In fact, it is stronger, shown at G is the Key to the Secret of Gravity increases its power there by a factor of 10²². But in this problem, as in all others, we have to monitor both gravity and the charge field. It turns out that ellipses are caused by the charge field.

Exploring the E/M Solution of Tides

To support the E/M field solution, a few facts are of very relevant: 1. The Moon shows a negative tide in front, where it should show a positive tide. 2. The crust of the Moon has been partially obliterated by some influence from the Earth, but the standard model has no mechanism to explain this negative tide. Considering that the E/M field is a bombarding field explains this all at once.

If the Moon is being bombarded with photons from the Earth, as the primary mechanism of tides, we would expect the front of the Moon to be obliterated by them. Since the photons are real and the bombardment is real, the Moon must be damaged just as if the Earth were constantly firing bullets at it. First, the math for the Moon's influence on the Earth will be shown, but later how the Earth affects the Moon.

The most astonishing thing about MM's Unified Field is that small objects have stronger E/M fields than larger ones. Given two spherical objects of equal density and make-up, the smaller of the two will have a stronger E/M field, not just relatively, but absolutely. The Moon has a field that is 110 times stronger than the Earth's field. This fact seems counterintuitive at first, but a little consideration shows that is completely logical, given the things we already accept about our universe and the way it works. All we have to do is postulate that the E/M field is a real bombarding field or radiation field made up of much smaller bodies.

This field is being emitted by every single atom in the field (and even by the electrons in the atoms). Therefore, any field of atoms of any size will create the same E/M field density, provided that the density of the atoms remains constant. A small area of atoms will create the same field as a large area of atoms. If we look at areas that are cubic, then at the edge of any size cube we will find the same E/M field density, given an equal density of atoms in the cube. It does not matter if our cube is one meter across or one light year across.

But if we look at areas that are spheres, we find something strange. If we postulate that all the radiation is emitted radially, as if from the direction of the center, then smaller spheres will create much denser E/M fields than larger ones. This is due to the ratio of the surface area to the volume, of course. A smaller sphere will have the same ratio of mass to volume as a larger sphere, by the definition of density. But it will have a larger ratio of density to surface area, which proves MM's point.

This is a bit confusing, so think of it this way: the smaller sphere focuses the charge that is emitted, creating a greater charge density. A larger sphere will emit more total charge, of course, but if we look at the amount of charge emitted from a given radial line, the smaller sphere will actually emit more. This is because there are fewer such radial lines with the smaller sphere, so more density has to go with each line. Or, just reverse this logic: as we move to larger spheres, the same density has to emit through a greater surface area. Since the surface area increases faster than the radius, the charge will dissipate into space more with a larger sphere than with a smaller sphere. This is important when we are looking at tidal influences between celestial spheres like the Earth and Moon, and we will see the importance later with other charge influences (described at MM site), like those that cause axial tilt and Bode's law. When looking at linear influences between planets, the charge density is more important than the total charge.

In another paper, MM has shown that, given a density of atoms in a sphere, the E/M field density outside that sphere drops off by 1/R⁴, MM was able to prove this by looking only at the known gravitational numbers from the Moon and Earth, and subtracting out the acceleration fields. The radius of the Moon is 1/3.67 that of the Earth and its density is 1/.6057, which gives a field strength of 110 times that of the Earth. If the Moon had the same density as the Earth, its E/M field would be 182 times that of the Earth, as a matter of charge density.

According to this theory, the Sun would appear to have no possible effect on the Earth's tides. Its surface area overwhelms its density in this regard, and then we add the distance, which must also dissipate the field. Unless the Sun's density is very much greater than we think it is (1408), its effect must be negligible. Let's do the math. The Sun's density is about 1/4 that of the Earth. If the Sun were the same size as the Earth, its E/M field would also be 1/4. But its radius is 109x that of the Earth. So it’s E/M field at the surface would be,

(.009545)332,900/(11,990)3.92 = .0676 m/s²
At a distance of 1AU, this field would be
(.0676)(696,000/1.5 x 10⁸)⁴ = 3.13 x 10^-11m/s²

Because the Sun is a giant fusion reactor, we do get electromagnetic effects of other sorts here on Earth. Solar flares, solar wind, etc. These cause very positive E/M responses on Earth, as everyone knows. But the standard E/M field of the Sun is caused only by the density and type of atoms present, and that field appears too weak at the distance of 1AU to cause tides. Unless it is postulated that fusion creates a constant boost in the E/M field, it would appear at first glance to be impossible to link the Sun to terrestrial tides. (The standard model has not made this postulate or they would included it to answer the gaps in tidal theory).

In Perihelion Precession of Mercury Explained MM has shown that the Sun causes a large precession due to curvature on the Earth (3.36 arc sec), which would imply some great force, but this precession due to curvature or expansion is not a force at all. That is to say, it is not caused by a real radiation field. It is caused by apparent motion due to expansion. This is clear from MM's simple diagrams, where MM shows that this bending—whether applied to starlight or to precession—can be attributed to expansion alone. Whether you think it is caused by curvature or expansion, it is an effect of the competing acceleration vectors. It has nothing to do with electromagnetism or any other emitted field.

Others will laugh and say, "By your theory of increase (1/R⁴), a satellite 1km across with a density the same as the Moon will have an acceleration at its surface of 10¹³m/s², all due to electromagnetism. It would act like an inverse black hole. And a proton with a density of the Moon would have an acceleration of 10⁸⁵m/s²."

Stated in that way, it seems like a dead end, but maybe it is because the electrical field and gravitational field have to be taken in tandem now. This E/M acceleration we are finding has to be applied to the mass that is producing it, and mass is now a function of acceleration, too. As you have seen, mass and gravity are two names for the same fundamental acceleration, which MM has shown is L³/T² in Newton's law is a Unified Field of Gravity and E/M. Therefore, we cannot just compare accelerations directly; we have to look at velocities, too.

To take a specific example, MM has shown that the Moon has an acceleration due to mass/gravity of 2.67m/s². So assuming v_o = 0, after 1s it will have a velocity of 1.335m/s. That is the velocity and distance in which we now must place the E/M acceleration. But if we look at a marble with a radius of 1cm and the same density as the Moon, it will have an acceleration due to mass/gravity of 1.54 x 10^-8 m/s² and a velocity of 7.68 x 10^-9 m/s. If we apply the E/M acceleration to this velocity, we obviously get a much smaller effect.

You see, with the new theory of a compound field, and mass and gravity as acceleration, all things are not in equilibrium regarding velocity. Before, it was thought that things were in equilibrium regarding a velocity due to expansion, since they were not expanding. But now the equilibrium is given only to the relative size. Things still remain the same size relative to each other, since we must keep a visually consistent universe. But velocities are not equal, as MM just showed. Since dv’s are not equal, accelerations cannot be compared directly. The only time that accelerations can be compared directly is when they are taken from objects close in size. The radius difference between the Moon and Earth is only a factor of 3, so the accelerations of Earth and Moon can be compared pretty much directly. But when we compare the computed acceleration of the Moon to a little marble, we can’t do a direct comparison. The Moon is moving so much faster during each dt.

It will be said that this offsets only part of the huge numbers, and that is true. There are other factors. Let us start with the proton problem and see what has to be done. There is an acceleration of 10⁸⁵ to account for. Well, the standard model says that the electrical field is 10⁴⁰ more powerful at the quantum level than gravity, so MM only has 10⁴⁵ to account for now. MM has shown that the number is a relative number (E/M field relative to gravity field) not an absolute number, so MM is halfway there.

In calculating the difference in field strengths at the quantum level, the standard model assumes the gravitational field decreases with the square of the distance. This has been shown to be false. The inverse square law applies to the E/M field part of the Unified Field Equation, which means that gravity is some 10²² stronger at the quantum level than they thought. That brings me to within 10²³. MM has just shown that the velocity due to mass of a 1 cm marble is 10^-9, so a proton would have a velocity due to mass of 10^-22. That leaves me 10¹ out of 10⁸⁵.

Not a bad margin of error for such a quick analysis. And MM did not even have to discuss the density of the proton, which would of course give me more room to play, since it is unknown. Numbers can be obtained from quantum section of G is the Key to the Secret of Gravity.

The easiest way to see that the numbers must resolve in much the same way they always did is to recognize that one simply needs to give the 1/R² that we used for gravity to the E/M field instead. This makes E/M 1/R⁴ while gravity becomes directly proportional to radius.
Before: gravity is 1/R² and E/M is 1/R²
After: gravity is 1/R and E/M is 1/R⁴

If the Sun is not a cause of tides, then we must rule out Venus and Mars as well. This leaves us with only the Moon. How can the Moon cause all the variations we see?

Since the mechanism was always assumed to be the gravitational field, all the historical (and current) explanations have been spectacularly flawed and simplistic. The basic mechanical explanation, one that is still trumpeted by major websites and institutions, is the heaping of waters nearest and farthest from the Moon (with some delay). This mechanism is so naïve it is pathetic to ponder. Even were the force caused by the Moon's gravity, it seems the shape of the field might have been taken into account by these magnificent theoreticians. A force, of whatever kind, emitted spherically by the Moon, must arrive at the Earth spherically. Assuming the field is traveling at or near the speed of light, we can imagine no delay more than a second or two. So the position of high tides relative to the Moon cannot be pushed very far. They must be looked for in very specific places at very specific times, and since this has never been done, we can call it gloriously negligent.

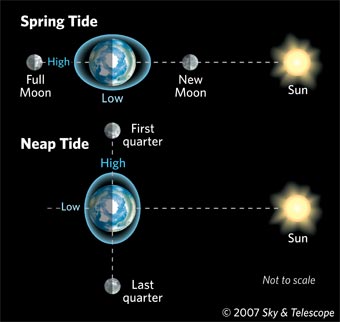
To show the degree of this negligence, let us return to the internet. Wiki presents us with a new illustration to show the spring tide, which puts the Moon and Sun on opposite sides of the Earth. The same thing happens with the Moon and Sun on the same side, but this illustration is better propaganda, since it appears to show the tides being created by direct pulling action. The problem is, to get the correct tidal mechanism working with the Sun on both sides, you have to treat the field as a differential field. This differential field creates tides both front and back, and it does so with either Sun or Moon. But if gravity really creates such a differential field, it must do so with the barycenter motion as well. Amazingly, the standard model still trumpets the barycenter, even in tidal theory, as you will see from looking at the new Wiki page. This is a problem, since the differential field of the barycenter would create tides that totally swamped the Sun and Moon tides, making this spring and neap tide illustration moot. No matter how you look at it, with either gravity as a direct pulling force or with gravity as a differential field, spring and neap tides cannot be explained. This is why Wiki pulled the full mathematical analysis: the differential explanation does not work. This illustration is a fraud.

It is amazing to find that tidal theory still rests on Newton, Maclaurin, Euler and Laplace. It should be highly embarrassing to have nothing to add to this after hundreds of years. Is no one capable of doing a little independent thought? Must we continue to stupidly parrot Newton and Laplace until the end of time?

Here is possibly the meatiest paragraph on the whole new Wiki tidal page. It is the closest the new author gets to doing any math:

The depth of the oceans is much smaller than their horizontal extent; thus, the response to tidal forcing can be modelled using the Laplace tidal equations which incorporate the following features: (1) the vertical (or radial) velocity is negligible, and there is no vertical shear—this is a sheet flow. (2) The forcing is only horizontal (tangential). (3) the Coriolis effect appears as a fictitious lateral forcing proportional to velocity. (4) the rate of change of the surface height is proportional to the negative divergence of velocity multiplied by the depth. The last means that as the horizontal velocity stretches or compresses the ocean as a sheet, the volume thins or thickens, respectively. The boundary conditions dictate no flow across the coastline, and free slip at the bottom. The Coriolis effect steers waves to the right in the northern hemisphere and to the left in the southern allowing coastally trapped waves. Finally, a dissipation term can be added which is an analog to viscosity.

Wiki's hired pro still can't spell or use the English language, but so what? More important is that this entire paragraph, though trying to be rigorous, is nothing but niaiserie. It is bushwa, babblement. Laplace's tidal equations are all based on gravity as the mechanism, so they are worthless. But even if Laplace had based them on the E/M field, his postulates would still be illogical. Laplace loved mathematics, but he was very thin on mechanics. His first postulate cannot be true. As MM will show, the vertical or radial force must be significant and non-negligible, and so must the velocity created by it. Which also falsifies the second postulate. Concerning the third, the Coriolis effect is a tertiary or lower effect, which does not need to be addressed until the major mechanisms are sorted through. It is a terrestrial stirring of the tide, not a creator of the tide. It is here only to give the author more words to capitalize and more esoteric names and effects to drop. And the fourth postulate is just absurd. Here we have been inundated with false mechanics in order to avoid the real questions. Laplace's equations won't tell us where the high and low tides are, and why, but they claim to tell us that variable tangential velocity at different depths is enough, by itself, to cause the rising and the falling. As if tangential velocity, by being variable, becomes anti-gravitational. The author must bury this in the most impenetrable language ("negative divergence of velocity"), otherwise the casual reader might recognize it for the flapdoodle it really is. Then, to finish up, we are treated to trivial "boundary conditions". As if we need to hear about boundary conditions when a basic mechanism has not even been offered.

Before we look for the position of high tides, let us calculate the force from the Moon. How does the E/M force compare to the gravitational force that was thought to apply? It is stronger or weaker? Let us take some numbers from MM's previous papers. It was found that the acceleration due to the E/M field of the Moon is 1.051 m/s^2**, but this is at the surface of the Moon. This acceleration will dissipate with distance, since the field spreads spherically. In fact, it diminishes at R⁴, so we find, at the surface of the Earth,

a/1.050 = (1,738/378,022)⁴
a = 4.7 x 10^-10m/s²

MM said above that the charge from the Sun seemed to be negligible, but now that we see the force from the Moon, we find it is only 15 times the force from the Sun. Therefore we may be able to bring in the charge from the Sun as one of the lesser harmonics later (possibly what is now called the Solar diurnal). But it is still not large enough to explain the 46% Solar input we are trying to explain.

The acceleration from the Moon looks too small to do anything, but we have a vector situation here. The Moon is repulsing the Earth and the Earth is repulsing the Moon, so the total repulsion will be a summation of the two. MM has shown that the total acceleration of the combined field is .151m/s², but that isn't the number we need here either. What we need is the Earth’s E/M field acceleration at its surface, .009545m/s².⁽²⁾

By this way of looking at it, the Moon’s field is almost negligible. All it does is give the Earth's field something to bite on. Ironically it appears that all the effects of foreign bodies turn out to be negligible. First the Sun and now the Moon. The Moon only supplies a force to be resisted—an acceleration that awakens the Earth's own E/M field acceleration.

But why is the "bite" at the level of the Earth's oceans, and not at some level in space halfway between the Earth and Moon? It is simply because the acceleration has to have something to accelerate. The combined E/M field has to have a place to work itself out, and the Earth's oceans are the nearest material field. The fields can’t meet in space, since E/M fields don’t work like that. A field cannot express itself upon another field, since the particles in the field are too tiny. A field must express itself in a material field, an atomic or molecular field. We already know that from QED, but it is good to be reminded of it in this place. Of course, in the ionosphere, we do have an ionic field, and we do see lesser effects from this same cause there. But this isn't the time to get into all that.

Now that we have a new number, we can compare it to the old number. What was the size of the acceleration due to gravity, which was thought to cause tides? Well, the acceleration due to gravity at the surface of the Moon was thought to be 1.62m/s², until it was shown that acceleration was a compound number. The acceleration was thought to diminish as R², so the acceleration at the surface of the Earth due to the Moon would have been a maximum of

3.34 x 10^-5 m/s² or .0000334 m/s².

Having previously shown the problems with tidal theory, MM found that the standard model now finds an acceleration from the Moon of Δa = 1.14 x 10^-6 m/s², using the differential field. They try to add 50% more to that, but MM shows they cannot logically do so, since the Earth is not orbiting the Moon. Either way, with the differential field or the straight gravitational field, the acceleration is much smaller than is attainable from the E/M field.

Somewhat shocking to have found 286 times as much force using the E/M field as Newton found using gravity. And we found it all coming from the Earth itself.

What more shocking is yet to come. All the numbers above come from the E/M fields that have been segregated out of the compound fields of Newton and Einstein. But this force of the Earth's E/M and the Moon’s E/M coming together must still meet the Earth's acceleration due to gravity. For at the same time that the two E/M fields are meeting in the upper levels of the ocean, the Earth is accelerating at 9.81m/s². One can give this acceleration to the field or to the Earth, but MM has shown that as a vector, this acceleration must be in opposition to the E/M field. [It is 9.81, not 9.8, since MM has proved that the solo gravitational field (without the E/M field) is a fraction more than we thought. We have been measuring a compound field all these centuries. But now we subtract out the E/M field, and we have 9.81.] This means that at the center of our circle, we must add 9.81 to .009545.

Good lord, you say. That would mean that a person would weigh more than double directly under the Moon! So let me put it another way. These vectors are difficult to keep in line. When one says that we must add 9.81 to .009545, that is the same as saying that we must add .009545 to 9.81. Whereas, normally, we would subtract .009545 from 9.81, to get our old friend 9.8. That is how the two fields work when no other body is causing tides. The gravitational force pulls us down, as an effect, and the E/M field pushes us up, as an effect, so the result is mostly down, to the tune of 9.8.

But now MM is now saying that instead of subtracting, we add. The Moon causes the vector situation to switch. So now, directly under the Moon, we have about 9.82 m/s² as our resultant acceleration. And this makes the tidal acceleration

.009545 x 2 = .0191 m/s²
And that is 572 times the maximum tidal force from gravity.

So, yes, you would weigh about .2% more directly under the Moon. (no prediction; just doing the math.) But don’t be too surprised, since this was an effect of the old tidal theory, too. Except that you would have weighed .00035% less. MM is changing the size and direction of the change, but the idea is not all that different.

There is still a question not resolved and that is the reason why the Moon's presence appears to switch the direction of the Earth’s E/M field vector so that he two E/M fields are added together? But this result was added to the Earth’s acceleration. How can that sense because the entire Unified Field Theory seems to show that the E/M field vector is in opposition to the gravitational acceleration? Yet if the vector is in opposition, it must point out. That is why it repulses the Moon. The E/M field is a repulsive field, according to all your novel theories. If so, the Moon cannot reverse the direction of the Earth's E/M vector just by sending in a negligible amount of force (.00000000047m/s²).

Again, the problem is one of vectors. Yet as effects, the vectors of gravity and E/M are in opposition: the gravitational acceleration creates an apparent motion of attraction (the bodies get nearer) and the E/M field creates a real repulsion (the bodies get farther away). But as real motions, the gravitational acceleration and the E/M field are in the same direction. The surface of the Earth is moving outwards. The Earth is also emitting radiation, and this radiation is moving outward, bombarding all things. So in this case the vectors are not in opposition.

This means that when you are solving a problem, you have to be aware of which vectors you are talking about. Are you talking about force vectors, as seen by real eyes or instruments; or are you talking about acceleration vectors that describe the actual motion of the quanta? They aren't the same.

The Moon's presence seems to reverse the E/M field vector of the Earth, because when the Moon is present, we stop looking at the E/M field as an emission of the Earth and start looking at it as a product of the Earth/Moon interaction. We stop looking at it as an acceleration and start looking at it as a force. As an acceleration, we subtract it from the gravitational acceleration, since their effects are in opposition. As a tidal force, we add it to the gravitational acceleration, since they are a vector summation.

This can be stated more briefly in this way: when two vectors are drawn in opposition, they can either be added or subtracted. If the vectors are meant to represent a collision of particles, they are added, since forces in collision add. If the vectors are meant to represent velocities or accelerations that do not collide, then they are subtracted.

Looking ahead, we see many things:

we have to include the idea that we have a continuous source of waves from both the center and the outer rim.
we have to let the waves travel to the far side of the Earth, where they will interfere
the interference waves have to travel back to the near side, where they will interfere with the source.
the Earth’s rotation has to be taken into account, making the continuous sources travel in a westward direction (as a first approximation).
spring and neap tides in a logical way, without the Sun's gravitational field (See Spring and neap tides are caused by the Solar Wind)

But before this, we have to look at one other major factor: the magnetic component of the field. Since with the central force we are looking at lateral results, we must remember that the magnetic field also works in this direction. So far all the forces MM has postulated and calculated have been electrical forces. But the E/M field has two components. By the right hand rule, if the electrical force is radial down, then the magnetic force will be clockwise, looking down on the ocean. Toward the center of our circle, this should have a magnifying effect on the electrical force, giving it the effect of a screw instead of a nail. This is true whether you imagine once big screw or billions of tiny screws. If the screws were impacting a solid, this would not be true regarding the tiny screws, but since we are dealing with a liquid, we have freedom of motion in all lateral directions, near the surface. The screws therefore cause a spreading, which magnifies the lateral forces already in play with the electrical field. The magnetic field and the electrical field work in tandem to produce the central wave.

At the periphery of our initial circle of influence, we find a different mechanics at work, regarding both fields and their confluence. At the tangent, we have the Earth's force meeting the Moon's, to create a resultant acceleration. But the collision is not head-on. The two electrical forces, by themselves, are orthogonal. This must cause a great reduction in the resultant force, and also cause an angle in the motion of the resultant vector. It will affect the magnetic field as well, since it must suffer the same diminishment. In both cases we will be taking sines or cosines of accelerations instead of the accelerations themselves.

Solution to Tides

At first MM believed that Newton's and Einstein's equations could be made to work because he knew that both field equations already contained the E/M field. That is to say, both Newton's and Einstein's equations describe a compound or resultant field. However, tides are caused completely by the E/M part of this field and not at all by the gravitational part.

Although MM has shown that gravity is just an acceleration, and that there is no real force imparted by the field, many phenomena have apparent motions caused by the gravitational field that are very real. That is, they are not caused by a push or a pull, but they are measurable phenomena. They register on our eyes and instruments and therefore are just as physical as anything else. Einstein showed that geometry is just as physical as mechanics, and he was certainly correct. One such phenomenon is precession. Another is the orbit itself, both its shape and its very existence. But tides are not geometric phenomena. They are not caused, in the first instance, by curvature, expansion, Relativity, the time differential or separation, or by any point-of-view considerations and they have nothing at all to do with gravity.

To solve the problem of tides, it is necessary to separate out the E/M field completely from the combined fields of Newton and Einstein. In "Newton's law is a Unified Field of Gravity and E/M", MM demonstrates how Newton's gravity equation can be separated into two components: gravity and E/M field. With the E/M extracted it is possible to compare the E/M field strengths of the Sun and Moon as measured here on Earth, and finally solve the problem of tides.

Before doing the math on the E/M field, proving that it fits the data, one must remember that the Moon shows a negative tide in front, where it should show a positive tide. The crust of the Moon has been partially obliterated by some influence from the Earth, but the standard model has no mechanism to explain this negative tide. My use of the E/M field as a bombarding field explains this all at once. If the Moon is being bombarded with photons from the Earth, as the primary mechanism of tides, we would expect the front of the Moon to be obliterated by them. Since the photons are real and the bombardment is real, the Moon must be damaged just as if the Earth were constantly firing bullets at it. In this first part, MM will be showing the math for the Moon's influence on the Earth, but in later parts MM will be able to show mechanically how the Earth affects the Moon.

The most astonishing thing MM has discovered in his Unified Field is that small objects have stronger E/M fields than larger ones. Given two spherical objects of equal density and make-up, the smaller of the two will have a stronger E/M field, not just relatively, but absolutely. The Moon has a field that is 110 times stronger than the Earth's field. This fact seems counterintuitive at first, but a little consideration shows that is completely logical, given the things we already accept about our universe and the way it works. All we have to do is postulate that the E/M field is a real bombarding field or radiation field made up of much smaller bodies. (The standard model now does make this assumption, finally admitting that the field must be physical and must be mediated by photons.) This field is being emitted by every single atom in the field (and even by the electrons in the atoms). Therefore, any field of atoms of any size will create the same E/M field density, provided that the density of the atoms remains constant. A small area of atoms will create the same field as a large area of atoms. If we look at areas that are cubic, then at the edge of any size cube we will find the same E/M field density, given an equal density of atoms in the cube. It does not matter if our cube is one meter across or one light year across.

But let us move on. If the Sun is not a cause of tides, then we must rule out Venus and Mars as well. This leaves us with only the Moon. How can the Moon cause all the variations we see?

Before we look for the position of high tides, let us calculate the force from the Moon. How does the E/M force compare to the gravitational force that was thought to apply? It is stronger or weaker? Let us take some numbers from MM's previous papers. MM found that the acceleration due to the E/M field of the Moon is 1.051 m/s See Newton's law is a Unified Field of Gravity and E/M for this number), but this is at the surface of the Moon. This acceleration will dissipate with distance, since the field spreads spherically. In fact, it diminishes at R4, so we find, at the surface of the Earth,

a/1.050 = (1,738/378,022)4 a = 4.7 x 10-10m/s2

The acceleration from the Moon looks too small to do anything, but we have a vector situation here. The Moon is repulsing the Earth and the Earth is repulsing the Moon, so the total repulsion will be a summation of the two. MM has shown that the total acceleration of the combined field is .151m/s2, but that isn't the number we need here either. What we need is the Earth’s E/M field acceleration at its surface, .009545m/s2.(*2)

By this way of looking at it, the Moon’s field is almost negligible. All it does is give the Earth's field something to bite on. It is ironic that all the effects of foreign bodies turn out to be negligible. First the Sun and now the Moon. The Moon only supplies a force to be resisted—an acceleration that awakens the Earth's own E/M field acceleration.

Now that we have a new number, we can compare it to the old number. What was the size of the acceleration due to gravity, which was thought to cause tides? Well, the acceleration due to gravity at the surface of the Moon was thought to be 1.62m/s2, until MM showed that acceleration was a compound number. The acceleration was thought to diminish as R2, so the acceleration at the surface of the Earth due to the Moon would have been a maximum of
3.34 x 10-5 m/s2 or .0000334 m/s2.

Previously, MM showed that the standard model now finds an acceleration from the Moon of Δa = 1.14 x 10-6 m/s2, using the differential field. They try to add 50% more to that, but MM shows they cannot logically do so, since the Earth is not orbiting the Moon. Either way, with the differential field or the straight gravitational field, the acceleration is much smaller than MM has shown is attainable from the E/M field. This is the shocking discovery that there is 286 times as much force using the E/M field as Newton found using gravity and it is all coming from the Earth itself.

These numbers above come from the E/M fields that MM has segregated out of the compound fields of Newton and Einstein, but this force of the Earth's E/M and the Moon’s E/M coming together must still meet the Earth's acceleration due to gravity. For at the same time that the two E/M fields are meeting in the upper levels of the ocean, the Earth is accelerating at 9.81m/s2. You can give this acceleration to the field or to the Earth, but MM has shown that as a vector, this acceleration must be in opposition to the E/M field. [It is 9.81, not 9.8, since MM has proved that the solo gravitational field (without the E/M field) is a fraction more than we thought. We have been measuring a compound field all these centuries. But now MM subtracts out the E/M field, and we have 9.81.] This means that at the center of our circle, we must add 9.81 to .009545.

This is strange as it would would mean that a person would weigh more than double directly under the Moon! So let me put it another way. These vectors are difficult to keep in line.When MM says that we must add 9.81 to .009545, that is the same as saying that we must add .009545 to 9.81. Whereas, normally, we would subtract .009545 from 9.81, to get our old friend 9.8. That is how the two fields work when no other body is causing tides. The gravitational force pulls us down, as an effect, and the E/M field pushes us up, as an effect, so the result is mostly down, to the tune of 9.8. But now MM is saying that instead of subtracting, we add. The Moon causes the vector situation to switch. So now, directly under the Moon, we have about 9.82 m/s2 as our resultant acceleration. And this makes the tidal acceleration
.009545 x 2 = .0191 m/s2
And that is 572 times the maximum tidal force from gravity.

So, yes, you would weigh about .2% more directly under the Moon. But don’t be too surprised, since this was an effect of the old tidal theory, too. Except that you would have weighed .00035% less. MM is changing the size and direction of the change, but the idea is not all that different.

There is still one final question: Why does the Moon's presence appear to switch the direction of the Earth’s E/M field vector? MM said that when the two E/M fields met, we added them together, which made some sense. But then MM said that we added this result to the Earth’s acceleration. How does this make sense, when MM created an entire Unified Field Theory to show that the E/M field vector was in opposition to the gravitational acceleration? You will say, "If the vector is in opposition, it must point out. That is why it repulses the Moon. The E/M field is a repulsive field, according to all your novel theories. If so, the Moon cannot reverse the direction of the Earth's E/M vector just by sending in a negligible amount of force (.00000000047m/s2)."

Again, the problem is one of vectors. MM has shown that as effects, the vectors of gravity and E/M are in opposition. The gravitational acceleration creates an apparent motion of attraction (the bodies get nearer) and the E/M field creates a real repulsion (the bodies get farther away). But as real motions, the gravitational acceleration and the E/M field are in the same direction. The surface of the Earth is moving outwards. The Earth is also emitting radiation, and this radiation is moving outward, bombarding all things. So in this case the vectors are not in opposition.

Now, where do we look for high tides, in the first instance? Let us say that we have just turned on the E/M field, and we want to see where the very first effects are. We let the field travel from the Moon, spherically, and look where it draws a circle on the Earth. There we should find a complete circle of high tides, surrounding a very large low depression. On the far side of the Earth, we would expect no primary effects, only secondary effects, and we will look at those in Part 2. All we can be certain of is that there will be no heaping or depressing over there at first, since nothing is over there to mechanically cause such a thing.

The two spheres of Earth and Moon-field meet at an angle, as in the diagram.

r = 6,378km
R = 384,400km
S = 378,022km
r2 = x2 + (r/2)2
x = 5524km
sinθ = 5524/6378
θ = 60°
2θ = 120°

So the high tides will make a circle with a radius of 6,679km on the curved surface of the Earth. The diameter of influence of the field is initially 13,358km, which is exactly 1/3 of the circumference of the Earth.

Is the number 3 a coincidence? No, it is not. You may assume that any number that precise and that small is not a coincidence, but in this case it is quite easy to show its cause. The cause is the density and radius of the Moon, compared to the Earth. The Earth’s density is 1.65x the Moon’s, and its radius is 3.67x. 3.67 x 1.65 = 6

Not only the strength of the E/M field but its rate of dissipation are determined by density and radius. In the diagram, we are letting the field dissipate with time, in a spherical fashion, as you see. And we are holding the Earth steady. This last is why we find 3 instead of 6. Because we are holding the Earth steady, we are calculating only half of the field changes. We are calculating the Moon’s field moving toward the Earth, but not also the Earth’s field moving toward the Moon. It is an equal and opposite reaction, so it will double the compound field. But we are only calculating the action, not the reaction, so we get half, or 3.

If that was not clear, think of it this way: the orbital distance of the Moon is not a coincidence. MM will show this in more detail in another paper; it is not the subject of this one. But the orbital distance, which we are calling R here, is a direct outcome of the two fields, E/M and acceleration (gravity). These two fields cause the orbital distance. The acceleration creates an apparent attraction, and the E/M field keeps the Moon from being caught. The Moon's "innate" velocity is also involved, of course, but the two fields determine this as well, after any amount of time.3 So R is completely determined by the size of the bodies and their densities. The Moon must orbit at (or near) that radius where its field intercepts 1/3 of the Earth's sphere. Study the diagram closely. It is a lovely thing in many ways. It almost looks like a piece of astrology, except that all the coincidences are now explained with simple and clear mathematics and mechanics.

[Some have looked at MM's diagram and said that the number 1/3 is not even dependent on the Moon; it is dependent on the two small circles MM has drawn. But this is not true. If this is not clear at first, consider the variable t that MM has marked. That is the differential that brings the Moon into the equation, and it does so since that differential is not arbitrary or accidental. You see, the question is, how far do you let the two spheres of Earth and Moon interpenetrate in the diagram? Which is the same as saying, what is the initial interval of influence? It can’t be instantaneous, so what number do we use? We can’t just draw the larger of the two big circles and do the math with it, since it does not correspond to the first touch at the center. We have to let the first influence wrap around the Earth, you see, and this is impossible to draw. The best way to diagram the interval is therefore the way MM has done. This of course begs the question, "What is the value for t?” This brings us to some more math that isn't crucial to the main argument of this paper (It is in an endnote ^*4)

So we have found the size of the acceleration and its initial shape, when it first meets the Earth. What then? From the illustration we can see that the first force will be nearest the Moon, but the other forces in the great circle must come split seconds later. Therefore the initial time lag is not terribly important. What is more important is the direction. In the center of the circle the force is radial. In other words, it comes straight down upon the ocean. We cannot say that this force is unimportant, and that is why MM said that Laplace's first postulate was wrong. First of all we have a force that is 572 times any force Laplace could have been working with, most of it generated by the Earth itself. Secondly, this is a force down instead of a force up. A force of that magnitude over that area cannot be negligible.

You can see that the initial force will change from radial to tangential as we go out from the center of our circle. All around the circumference of our circle of initial influence, the force will be completely tangential. But unlike Laplace, M fines the tangential force less important than the radial. You will soon see why.

Let's look at depth of penetration. At the actual tangent, the depth of penetration will be almost nothing. The force will be like that of the wind. It will be expected to cause waves, not tides. Only as we move inward from the outermost points of our circle of influence will the depth of penetration become significant, and this depth will be caused by an increasing radial component of the force. This contradicts Laplace once again.

But let's be generous for a moment and try to find an instance where Laplace was correct. If we move inward on the circle a few kilometers, we can cause our force to penetrate to some depth without losing much of its tangential component. We have a nearly tangential force that causes a nearly tangential velocity of the waters. This is the component that Laplace took such interest in, and it is certainly important. MM will show that it must be outranked by one other component of the tide, but it is a strong second.

This force is not resisted in any large amount by the ocean, since the water is relatively free to move tangentially. Ahead of this water is only other water until the curve ends, and then there is atmosphere. Both the water and the atmosphere are unconstrained to a large extent. The water has viscosity and pressure and the atmosphere has pressure, but other than that the force is free to act. The mass of the Earth is not behind the water at all to a significant depth, at this angle, so the freedom of the force to act is near perfect (compared to the radial force at the center of the circle of influence). The water can therefore develop a significant tangential speed.

Now, if we look just beyond the tangent—which is to say just beyond our circle of initial influence—we find water that has not been touched by any force at all. It is completely unaccelerated. As our accelerated water meets this unaccelerated water, it will pile up behind it, causing a swell. This is one of our high tides. In the initial stages of our analysis, it must be a complete circle of high tides, with a diameter on the curved surface of the Earth equal to 1/3 the circumference of the Earth. It will travel at some velocity around to the far side of the Earth, until blocked by a land mass or resisted by a reverse tide.

But let us return to our central force. MM has shown that it is radial and quite large, 572 times larger than any force we have yet had at our disposal in the history of tidal theory. It hits the Earth like a radial meteor, except that this meteor has a radius of 378,000km. It is like a meteor with a very low density. The main difference between our force from the Moon and a real meteor is that our force keeps arriving continuously. The Earth is hit by this low density meteor every dt, and it keeps getting hit without end. The waters are elastic, and they want to rebound from this force, but because it is continuous, they can do so only to a very limited degree. The freedom of motion is lateral, and so the waters move sideways to the force. Also, this lateral freedom of motion decreases with greater depth. As we go into deeper water, the freedom to move decreases in all directions simultaneously, which pushes the effect up and out on the surface even more quickly. This means that although the force is radial, the motion created is tangential. The water does not want to move down, and at greater depths it does not want to move sideways, either. So the result is motion sideways nearer the surface. Another circular wave is created, traveling out from the center. Initially this central wave is 60o behind the outer wave, and unless we show that it is moving faster than the outer wave, it will stay 60o behind it.

But which wave is bigger, the central wave or the outer wave? And what is the ratio? Already it is clear that they cannot be equal, since the mechanism of creation is so different, and this confirms what we know of tides. But to get a usable number we are going to have to do a mountain of math and mechanics yet.

But before examine how Spring and neap tides are caused by the Solar Wind, we have to look at one other major factor: the magnetic component of the field. Since with the central force we are looking at lateral results, we must remember that the magnetic field also works in this direction. So far all the forces MM has postulated and calculated have been electrical forces. But the E/M field has two components. By the right hand rule, if the electrical force is radial down, then the magnetic force will be clockwise, looking down on the ocean. Toward the center of our circle, this should have a magnifying effect on the electrical force, giving it the effect of a screw instead of a nail. This is true whether you imagine once big screw or billions of tiny screws. If the screws were impacting a solid, this would not be true regarding the tiny screws, but since we are dealing with a liquid, we have freedom of motion in all lateral directions, near the surface. The screws therefore cause a spreading, which magnifies the lateral forces already in play with the electrical field. The magnetic field and the electrical field work in tandem to produce the central wave.

Previously MM has shown that current tidal theory is a wash, so to speak. He showed that the barycenter is no part of the solution, that the tide differential math was pushed, and that the theory of heaping toward and away from the Moon was illogical. There is no possible cube law, as claimed, which destroys all the current math. This leaves the current data charts hanging. We have lots of good data, but no good way to fit it into a theory. Because we do not understand what is causing the data, our tidal predictions are not as good as they could be. Currently, all we can do is extrapolate data to make a prediction. Since the motions are consistent, this works pretty well. But it would be nice to understand what is causing the tides.

MM will show you again that it can't work, even without any math. Let us say that we accept that gravity is the cause of tides. We accept that the main action here is a pulling action from the Moon on the waters of the Earth. It is easy to see how this would create a heaping of waters under the Moon. It is less easy to see how this would create a heaping opposite. We are currently told that the opposite heaping is caused by the fact that the water over there feels less pull from the Moon, since the water is further away from the Moon than other water. But you have to be pretty careless to accept that at face value. Notice that they have just explained the two heaps by two different mechanisms. The near heap is caused by a straight pulling force. The far heap is caused by the differential field. In other words, it is caused by relative inequalities in the field. But just consider that explanation a bit more carefully. Gravity acts like an attractive force, in the same way as magnetism. So let us say the Moon is a big magnet, and the oceans are composed of iron shavings. The near heap is easy to imagine again. But is there any way to get a heap on the far side? With iron shavings, it may be possible, since the shavings that feel the least force move the least. There would be more iron shavings on the near side of the Earth than the far side, creating lower “oceans” on the far side, but there would be a smaller heap on the far side. This would appear to confirm current theory.

The problem is, water doesn't work that way. Water flows, remember? If we now make our iron shavings liquid iron, our far heap vanishes. This is because as liquid at the sides of the Earth is pulled to the near side, far side liquid moves to replace it. With any sort of liquid, what a pulling action would create is a near side heap and lower oceans everywhere else. Water cannot maintain a farside heap, since it would require friction to maintain it. Therefore, this explanation of the two diurnal tides is false. It cannot work in a liquid medium; especially a liquid like water, which flows so well.

Unfortunately, that can't work either, since the oceans are not orbiting the Earth. MM's critique on Newton's Proposition 66 was previously shown.

MM can give you another visual explanation, just as convincing. Again, we take the near heap as caused by gravity, a pulling force. But what if the Moon is above land? The Moon cannot heap waters when it is over land. The land masses on the Earth are quite large, and the Moon must physically pass over them in this heaping action. Let us say the Moon is directly above Minnesota. According to the current theory, we should have high tides all around North America, since the water wants to heap at Minnesota but can't get there. Since the distance is about equal, we should see about equal high tides at San Francisco, Boston, and New Orleans. Is that how tides work, in general? No, of course not. The current theory isn't even in the right ballpark. MM will show that current theory is once again mainly upside down or inverted. It is lower tides that are caused by the Moon traveling over land, not higher tides.

Yes, the (secondary) answer to the central question, “Why are there two main daily tides,” is “because there are two major land masses the Moon has to cross every day.” And therefore one of the reasons the two tides are not equal is because the Atlantic Ocean is not equal to the Pacific Ocean. As the Moon is crossing Asia, the tide has a chance to recede further than when the Moon is crossing the Americas.

You will say, “Gee, if that is true, it seems like someone would have seen it before you. It is not a very complex or esoteric theory, is it?” No, it isn't, but it requires that a theorist is looking at the problem in a certain way, and up to this time, historically, no one has been looking at the problem in that way. You see, if you start with the assumption that gravity is the main cause of tides, you are immediately lost. As we have seen, the gravity assumption pushes you into differential field equations, and once you start applying those equations like they did historically, you already have the appearance of the explanation of the two tides. So you never bother to even wonder if it might be the two main land masses or two main oceans that are causing some of the variations. It never comes up.

Now, MM has not read everything in history of course. Someone else has probably suggested something like this. But if they did, it is pretty well buried by now. And even if they did, it is very doubtful they were able to make it work. If someone suggested this before me, they likely tried to tie the idea to gravity somehow, since there has never been any other possible mechanism. But the only way to make the idea work is to tie it to the charge field, as MM has done in previous papers. MM has already shown that gravity has nothing to do with tides. MM has shown that the main tide is caused by a charge force from the Moon, and that this force is a repulsion, not an attraction. Beyond that, the spring and neap variations are caused by the Sun, but not by the Sun's gravity. They are caused by the Solar Wind conflicting with the charge force from the Moon to varying degrees. Here MM will show the more specific mechanisms of tide production, including daily and monthly variations.

We start by reversing the “heap.” There is no heaping. There is a depression, like a large bowl. If the Moon were over the middle of the Pacific Ocean, and you were in a boat right under the Moon, you would be at the center of a very large depression. Yes, this depression has a travel time to other locations, and the current model is not wholly wrong about the “age” of the tide in different locals. But in this case, when you are right under the Moon at sea, there is no lag time. If the Moon is directly above you, you are at the center of the depression. You are lower than the mean sea level (sea levels without a Moon), but the rest of the world is at high tide (or would be, minus time lags). This is because the mechanism of tide creation is relatively simple: when the Moon is over water, it creates a lower sea below it, and this forces all the other water higher. Just take a beach ball into the bathtub, press it down, and see the effect. It is precisely the same.

This mechanism is so much simpler and more logical than the current and historical mechanism. With gravity as the mechanism, we have to imagine a force transferred from Moon to Earth in some magical manner. In Newton's time, this magic was force at a distance. Now physicists pretend they have left that magic behind, but they haven't. They tell us gravity isn't a straight pulling force, it is a differential field. But you still have to have a mechanism to create the field. The field at the Earth is at a distance from the Moon, so how does the Moon transmit the information to the field? Current physicists hide in the math, pretending that math can somehow be the cause of itself, but it can't. That differential math has to be caused by some mechanism, and the mechanism is still lacking. That is why they are looking for gravitons. They tell you this problem isn't a problem, since it is a differential field, but when they are finished throwing dust in your face, they return to looking for gravitons. They do this because they know in their own minds that the Moon must be causing effects by some mechanism. The Moon cannot cause effects by free-floating math or by a list of harmonics.

My charge field solves this problem in one swoop, since we already have a mechanism for electro-magnetism. It is called the motion of particles, either ions, in the case of E/M, or photons, in the case of charge. We already know the Moon and Earth affect each other strongly electromagnetically. We have piles of data confirming it. And once you have defined the field as repulsive, as MM has, you have no problems with mechanics. All forces are caused by bombardment: by touch. It is real photons and ions that are pushing the sea down under the Moon. It is not magic or math, it is mechanics. Not only are you, in that boat in the middle of the ocean, in a real depression caused by real particles hitting you on the head, those particles are also making you weigh more.

Gravity also could never have been the cause since the gravitational forces are already balanced by the orbit of the Moon. The tangential velocity of the Moon is already said to balance the gravitational forces between the two bodies, so there is no leftover force to create tides. Forces that are balanced cannot at the same time be residual. They are either balanced, to create a stable orbit, or they are unbalanced, to create real pulls and motions. You cannot have both balance and motions caused by imbalance. The entire theory of tides via gravity has been highly illogical from the beginning.

Think of it this way: the Moon and Earth do not move at each other, right? The Moon stays at a pretty stable distance, and this is due to the balanced orbit. So, the Earth is not moving toward the Moon, as a whole, and it is not moving toward the Moon because the forces are balanced. If this is so, then why would the water move toward the Moon? Water would have to act differently than land, gravitationally, and we have zero evidence of that. In fact, we have huge amounts of well-accepted evidence that all matter responds the same to gravity. Therefore, the current theory is illogical, counter-intuitive, and falsified by all known data. The water cannot move more than the Earth as a whole, therefore the water cannot be heaped by gravity.

One will be told that the Earth as a whole is deformed by gravity, via Maclaurin's equations, and that the reason the water heaps more than the land is simply due to tensile strength. The land resists the pulling better than the water. But again, we have no evidence of that. Physicists still just assume it is true because the old equations tell them it is true. Because this heaping travels so quickly on the Earth, we have no way to measure it relative to the Moon, proving any given number is caused by heaping. But on the Moon, where tidal lock prevents heaps from traveling, we have very strong negative evidence. Gravity simply doesn't work that way. The Moon does not have crustal apsides pointing toward and away from the Earth. Not only is the Moon not oblate to any degree, with apsides pointing anywhere, if anything the Moon shows a negative tidal bulge on the front. That is, the nearside crust is not only not oblate, it is obliterated. The small inner Moons of Jupiter and Saturn also provide very strong and very obvious negative evidence. They are very near the planets and should be deformed strongly. But none are elongated radially like this. Current theory is a fairy tale on most levels. Not only is the theory threadbare (and contradictory) and the math fudged, the theory and math don't even match the most conspicuous data. That is precisely why the “tidal theory” page at Wikipedia is still such a joke. If they had a decent theory, they wouldn't hide it from you; but they don't have one.

Obviously, MM can explain the near depression on the Moon, since the Moon is being bombarded by the Earth. But MM can also explain things like the small tides in the Gulf of Mexico. Current theory tries to explain this as due to bathymetry, which is a fancy word for sea depth. It also points to the shape of coasts. These things have an effect, it is true, but they have missed the main reason the Gulf of Mexico has smaller tides. The reason is that the Moon has less land to cross over Central America. If low tide corresponds to “Moon over land” and high tide corresponds to “Moon over water,” then when the Moon only has to cross Panama, for instance, there is going to be very little difference between high tide and low tide. The tide won't have much time to go low before it has to go high again, which means the difference between maximum and minimum will be slight. MM has not studied the charts, but he would predict that the less land the Moon travels over, the lower the tides must be in that area. That is the primary reason the tides in the Gulf are small. The secondary reason is that the Gulf, because it is small and has an opening to the east, acts like a lake. The Moon is moving over the Gulf mainly east to west, and since the opening to the Atlantic is on the east, that is the way the tide will travel. The force from the Moon is down, and it acts to flatten everything beneath it over its entire radius. Therefore, when it is over the Gulf, it flattens the tide there. And the only release of energy is to the east. [See below for further clarification on how the Moon affects lakes]. The only tide that can be created in the Gulf is when the Moon is moving west off the coast of Africa, but even then the motion of the tide is mainly north and south, due to the pinching of the major continents. The Atlantic has much more freedom north/south than east/west, and so that is the way the tide tends to move.

This also explains the great variations in the Bay of Fundy. The greatest variations in that bay occur when the Moon takes its longest route over the Pacific and its longest route over Eurasia/Africa. This gives the waters the longest time to rise and the longest time to fall. The third major factor is lag time. The longer the delay, the greater the difference between maximum and minimum. In other words, if the Moon is traveling near the equator, it will cause a quicker response in those waters, lessening the effect of its long travel over Asia. But northern latitudes like Canada will be delayed, since the rise must travel from the equator up to that latitude. A later high tide is the same as a lower low tide, so the difference is maximized. The secondary cause of tidal differences is caused by the route of the Moon over land and sea, not by bathymetry or coastlines.

Therefore, a successful tide predictor would follow the route of the Moon. Since none of the current predicting machines measure the Moon's time over land, the harmonics are all garbage. They work (broadly and in general) only because they extrapolate from current data. It doesn't matter how you title or explain current data, as long as the numbers are good and are charted correctly. You can then push the data in extrapolation by weighting different lines in different ways, until the math matches the outcomes. You then have a “predictor.” But unless you can explain the mechanics beneath your harmonics, you only have a pushed table of data. That is what current charts are.

MM has no way of tracking the Moon over land and sea, but MM predicts that once MM's corrected mechanics is used, the tables of harmonics can be greatly simplified. For instance, by 1921 there were already 388 tidal harmonics published by Doodson. Now there are many more than that, though most of the newer ones are almost negligible. Only 62 numbers are really significant, and even many of those are not what you and MM would call significant. Not only are they not very significant in size, they aren't mechanically assigned. But even some of the largest harmonics are just given names, with only the flimsiest of theoretical assignments. If we just look at diurnal tides, for example, we find eight numbers applied to effects from the Moon, as in “smaller elliptic lunar diurnal” and “larger elliptic lunar diurnal.” If we go to NOAA to find explanations of these titles, we get nothing. We are taken to a page of “definitions”, but these definitions are just the titles themselves. If we dig we find that elliptic numbers are assigned to variations in the speed of the Moon, caused by its elliptical orbit. MM finds that assignment tenuous, because gravity has nothing to do with the speed of the object, or vice versa. It would be the slightly varying distance between Moon and Earth that would cause any effect, and that variation in distance could not show itself in a 24 hour period. The period of the elliptic lunar diurnals are about 24 hours. Even worse, the period of the larger elliptic lunar semi-diurnal is about 12.6 hours. The distance of the Moon from the Earth cannot change enough in 12 hours to create such a large effect. The larger elliptic lunar semi-diurnal is listed as order 3 by NOAA, which means it is a primary tide producer, the third largest known. Variations caused by an ellipse in 12 hours cannot do that. The Moon's eccentricity is low and it shows itself over a month, not over 12 hours.

MM thinks it is probable that the bulk of these harmonics are misnamed and mis-assigned. In fact, MM thinks they are all mis-assigned. This order 3 harmonic is most likely the Moon crossing the Indian ocean on some vectors and not others. And the higher order harmonics indicate the Moon crossing smaller landmasses like Cuba or the tip of India or Indonesia or the Philippines. Other harmonics would be created by the Moon crossing the Red Sea, the Bay of Bengal, etc. Once we combine all possible landmass vectors with all possible Solar Wind positions, we have a large number of harmonics. But these “harmonics” are all explained by four or five basic mechanisms, not by hundreds.

But before MM gets to these lesser harmonics, he needs to explain the primary harmonic. MM has said at least twice above that the landmass vector itself was secondary, so now is the time for me to tell you the primary cause of tidal variation. This will also be the cause of the two daily tides: the two humps on the semi-diurnal charts. These humps are currently explained by the two heaps caused by the force differential from the Moon, but MM has shown those heaps are a mathematical mirage. Tides are a charge phenomenon, not a gravitational phenomenon. The gravitational explanation has never been able to explain the variations, but the charge field allows for a pretty simple explanation of most of them. We start with the recognition that the Moon's daily apparent orbit around the Earth, caused by the rotation of the Earth, is inclined just like the Sun's orbit is inclined. That is, the Moon does not travel over the equator. The Sun travels on the ecliptic, and the Moon travels on an inclined path of its own. Now, we are told that the Moon travels west to east. Relative to the sky, it does so, but relative to the ground, it travels east to west, like the Sun. Both apparent motions are caused by the quick spin of the Earth. And it is this quick motion east to west by the Moon that we care about in tidal theory. We want to look at how the Moon physically travels over the landscape: we don't care how it travels relative to the stars.

So the Sun and Moon travel in the same apparent direction. But they don't have the same inclination. The inclination of the Sun is about 23.5 and the inclination of the Moon is about 5 more than that. So the circles they draw on the Earth will not only be in different places, they will be different sizes. Let us say that the Sun is at its maximum in the north, and so is the Moon. They will then draw the circles shown here.

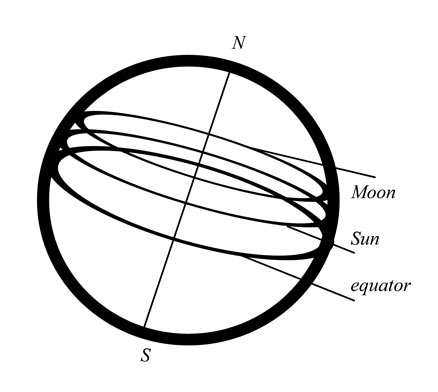
Let us look only at the lunar circle to start with. Here the Moon is furthest from the equator, so we would expect the greatest daily inequality. Why? Because the Earth is a dipole. The inequality is the different distance from north pole and south pole. Remember, the tide is a charge phenomenon, not a gravitational phenomenon, so we can now explain so much more. Think of the charge traveling to the north pole and back: that is one high tide. The charge traveling to the south pole and back is the other high tide. You will ask, “But why are they staggered? The crests are of different heights, which your theory now explains, but on the charts the crests are spaced evenly. Your theory doesn't explain that. In this position, the two tides would be off by only half; and when the Moon was over the equator your tides would be happening simultaneously, wouldn't they?” Good question. It is explained by the fact that the force arriving from the Moon is neither negative nor positive. It is photonic, not ionic, in the first instance. However, once it arrives, it must act by driving free ions. That is how the charge field becomes active in the E/M field. The photons drive ions. Therefore, since the oceans cannot be both positive and negative, the ions can go only one way. The tidal mechanism works in one main direction. And that means that if the tidal force is going south, it cannot also go north. It can get to the north pole only by going the long route—through the Earth. If the Moon is over the equator, it takes about twice as long on one route as on the other. If the Moon is not over the equator, it still takes roughly twice as long on one route as the other, but we get a small inequality. Remember, the input from the Moon is constant, so this is a continuous force we are talking about. We are not just turning it on. We are only explaining the stagger. The stagger is caused by the initial length of route difference, and then the stagger is maintained, like a current through a wire.

We now stack the landmass vector on top of this daily lunar vector, causing another semi-diurnal variation. This gives us the basic shape of M2. This is why M2 is variable itself. M2 has never before been resolvable, but explaining the tide as a charge phenomenon allows us to resolve M2 into its constituents. My proposed resolution is just a suggestion, but MM is confident that it is a suggestion in the right direction. Tidal theory must include the Earth as a dipole in order to bypass the historical blockade on progress.

Another charge variation will be explained by the variance of solar and lunar circles, as drawn in MM's diagram. Let us take just the solar circle, as drawn. Since the Sun is nearer the equator, compared to the Moon, its relative influence will be increased. For two reasons: 1) because the Sun is nearer the equator, the circle is bigger, which means the Sun is influencing a greater area on the Earth, 2) because the Sun is nearer the equator, it will be over the Pacific Ocean for longer than the Moon, increasing its tidal effect. Anytime the Sun is nearer the equator than the Moon, either in the northern hemisphere or the southern, the Sun's tide will be increased relative to the Moon's. On the other hand, when the Moon is nearer the equator than the Sun, the opposite will be true. However, in the southern hemisphere, this rule is slightly different. Part 1 of the rule will be the same. But with part 2 we must monitor the width of the oceans crossed. In general, we get less water as we go north and more water as we go south.

You will say, “Didn't you already explain the 46% variation using the Solar Wind, in part 2? It looks like you are giving us another variation here, by a totally different mechanism.” No, you have to understand that the 46% variation is just an average. That number is the expression of the overall difference between the Solar influence and the Lunar influence. But during any given month, that number fluctuates widely, depending on the positions of the Sun and Moon, and depending where you are measuring the tide on the Earth. Therefore, there are two major variations that requiring explaining. We are required to explain why the Lunar effect is greater as a monthly average, and also why the relationship between Sun and Moon varies so much. Current theory doesn't have nearly enough mechanical complexity. It has a huge amount of “harmonic” or data complexity, but very little mechanical complexity. My unified field allows us to propose many new sources of mechanics, as you see.

Another variation much better explained by MM's theory than gravitational theory is deep water variations. With tides caused by a pull, these variations are pretty much impossible to explain mechanically. Not only is any pull mechanically impossible, but without a particulate field, it is a joke. With the mechanism as a push—charge bombardment—deep water variations are explained as compression waves. According to current theory, tidal waves are shallow water waves. But we know that isn't true just from looking at the data charts. Many of the nodes on the TOPEX/Poseidon chart are in very deep water. By incorporating E/M theory, and wave production as a push rather than a pull, we simply let the wave travel to the ocean floor and bounce back. It is easy to keep the theory mechanical this way.

Another major “harmonic” the current theory utterly ignores (at least MM does not see it in the charts) is backwash. Tides generally get larger with increasing distance from the equator, and this is especially true in the north Atlantic, although it is also true in the North Pacific (Alaska, for instance). By MM's mechanism, this would be caused by backwash. In other words, the tide has to travel up or down from the path of the Moon. But in the north, the tide cannot disperse. It is squeezed by landmasses and ice. It can only go up to the arctic circle and reverse. This basically doubles the high tide in northern latitudes, and the effect is greater in the Atlantic than the Pacific because the Atlantic is squeezed more. The Pacific has much more room to divert this northern tension by releasing it to the south. In the south, the oceans all connect. There is no bottling up of waters. This is why tides are generally low in the southern hemisphere. Only local bottlenecks like New Zealand and Cape Horn create tides there.

In this way, the current table of harmonics is little more than a list of bad titles. It is a compilation of every bad theory of the past, from the bulges of Maclaurin to the shallow water variations of Laplace. The lunar and solar names aren't even used consistently, since we find that in the diurnal charts, for instance, the periods are either around 24 hours or around 27 hours. Obviously, those periods near 24 hours should be assigned to the Sun, and the others are probably lunar. And yet, the main lunar diurnal, which has a period of 23.93, is assigned to the Moon. We also never get any theory about what causes the lunar diurnal. It is listed as separate from the lunar semi-diurnal, so MM supposes it must have a separate cause. What bulge causes the lunar diurnal, and how is this bulge created? How can one Moon create so many bulges via gravity?

Finally, MM will show you another failure of current theory, and another explanation of mine. If the Moon creates tides by a heaping effect, then it may be asked why, when the Moon crosses a large lake like Lake Victoria in Africa, it does not vacuum the lake up into the sky, or at least heap it noticeably. If the Moon is powerful enough to raise the levels of all the oceans, it should be powerful enough to effect one lake. And yet Lake Victoria is famous for its lack of tides and currents. Very damning evidence against current theory. But the tables will be turned on me, and the same question will be asked of MM's theory. The Moon, when passing over the lake, should blast it out of its boundaries, sending the coastal waters many meters higher. Why don't we see this? Once again, the answer is simple: the depression caused by the Moon is much larger than any lake. Lake Victoria is the perfect example to look at, not only because it is near the equator, and must be passed over by the Moon, but because it is the largest lake in the world by area (if you take Huron and Michigan as separate lakes). Therefore, if Lake Victoria is unaffected by a direct pass of the Moon, then no lake can be affected. Think of it this way: remember MM's analogy to a beach ball being pressed into a bathtub's water? Well, what happens if your beach ball is larger than your bathtub? The water can't move. The water, and all the land around, will be given extra pressure, but no motion will result. This is why Lake Victoria is unaffected by a pass of the Moon. It is precisely because the lake is near the equator that it shows no tides. Even when the Moon misses it, the Moon is passing near enough that the lake is still entirely within the Moon's depression.

And this is why the Great Lakes do experience small tides. The Moon never goes that far north, so the Moon never passes over the Great Lakes directly. When they experience small tides, they are in caught in the edge of the large depression of the Moon. So we would expect the first tides to be moving north, followed by tides moving south, to bring the water back. This is in fact what is seen. The tides in the Great Lakes move north and south. This is how they are separated from other currents. For instance, the currents in Lake Erie would be expected to flow west/east, since that is the main motion of the waters to the St. Lawrence. If the tides also moved west/east, they would be undetectable, but many have detected small tides in Lake Erie. We are told that Erie and Superior have the greatest tides*, but that should be restated: Superior and Erie have the mostly easily detected tides, since they run east/west. The currents in Michigan and Huron run north/south, so they can't be separated from lunar tides. And we may assume that Lake Ontario can dissipate any tide directly into the St. Lawrence.

MM showed the size of the Moon's arriving force visually in part 1, with the illustration showing the emission of the Moon expanding as it moved from Moon to Earth. We simply increase the surface area in a straightforward manner, with distance. The circle of emission from the Moon is 60 times larger than the Earth itself at impact, so the depression is quite large. MM estimated that the width of the depression was 1/3 the circumference of the Earth, although this number was more a measure of the influence of the charge at any one time than a true measure of the depression itself. Since the strength of the force is relatively small over any small area, the depth of penetration is small, even at the center, so that the depression doesn't act like a rigid bowl. If it did, the center of the bowl would penetrate the mantle. In other words, our beach ball deforms as it presses into the bath water. In the case of the force from the Moon, it goes from being convex to being concave, spreading out across the surface of the sphere.

At any rate, this is all just to show that the force from the Moon arrives over a very large area, too large to create a tide in Lake Victoria. MM would suggest that the pressure increase would be measurable, however, and an interesting experiment would be to monitor the water pressure of the lake during a pass of the Moon directly overhead. MM suspects that the change would be significant. MM would also question the natives, seeking stories of “supernatural” phenomena observed during passes of the Moon directly overhead. Effects on fish and other animals, for instance. These stories might provide a clue of where to look for more evidence.

(*1)For other phenomema that follow these cycles, you may read this interesting paper from sciencedirect.com. They assume, without any evidence, that these cycles follow gravity, but MM has shown in a series of papers that these kinds of cycles follow charge. Gravity has no mechanism to cause these cycles, while charge does.

(*2)The tangential velocity of an old satellite is caused by the magnetic field working at a right angle to the electrical field. The electrical field causes the orbital radius and the magnetic field causes the orbital velocity. Only very young satellites can be retrograde, and therefore retain a large part of their "innate" velocity.

(*3)Once the E/M field reaches the ocean, it can no longer travel at speed c, since it is then conducted by the water. So the time period is determined, in part, by the speed of electricity in saltwater. From the other end, the time period is determined by the gravitational acceleration of the Earth. While the E/M field disturbance from the Moon is racing through the water, the Earth is accelerating outward at 9.81m/s2. So, in effect, the tangent of the Earth is changing while the effect is moving from center to tangent. If the Earth was not expanding, the tangent would be near the top of the Earth in the diagram, and we would find nearly half the Earth hit by the sphere arriving from the Moon. That is, x in our equations would be nearly r. Knowing this, we can solve from the other end. We don’t have to ask how long it takes electricity to travel 1/6 the circumference of the Earth, on the surface of oceans; it is easier to calculate how long it takes the Earth to expand from r=5524 to r=6378. Since both times are equal (the period t is determined by when the two motions meet) we choose to do the easier math. At 9.81m/s2, it takes the Earth about 13.2s to expand 854km. Therefore, we may assume it takes electricity about that long to travel the given distance. So t=13.2s, the time for one complete "wave" of disturbances to arrive from the Moon. Velocity of E/M field in seawater=506km/s.