Miles Mathis: Spring and neap tides are caused by the Solar Wind

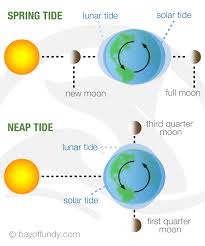
As a follow on from the Miles Mathis paper: (Tides are caused by E/M field not Gravity, MM will now propose a mechanical solution to spring and neap tides that does not include the Sun.

In this previous paper, MM stated that the Sun's effect on tides is not caused by the Sun's gravitational or E/M fields. Both are too small at the distance of the Earth to cause the size of the variation we see. Even if gravity were the pulling force, or the equivalent of a pulling force, there is no way to get two spring tides every month of the size we see.

The accepted scientific view is that spring tides are explained by an alignment of the Moon and Sun. There are roughly two alignments each month, of course, one in conjunction and one in opposition. If we treat gravity as a direct pulling force, neither the vectors nor the numbers work out. Clearly, the Sun cannot add itself to the Moon's force in the same way in opposition and conjunction. To answer this obvious problem, the tidal field is now treated as a differential field. This creates tides both front and back, from both Sun and Moon. At first glance this appears to work. But a closer analysis shows that the numbers don't add up.

In order to get the necessary 46% solar tide, the standard model fudges the math, applying the same equation to solar and lunar tide. Unfortunately, the Earth is not orbiting the Moon, so the equations can't be the same.

The barycenter solution is a necessary outcome of current gravitational theory, but it would swamp both solar and lunar tides and clearly all spring and neap variation. Neither the differential field nor gravity as a direct pulling force can explain tides.

What really causes the spring and neap tide variation is the Solar Wind. The basic electromagnetic field of the Sun is 15 times smaller than the Lunar field at the distance of the Earth, but the Sun has many electromagnetic effects that are caused not by the standard radiation of all matter, but as by-products of fusion. This is already well-known. The Solar Wind is powerful and mostly uni-directional (radial out from the Sun). This makes it the perfect candidate for spring and neap tide variation. But to even consider it as a candidate, you first have to be explaining tides as an electromagnetic phenomenon. Since no one else is doing that, no one else is anywhere near the true solution.

The quickest way to show this is at neap tide. At neap tide the Sun and Moon are orthogonal. That means the Solar Wind will be blowing at a 90^o angle to either of the two opposite lunar positions. In the previous paper on tides, it was shown that the tidal mechanism is both electric and magnetic, and in the two neap positions, the Solar Wind is at the perfect angle to obliterate the magnetic component of the tide. The magnetic component is orthogonal to the electrical force, and in this position, the Solar Wind is also orthogonal. The Solar Wind therefore has little or no effect on the electrical component of the neap tidal force, but it interferes with the magnetic component to a very large degree.

In the spring tide positions, we have a different encounter with the Solar Wind. When Moon and Sun are on the same side, the Solar Wind has little effect on the magnetic component, but it would be expected to augment the electric component. When the Sun and Moon are in opposition, the magnetic component is once again little affected, but the electric component would be expected to be diminished. That is, it would be expected to be diminished, except that the E/M field is shielded from the Solar Wind in that position. We would therefore expect a small diminishment only. Most of the effect of the Solar Wind will be blocked by the Earth.

You will say that the Solar Wind must be blocked by the Moon, when Moon and Sun are on the same side. And to a small degree, this is true. But because the Moon is much smaller than the Earth, the blocking is much greater when the roles are reversed. When the Moon and Sun are in conjunction, relatively little blocking takes place. The greatest effect would be in total eclipse, of course, but the Moon doesn't hit that position very often, and it never hits it for the entire Earth. For this reason alone, the Moon cannot be expected to be a good blocker of the Solar Wind.

Now you will say that the magnetosphere of the Earth blocks the Solar Wind at all times, since if it didn’t we would be fried by Solar radiation. Once again, this is true to a degree. The Earth’s magnetosphere does block a part of the Solar Wind. But it does not block it all, or we would not have the Aurora Borealis and all the other known effects. There is a significant year-round effect even with the partial blocking, and this is important since we need the effect to be consistent in all positions.

In fact, even if the magnetosphere were proved to block all direct Solar Wind effects from reaching the surface of the Earth, we could still use it as part of my tidal theory. The reason for this is that we do not need a huge number of ions actually hitting the oceans' surfaces in order to use the Solar Wind in the equation. The very fact that the magnetosphere blocks the Solar Wind is proof that the E/M field of the Earth is greatly affected by it. The energy that the field expends resisting the Solar Wind is energy it can't use in that position to create tides. The field at any dt is a limited field of energy, and if field strength has to be used in the upper atmosphere, say, to deflect ions from the Sun, then that much field strength must be subtracted from the field as a whole. So the tidal effect is the same whether the ions are deflected in the upper atmosphere or whether they make it to the ocean’s surface and deflect some electron there.

The next problem concerns the ions themselves since the Solar Wind is composed of both positive and negative ions. However, the main effect is on the magnetic part of the field, when the Moon is orthogonal to the Sun. In those positions, the Solar Wind acts like cross traffic in the field. As MM has shown in another paper, cross traffic impedes the motion of the field, no matter which direction the cross traffic is. Which is as much to say that both positive and negative ions will have the effect of impedance on the total tidal force in those positions. This is even easier to understand and accept if you follow the reasoning of the previous paragraph. If the E/M field of the Earth/Moon is being diminished in those positions by its role in having to block the Solar Wind, then that diminishment is absolute: it does not depend on the charge of the Wind at specific points. In other words, the total E/M field of the Earth/Moon does not lose when it blocks positive ions and gain when it blocks negative ions. It loses either way, since the total field strength is a matter of total potential. The Solar Wind will sap field potential either by interacting with positive or negative parts of the field.

One more way to show this is to point out that although the Earth's magnetosphere may block the Solar Wind, and although the Moon’s magnetosphere may do likewise, the E/M field of the Earth/Moon—which only together causes tides—spreads across the entire distance from Earth to Moon. The greatest effects of the Solar Wind will be at neap tide, and at neap tide the Moon is orthogonal to the Earth, compared to the Sun. In this position, the E/M field of the Earth/Moon is highly exposed. It is literally out in the breeze. The magnetospheres of the Earth and Moon cannot protect the midmost points of the combined field, and it is here that much of the brunt of the Solar Wind will be felt.

Now let us look at the force of the Solar Wind.
The speed of the wind averages about 500 km/s near the Earth.
The mass is 10⁹ kg/s.

But we need a density and a flux at 1AU:
D/s = 10⁹ kg//s4π(1AU)³/3 = 7 x 10^-17 kg/skm³
Φ = 3.5 x 10^-14 kg/s²km²

If we express mass as m³/s², we obtain
Φ = 3.5 x 10^-20 m/s⁴
a = √Φ = 1.87 x 10^-10 m/s²

Now we compare this to the force from the Moon, calculated in Part 1, which was a = 4.7 x 10^-10 m/s². We have found that the force from the Solar Wind is about 40% of the force from the Moon. The standard model finds it needs the effect from the Sun to be 46% of the effect from the Moon, so we are close to that already, with only the first rough equations completed.

Treating the mass as a 3D acceleration above, which allows MM to use the square root of the flux for the "field acceleration", MM now takes a pretty little mathematical shortcut in comparing an E/M radiation field to an ion radiation field. The Earth/Moon field is a field composed of E/M photons, which are treated as massless. But the Solar Wind is a field of ions, which are far from massless compared to the photons. Therefore the ion field acceleration has to include the acceleration due to mass on the ions. It is automatically included any time the kilogram variable is used, so all MM has to do is to remember that, and use it in his equation. Seen this way, the flux is then an acceleration of an acceleration, which is why we get the s⁴ in the denominator.

It might be thought that the acceleration due to the average mass of the ions should be subtracted from the flux. We can just take the square root because the mass of the ions determines all the other variables in this field. Look at the variables: flux is determined by density and velocity, and both velocity and density are determined by the mass of the ions. If they weighed more, the field would accelerate them less, and the velocity would drop. You can see that the question above could be stated, "why should the acceleration due to mass equal the acceleration due to the field?" Because, MM has shown that they are the same thing. Gravity and mass are the same thing, stated in different ways. The "field" that is accelerating the ions is a field defined by the mass of the Sun and the masses of the ions. The mass of the ions determines both the acceleration due to mass, which is the gravitational expansion of the ions, and the motion in the greater field. Therefore the flux in this case can just be written as the expansion of the ion squared.

So the short answer is, the ions are moving as they do because of a gravitational field. A gravitational field is exactly the same thing as a mass field, except that one is expressed as motion and one is expressed as force in collision. If the motion in question is caused only by gravity, then a total potential force in collision is just the mass squared, expressed as acceleration. You can see that this gives us an easy way to calculate force even though we are only given a velocity.

So, we now have 40%, but we need 46%. Fortunately, we can now bring in the E/M acceleration from the Sun, calculated in Tides are caused by E/M field not Gravity, and add it to the Solar Wind. It provides precisely the extra 6%.

1.87 x 10^-10 m/s² + 3.13 x 10^-11 m/s² = 2.18 x 10^-10 m/s²
2.18 x 10^-10 m/s²/4.7 x 10^-10 m/s² = 46.4%

The acceleration from the Sun is two phenomena stacked: the Sun's charge field and the Solar Wind. Since the two phenomena are caused separately, we can stack them in effect. The Solar Wind is an ionic field, and the ions are caused by nuclear reactions. The charge field, however, is a fundamental field, independent of the ionic field, being simply a field of charge photons. Jupiter, for instance, has a charge field, but Jupiter does not have a planetary wind like the Sun's wind. For this reason, we can add the two types of E/M fields from the Sun.