The Double Slit Experiment is a Chimera

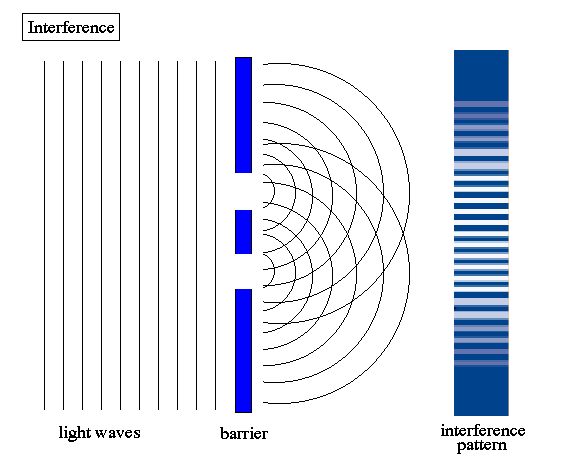
First posted August 25, 2008 In this paper Miles Mathis will show the simple mechanical solution to the famous double slit (or two slit) experiment. Feynman called it the most important experiment for understanding quantum motion, and he may have been right. The most difficult problems are always the most important, and this one has remained unsolved up to this minute. Thomas Young first performed it in 1801, which means it has been a mystery for over 200 years. Even Feynman failed to solve it. He offered a mathematical solution only, but was not able to provide a physical solution.

MM will solve the two biggest problems here: the problem of the single photon and the problem of the detector. In the first problem, we let photons go through the experiment one at a time. Using the photon-as-particle theory that Einstein proved and Feynman confirmed, we expect no wave interference, since the photon must go through one slit or the other. But we see interference. The single photon seems to be interfering with itself in some strange way. Up till now, there have been several proposed solutions. Wikipedia lists the most important. The first they mention is that the “wave front” of the photon goes through both slits and interferes with itself. Since the wave front is still not defined mechanically, this solution is not very compelling. The wave front is and always has been defined using Huygen’s visualization. The wave is seen as a semi-circular forward transmission from every point on a line of moving photons. With a single photon, this would be a semi-circle in front of the photon. But we are never told how far this semi-circle extends, what it is composed of, or how it acts upon the field. So we will let this explanation pass as wholly unsatisfactory.

Another solution is to define the photon as a probability. A discrete particle cannot go through both slits at once, but a particle as probability can (as long as we define probabilities in certain ways).

The third and currently accepted explanation is an extension of this second one. Feynman proposed that the photon-as-probability traveled every possible path, and therefore through both slits. Each path is given an equation, and we “sum over” all these equations. If we sum over in the correct way, we achieve interference.

Now, admittedly this is a clever mathematical solution. Feynman was a master of clever mathematical solutions, and this is one of his best. Mathematically it works. But it is not a physical or mechanical solution. It is a mathematical solution. Feynman was not so much a physicist as he was a mathematician that had invaded the physics department (the same could be said of most modern physicists). In his own way, Feynman admitted this. He did not admit to being an invader, but he admitted that his solution was only mathematical. He knew as well as anyone that it was not physical, by the old definition of physics. He got around this by claiming that new physics was and must be mathematical only, since there was no possible mechanical solution.

He was wrong, as MM will prove very quickly. His math works precisely because there is a physical reality underlying his probabilities. Probabilities are not the causa sui, the cause of themselves. It is illogical—even as a piece of mathematics—to propose that probabilities are spontaneously generated, or that they are primary generators. No, they must be generated by a real field. Even in pure mathematics, probabilities are always secondary numbers, produced by an underlying field of numbers. A field of probabilities cannot be a foundational field. They therefore cannot take the place of a physical field.

What foundational field of numbers is creating the probabilities in this experiment? The answer is: the foundational E/M field. In every analysis of this problem and this experiment to date, the analysts have over-simplified the problem. They have assumed, without even putting the assumption into words, that the experiment is taking place in a sort of void or vacuum. The only things they look at are the slits and the photons. But the slits and the photons are not the only important players in this field. Even if you ran this experiment in a vacuum, with the walls and the photons as the only objects in the vacuum chamber, you would still not have a void, since the walls are still material objects. As such, they must be emitting an E/M field. The wall, even in a vacuum, is radiating a field all the time. It is this field that the photon must move through.

MM has proved in several previous papers that the charge field, if defined mechanically, must have mass equivalence. If it has mass equivalence, it must have materiality. In other words, the field that mediates the charge between proton and electron must be made up of discrete particles itself. What is now called the messenger photon cannot be a virtual particle with no mass or energy. It must be a real particle and create a real field. In Coulomb's equation is a Unified Field equation in disguise: Charge at the Quantum Level MM has already given this messenger photon a new name (the B-photon) and a definite radius (G times the hydrogen radius), so it makes sense to use this particle to explain the two slit experiment. This field is not a virtual field, a summed-over field, or an ad hoc field, but a physical one mathematically derived from its place in Newton’s gravitational equation.

This being so, we must now recognize that our central wall in the two slit experiment must be radiating this field (MM is talking about the wall drawn in blue above, which contains the two slits). Our single photon must be moving through this field emitted by the central wall. This changes everything in regard to the experiment. The first thing to notice is that we have interference patterns set up by the slits even before the single photon is emitted. If we know that every atom in the wall is emitting this field, as a simple bombarding field, the two slits will create an interference pattern in the field without a single particle moving through the field. The interference patterns are already there! The single photon does not create them. The probabilities do not create them. Karl Popper’s “propensities” do not create them. The real atoms in the wall create the interference pattern, with simple spherical emission.

The only problem is that we cannot “see” this field. It does not create any lines in the far wall, since B-photons are not the same size or energy as the single photon we put through the device. Our far wall is chosen because it is made of a material that reacts when the single photons (or electrons, or whatever particles we are using) hit it. But it does not react to the foundational E/M field. It does not react to B-photon radiation. This field therefore remains invisible to us. We do not “see” the interference patterns until a large enough particle moves through the field. The motion of this particle through the field and its reaction to the far wall give us our only data. The experiment is not set up to give us any data about the B-photon field, except indirectly.

It is true that the B-photon field does not create exactly the same patterns as the series of single photons. If we want to be very rigorous, we can actually draw the field set up by the B-photons and the two slits, and find the interference nodes of that foundational field. Then we let the single photons go through field, and we see how they must be funneled through that field, by direct contact with the B-photons. This funneling creates a second, dependent field. Both fields will have a definite pattern, completely determined by the primary emission, but the secondary pattern will not be equivalent to the primary pattern, for what MM thinks are obvious reasons.

This simple mechanical explanation not only solves the single photon problem, it also shows why different particles are affected in different ways by the same field. It is quite easy to see that an electron will be funneled by this B-photon field in a different manner than a photon, due only to the size difference. If the photon is like a baseball moving through a field of golf balls, the electron will be like a bowling ball moving through a field of golf balls. Put simply, the electron will be funneled much less efficiently. It will resist the field more successfully, and the field will be upset by its presence to a greater degree. All this will now be visualizable, predictable, and mechanically transparent, due only to the discovery of the pre-existing interference pattern and the real field that creates it.

Now let us look at the mystery of the detector. It has been found that putting a counter or detector in either slit changes the entire data in ways that are not predictable with current mechanics. Specifically, a detector in one slit will destroy the entire interference pattern, returning us to a single pattern on the far wall. The current explanations for this are even more tenuous than explanations for the single photon, since Feynman’s sum-over trick does not explain it. Attempts to fudge an answer by claiming that we must now sum-over both before and after the detector do not answer the problem unless it is shown how the detector changes the total path. No one has yet done this. Unless Feynman can show why AB + BC is not equal to AC (with the detector at point B), he cannot develop an equation for AC that is different from the case without the detector, and therefore cannot show a sum-over variance. Feynman never claimed to any physical knowledge of the two slit experiment, therefore his math does nothing to solve the detector mystery.

The detector mystery has led to even more absurd solutions than the single photon mystery. Along with entanglement, the detector mystery has been one of the primary causes of neo-idealism in physics. Many physicists now believe that simply wanting to know something changes the entire experimental set-up, as if asking a question can physically interrupt a field. In this way, physics has crossed over into mysticism. For what MM will show are the flimsiest of reasons, physics has chosen to accept spooky forces and ideational interference in their experiments. Rather than continue to look for mechanical explanations, they have preferred to be satisfied with magic (See my paper The Probability Wave of QM is not reality).

But, again, the real solution is simple and logical and mechanical. The detector is a device with real size and materiality. It inhabits space in or near the slit. This detector creates a real field of its own. If it did not, it could not detect anything. Wikipedia says,

The detection of a photon involves a physical interaction between the photon and the detector of the sort that physically changes the detector. (If nothing changed in the detector, it would not detect anything.)

Logically this is true, but it fails to describe the correct interaction. It is not the interaction between the photon and the detector that deletes the interference pattern, it is the interaction between the field created by the wall and the field created by the detector. The field of the wall is a B-photon field, which is made up of exceedingly tiny particles. The field of the detector, whatever it is, must trump this field. We do not have detectors that make use of the B-photon field, since, up to now, we have not been aware of it. All our detectors use “larger” fields, since these are the only fields we can create and use. To use the ball analogy again: if the B-photon field is a field mediated by golf balls, the field used by our detector to detect the particle passing through the slit must be made up of baseballs or bowling balls. This detector field is obviously going to destroy the golf ball field and all patterns in it. Our particle passing through the slit is then going to be funneled by the detector field only. This detector field does not create an interference field, so we do not see one.

MM will now make a prediction that will prove that my solution is correct. Look at the illustration at the top of this article. We have two walls, both in blue. Let us simply add a third wall on the left side of the illustration. This is the direction the particles are projected from. We will house our projector in a wall. Like the wall on the far right, this wall on the far left will be made of a substance that allows us to mark a hit by a photon or other particle. As for the central wall, we will make it reflective on the side near the projector (without changing its makeup in any other way). We simply want to be sure that, in the case our particle does not go through one of the slits, it bounces back and returns to the first wall. We don't want the central wall to absorb our particle. OK, now for the prediction. If we purposely fire our particle so that it fails to go through either slit, and it hits the central wall and reflects, MM predicts that we will find the same interference pattern on the near wall that we found on the far wall. Given the current explanation of Feynman and others, there is no way this could be true. We have no particles going through slits, therefore no sum-over solution will explain the interference. But my solution accounts for it in a very straightforward way. In my solution, it is the central wall that is creating the initial interference pattern, and due to the position of the central wall, it must be creating the same pattern both backwards and forwards. This being true, we must find a very similar pattern created on the near wall to what we found on the far wall. It may not be identical, since reflection will create angles not found when the particles went through the slits. But we would expect a similar interference pattern to be created nonetheless, since the same underlying interference pattern is funneling the particles in both instances.

You will say that the first and third walls must also be emitting my B-photon field, supposing it exists, and that this must skew my solution. But this is not true. The near and far walls are emitting that field in a linear way, since they do not contain any gaps. Only the central wall is emitting an interfering field, due to its shape. Since all the emitted fields are real, they must interfere with each other in some way, and to some extent. But since the far wall is emitting a rectilinear field, or its equivalent, it will not change the shape of the fields from the central wall. It may tamp them down a bit, as a matter of total energy, but it would not be expected to destroy the curves.

The only real problem in the set-up MM has described is the hole in the first wall created by the projector itself. This hole will create a ripple in the B-photon field emitted by that wall. MM thinks this factor could be removed from the experiment by setting our projector above the first wall, instead of in it. Then all we have to do is calculate the proper reflection angle, so that particles reflected from the second wall are sure to hit the first wall. B-photon emission from the body of the projector itself will still disturb the fields set up by the walls, but perhaps this can be minimized in other ways. Even if the effect of the projector cannot be removed from the experiment, we will still find patterns created on the near side that cannot be explained by Feynman or the current model. Even if the first wall continues to emit like a single slit wall, no matter what we do, we will still find the near field acting like the sum of a single wave meeting a double wave. My method allows us to calculate and predict this field. The current solution cannot predict or explain these patterns at all.

Speaking of prediction, my solution revitalizes Laplace's famous god's-eye view of mechanics. Laplace proposed that an omniscient entity, knowing an initial state of the universe, could predict all final states. MM does not actually agree with Laplace's theory, but the reason he disagrees has nothing to do with mechanics. Applied strictly to mechanics, MM thinks his theory is a good one, since it forces us to seek a deterministic and mechanical solution before falling back on a non-deterministic and non-mechanical solution. In physics, this tends to keep us honest. MM also thinks that all these QED arguments against Laplace in the 20th century must ultimately fail. As MM has shown here, QED is failing to make good predictions not because the quantum world is fundamentally unpredictable, but because the mechanical groundwork of QED (where it exists at all) is incomplete and false.