Entanglement: 'Spooky action at a distance' is not real

Wikipedia defines "Entanglement as follows: "Quantum mechanics holds that states such as spin are indeterminate until such time as some physical intervention is made to measure the spin of the object in question. It is equally likely that any given particle will be observed to be spin-up as that it will be spin-down. Measuring any number of particles will result in an unpredictable series of measures that will tend more and more closely to half up and half down. However, if this experiment is done with entangled particles the results are quite different. When two members of an entangled pair are measured, one will always be spin-up and the other will be spin-down. The distance between the two particles is irrelevant."

A close reading of those few sentences already shows how the mystery of entanglement is a manufactured mystery, created by false probability assumptions. The problem in this Wiki quote is closely related to Schrodinger's cat mystery. In a thought problem, Schrodinger put a cat in a box and then assigned a probability number to the cat: say, .5 the cat was alive, .5 the cat was dead. We can't see the cat, so we don't know. Quantum mechanics says the numbers are all we know. Schrodinger says no, there is some fact underneath the numbers: either the cat is dead or it is alive. When we open the box, it must be one or the other, not both. Amazingly, the princes of QM did not say, “Yes, well of course. But we don't know until we open the box.” That would have been sensible. No, QM said to Schrodinger that the cat was NOT really alive or dead. It was neither alive nor dead until we opened the box and saw it!

Because Schrodinger lost that argument, contemporary physicists actually believe that the “physical intervention” of measurement determines part of the math. It does this via the HUP, the Heisenberg Uncertainty Principle. A certain interpretation of the HUP makes the physicist an actual part of every equation, and this interpretation is now the accepted one. That is spooky enough, in itself, but entanglement is even spookier. Using the anti-Schrodinger interpretation of cats, QM had decided that nothing could be known about particles except their probabilities. In other words, there was no certain knowledge beneath the numbers. But with entanglement, we get certain knowledge from probabilistic situations. With entangled particles, “one will always be spin up and the other will be spin down.” Note the word always. That is certain knowledge.

To explain this, quantum physicists have come up with the idea that the particles are in contact with each other over huge distances, without any mediating field or particle. Yes, they can talk to each other instantly, so that when the physicist measures one as spin up, the other can flip immediately to spin down to conserve parity.

All this is patently absurd, but neither the physicists nor the philosophers can seem to cut through to the fairly obvious answer. They can't do that because they have made the question much more complex than it is. First of all, the physicists have buried the problem under decades of math and terms. Then the philosophers have followed, adding their mountain of semantics and lingo and sloppy thinking. One must come to the conclusion that neither the physicists nor the philosophers want a simple answer. They only want to look smart, bandying a vast vocabulary and an infinite disrespect for their readers.

The fairly obvious answer is that their first postulate was wrong. They assumed that there was no reality under the probability numbers, but entanglement showed that there was. Just look at the Wiki quote again: the whole problem is between their postulate and the outcome of the experiment. Faced with a contrary experimental outcome, a sensible person would admit his postulate was wrong, but that is not the way of modern physics. Physicists cannot admit they were wrong. So, in order to keep their postulate, they stoop to this 'spooky action at a distance' magic.

The physicists claim that non-locality is force at a distance, which puts physicists right back with Newton. Ironically, Feynman did not believe in this force-at-a-distance dodge. In his book QED, Feynman explains partial reflection by glass by assigning an arrow and a clock to each individual photon. MM has shown that the arrow is a vector and the clock is a spin. The clock and arrow, taken together, are able to tell us where in its spin cycle each photon is. In other words, we can calculate where the particle is in its own wave. Strangely, his method would have allowed him to explain entanglement without force at a distance, which would contradict the assumption that states such as spin are indeterminate, but he never said so.

Following his logic: since each photon has both a turning clock and a vector, each photon has both a wave motion and a linear motion. This means that the wave belongs to each photon, not to the set of photons. This is revolutionary because, in this way, light is no longer analogous to sound: it is not a field wave, but a particle with spin.

The wave belongs to each particle, and may be assigned to a mechanical motion: spin. If each photon has a real spin with a real wavelength and a real period of rotation, then we can use that period of rotation to track it. Using Feynman's little turning clock, we can follow the photon, no matter how far it travels, and predict with some certainty what state it will be in.

We cannot say that the clock will be at 6 or 12, but, given an initial state, we can predict a final state. If the clock was initially at 12, after some time we can predict that the clock will be at 12 again. To do this, we only need to know the period of rotation and the time of travel. If we know the wavelength, we can calculate the period of rotation quite easily, so this is not a difficult problem mathematically. Once we sort through the mechanics, the math becomes simple.

This explains entanglement because we do know an initial state. We don't know if the quanta are at 12 or 6 on the clock face, but we might know one is opposite the other, for example. If one is at 6, the other is at 12. If they have the same periods of rotation, then after any time, they will still be opposite, without any communication between them. Other relationships will also be trackable and stable, as long as the periods of rotation are known relative to each other. In other words, as long as we know sizes and wavelengths, we can predict comparative wave positions at any distance or time away from collision.

This is the mechanical explanation of entanglement, without spooky forces. Albert and Bell have both been proven wrong, by direct demonstration.

The Unveiling of the CHSH Bell tests

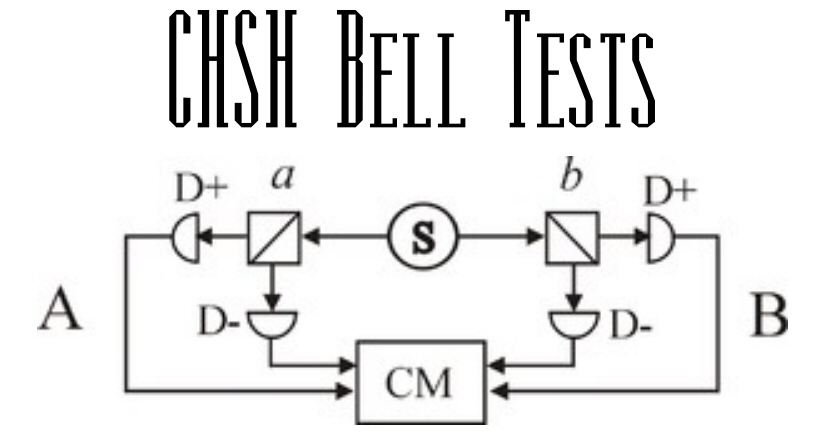
In previous papers MM has shown the flaws in Superposition is not Mystical , and square polarizer experiments. Here MM extends that analysis to include the CHSH Bell tests.

When MM says he has shown the flaws in these previous experiments, he does not mean hat he has shown some theoretical or experimental problems, such as loopholes or operational flaws. MM has not claimed to have found that hidden variables are still possible . No, he has assigned the actual variables to the photons, then run them through the machines, showing how they match the results without quantum mechanical assumptions of entanglement. This falsifies entanglement and the current theory in the most direct way possible. MM has proved the reality of the particles and qualities by direct demonstration.

What this means is that all the various proofs and tests of entanglement and superposition have been nothing more than strawman proofs and tests. The proofs and tests began by assuming that x would happen if entanglement were true, and that y would happen if hidden variables were true, then showed that x was true (or nearer true than y). However, the assumption that y would happen without entanglement was never proved, demonstrated, or even indicated. It was always only a pathetic straw men, propped up by fakers. In this whole circus, John Bell played the part of the ignorant dupe, perhaps on purpose. His agreement to these initial assumptions was a magnificent blunder, which cannot be accounted for in normal ways. In other words, he can't possibly have been stupid enough to mess up simple math in that way, so one must assume that he did it to throw the game to the other side.

The CHSH (Clauser, Horne, Shimony, Holt) tests are just slightly more complex photon routes than the routes looked at in my second paper on superposition. The early tests were one-channel tests, but the more complex two-channel test is diagrammed above. The math is done only on the “simultaneous detections” of any of the four sub-channels. In other words, any of the arrows going into CM may trigger a simultaneous detection.
We can have [A1, B1], [A1, B2], [A2, B1], [A2, B2].
We are then given the equation:
C = [A1, B1] - [A1, B2] + [A2, B1] + [A2, B2]
If C>2, we are supposed to have proof of entanglement and disproof of hidden variables. Could that be any sloppier or any more pushed? You should ask yourself, why not have two minus terms and two plus terms, and say that if C>0, we have entanglement?

That is the cheat right there.
The reason is that even this simple math is pushed in ham handed ways, in plain sight. To see how, we have to study the operation a bit closer. The “simultaneous detection” must have a built-in margin of error, since there is no such thing as simultaneous. That is assuming infinite precision, and there is no such thing as infinite precision, either in quantum mechanics or in normal mechanics. So the box CM has to be tuned to allow some tiny Δt to be defined as simultaneous, and the Δt just above that as not simultaneous. We aren't told what that tuning is. Regardless, this skews the entire experiment, and I don't know who thought this was the best way to test anything. Actually, it is the worst of all possible ways to test this or any other theory. There are a nearly infinite number of ways to test entanglement without requiring “simultaneous detections,” so it must be assumed that this way was chosen because the physicists knew it was the best way to fudge the results.

You see, because Δt is not instantaneous, it means that all four “simultaneous” detections are guaranteed to be overcounted. The operation guarantees that each of the four coincidences is greater than 1. So if you have three plus terms and one minus term, you are guaranteed to find a result over 2. Just think about it. If the margin of error is .01, say, then you have:
C = 1.01 + 1.01 + 1.01 – 1.01 = 2.02
Proof of entanglement, right? No, proof of equation finessing!

It takes about ten minutes to figure this one out, and one does not even have to give the photons spins and put them through the device. The cheat is clear just from looking at the math. They claim that their experiments are getting more precise and sophisticated, but the only thing getting more sophisticated is the misdirection. They give their experiments more and more channels and more and more sophisticated polarizers, and more and more complex particles (like Josephson phase qubits), but this is all just to get your attention off that bold cheat in the math. Like a shell game player, they have to keep your eyes off the ball.

The detection loophole and other loopholes also act as misdirection, since they get you looking in the wrong place for errors. In law, this is called leading the witness. In politics, it is called playing both sides. The mainstream people who sell these Bell tests have tried to create a path for doubters, even telling you where and how you might doubt. They say something like, “We admit that doubt can creep in at point A and B, and we can understand our opposition looking closely there.” They then assure you that they have done everything possible to answer your doubts. But since there was never any real problem at point A or point B, you have been misled. Since the problem is at point C, you will have missed it.

That was enough to destroy all the CHSH Bell tests, but MM also wants to draw your attention to another hamhanded cheat. They keep your eyes on what classical physics would predict here—the number 2— and of what quantum physics predicts here—the number 2√2 = 2.828. They normally hide the results of these tests from you, telling you only that entanglement has been strongly indicated. But if you look for numbers, you don't find them. Wikipedia, for instance, has blurbs on all the early CHSH experiments, but no numbers. Did they find 2.000001 or 2.8279999? Without serious digging, you won't discover it. The early tests actually found small deviations, on the order of 2.07. Stronger violations in the area of 2.25 have been found since then, but the experiments have to be made more complicated to get higher numbers. The simpler the experiment, the closer to 2 it gets.

But the point is, if you put all the Bell tests since 1972 in a pile, and average them, you get nothing even close to 2.83. Even with all the awful pushes we have seen, getting worse every year, the average is still very much closer to 2 than to 2.83. So you may ask yourself this: how can classical physics predict 2 and quantum physics predict 2.83, and a result of 2.07 is still read as vindication of quantum physics? According to my math, the result is 3% off the classical expectation and 27% off the quantum expectation. Also according to my math, 3 is smaller than 27. Even at 2.25, we are at 11% and 20%. Still not even close. The classical expectation is much better.

Therefore, we have no indication of entanglement at all, and never have. For these Bell tests to convince someone of entanglement, there would need to be two plus terms and two minus terms in the math. Then I would need a series of results that converged on the actual quantum prediction, with some logical margin of error. That would be real science.

Which leads to another question you can ask yourself: “What does it mean that we have had 40 years of media coverage trumpeting entanglement, 40 years of Bell tests claiming to disprove Bell's inequality, Bell himself caving, and no one arguing for sense in all that time?” How is it possible that such a bald mathematical cheat has been sitting in the open for 40 years, and no one has spotted it? Did Bell really fail to spot it? Is that believable?