The Mechanical Cause of the Golden Ratio
© Miles Mathis First posted January 11, 2011 As a place to begin, the problem is perhaps best put this way: "Why should the larger member seek a size or position that balances the smaller member and the sum? And how could the two members position or re-position themselves, once this balance was chosen?" In other words, we require a feedback mechanism. The two bodies that "seek" the golden ratio would require a form of communication. This has always seemed mysterious, since it is not clear that plants, celestial bodies, etc., could communicate in this way. But now that we have discovered the charge field, and shown that it is a real mechanical field already existing in the field equations of Newton and Einstein, we may look at this problem anew.
So we have at least two big questions to answer in this paper, questions never answered before:
What we will find is that the two questions have the same answer. The charge field is not just a medium that facilitates the golden ratio, by allowing for mechanical communication between bodies, and thereby a feedback mechanism. No, the charge field is what causes the bodies to tend to the golden ratio in the first place.
We can see this if we remember that all bodies are emitting a charge field, and that they are emitting based on their size. More rigorously, they are emitting based on their mass and their surface area. We need to know how many emitting particles there are in the body, and the mass tells us this. And we need to know how much space the body is emitting into, and the surface area tells us this. Let us take the Earth and Moon as our test or sample bodies, and let us imagine they are both perfectly spherical. We know that the Earth exists in the Moon's E/M field at all times, and we know that the Moon exists in the Earth's E/M field at all times. Given that, we may ask what this "existing in each other's charge field" might mean, mechanically and in the long term. No one has ever asked that, have they? Although we now know of the E/M field of celestial bodies (the magnetosphere as well as the electrical sphere), no one has spent much time theorizing about its long-term effects. Until recently, celestial mechanics has been dominated by the gravity field; and even now that plasma physics has gained some traction, it is admitted by only a few that E/M may play a sizeable part in the whole. But be that as it may, we may still ask how this "existing in each other's charge field" might play out. Whether or not you believe that celestial mechanics are governed solely by gravity, you can ask this question.
To answer it, we will work backwards from currently accepted numbers. MM has used this trick successfully many times in other problems, and it will be useful here again. If we use the two parameters above, mass and surface area, together we get a sort of spherical density. We get the amount of emitting matter we have in a spherical space. And if we look at the known densities of the Earth and Moon, we find the numbers 5.515 and 3.3464. The ratio there is 1.648, which an astute reader was kind enough to point out is very near the golden ratio. When writing the paper The Secrets of the E/M field are revealed at the Moon's surface, MM had ignored the similarity to the golden ratio until he could explain it mechanically.
In the above paper, we see that the Moon needs to increase its density to about 3.4 to reach the golden ratio. Two questions come to mind: is it doing that, and why would it be doing that? A third question is, how would it be doing that?
The third question is the easiest to answer. The Earth is being bombarded by charge from everything around it, and so is the Moon. So the Earth is being bombarded by (everything + Moon) and the Moon is being bombarded by (everything + Earth). Therefore, the Moon would be expected to be gaining density slightly faster than the Earth. MM does not mean that the Moon is gaining weight from photons or charge, but rather it is the bombardment that is actually squashing it a bit. The Moon feels more charge pressure than the Earth, and so it gains density faster than the Earth. It gains density because it is in the heavy charge field of the Earth.
You will say, "If that were so, we would have clear evidence of it. Since the Moon is always showing the same face to us, this 'squashing', as you put it, would happen mainly from one side." Amazingly, we do have that evidence. We know that the Moon is being squashed more in front, and we have known it for decades. Current schematics of the Moon clearly show a deformation or obliteration heaviest nearest the Earth. The nearside crust has been almost completely blasted away, with the heaviest blasting centered at the nearest point. The nearest part of the Moon IS being squashed the most, as we would expect given a charge field.
The first question is simply one of data, and it appears that the Moon is gaining density very slowly. It is doing this by getting smaller, just as you would expect from something that is getting squashed. If a body gets smaller and keeps the same mass, it gains density. My theory was bolstered just last year, when headlines all over the world announced that according to NASA, the Moon is getting smaller. Some will say that NASA did not mean to provide proof of MM's theory, and that we have no similar data showing that the mass has remained stable over the eons (which MM's theory would require). But the data from NASA is about as good as any data we are likely to get on this question, since we have not been monitoring the radius of the Moon long enough to compare it to the mass. Real proof of MM's theory from data would require monitoring both radius and mass over millions of years, and we can't have done that, obviously. But these indications of noticeable shrinkage are strong if incomplete evidence that the Moon is gaining density. So we have straightforward answers to questions 1 and 3.
Now for question 2. Why would the Moon be tending toward a density of 3.4? Again, working backwards theoretically, we propose that it would do so because it is in the charge field of the Earth. Because the Moon and Earth are very near, they exist within one another's charge fields. Of course, everything exists in the charge field of everything else, but, due to the nature of the field as emitted by spheres, it must tail off very quickly with distance. To feel the charge field as emitted by a sphere, you must be quite near it. This is another reason charge has been ignored in celestial mechanics: in many instances, it really can be ignored. The direct charge effect of the Sun upon the Earth is small, for example, due to the nature of the field. Even though the charge emitted by the Sun is stupendous, it has already mostly dissipated at the distance of the Earth (relative to the other strong forces at the Earth). We get huge charge side-effects here, due to the Solar Wind and so on, but this is due to the ions driven along by the photons. Without the ions, the photons spit out by the Sun would have a minimal field effect here, relative to gravity, the ambient charge field, the Solar Wind, and so on.
At any rate, although the charge field (of specific bodies) is a small player at great distances, at smaller distances like between the Earth and Moon, it can be a big player. And in the presence of ions, it is a very big player. We know there are lots of ions between here and the Moon, so we have a mechanism available. We have a mechanism, but we don't have a cause. We could explain an effect, but we don't yet have a viable theory for an effect, do we?
To define the Moon example in the words of the golden ratio explained mechanically in the earlier part of this paper; the Moon is affected by (everything + Earth) and the Earth was affected by (everything + Moon). Before we unlock the secret, let us study those words a bit more closely. One might say that one could apply that sort of word-math to any two bodies at random, but that isn't really true. MM has shown, the Earth and Moon are affecting one another via the charge field in a way that nothing else is affecting them. They are feeling weak charge from all other nearby bodies, but strong charge from one another, due only to distance. Also notice that they are feeling the same overall field from outside. In other words, the Moon receives the same forces from all other bodies that the Earth does. In this way, the “everything” of the Moon is equal to the “everything” of the Earth. Whatever the Earth receives from the Sun, the Moon also receives. Whatever the Earth receives from Jupiter, the Moon also receives. Whatever the Earth receives from the galactic core, the Moon also receives. This is simply because the Moon is orbiting the Earth. The center of the Moon's space is the also the center of the Earth's space. The distance of the Earth from the Sun is 1AU; the distance of the Moon from the Sun is 1AU. Etc.
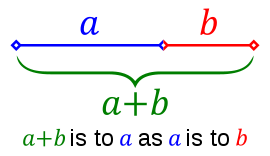
We can turn this "everything" upside down and put it into the golden ratio, like this: the golden ratio can be stated “small is to large as large is to sum.” But “everything” really means "everything except the sum." When MM says "everything" above, he means everything outside the Earth-Moon system. The Earth-Moon system is the sum, therefore "everything" means "everything except the sum." To put it another way, we now have four variables or entities to work with where we had three before. In the golden ratio, we have a, b, and (a+b). This way of writing the math makes us think we only have two or possibly three players, so we cannot understand how the three terms influence one another. But MM has just shown that we really have a, b, (a+b), and (everything beyond a+b). Up to now, we have represented the golden ratio by line segments or triangles, but these representations are incomplete, because they leave out "everything else." Because we think "everything else" is stable or constant, we ignore it. We don't represent it in our drawings or math. But the physical fact is that "everything else" is influencing a and b all the time. Not only that, but “everything else” is related mathematically and mechanically to a, b, and (a+b) all the time. This will give us both the math and cause of the math.
To make this a bit less airy and philosophical sounding, let us re-assign variables. Let us change the name of (a+b) to c, and (everything beyond a+b) will be d. The universe is now represented by c+d, which we will also give a variable, u. Now, instead of just looking at how a and b relate to one another, we can look at how a and b relate to u. This is how the universe and how physics really work. Perhaps now you see that the current math of the golden ratio treats a and b as straight co-dependents or functions, when they aren't. The golden ratio couldn't be understood mechanically as long as we were trying to define a and b in terms of one another. They aren't physically defined in terms of one another only. The terms a, b, and a+b are all functions of d and u.
Let me state that one more way, for good measure. If we treat a+b as a line segment, we must remember that a line segment is defined as a partial thing. A line segment is part of a greater line. If you have the segment that is between a and b, you also have the segments that are not between a and b. The current representation ignores that. If you represent phi by a triangle, you not only have what is inside the triangle, you have what is outside the triangle. The current representation ignores that.
This may sound like Zen or yoga to many people at first, but it is straight math and physics. Physics is always applied math, and if you have faulty or incomplete variable assignments, you have faulty or incomplete math. The historical representation of phi has been at least one variable short.
A reader will say, "What do you mean, a variable short? We can't assign a variable to infinity, can we? If you include the “line segments” on either side of (a+b), you only have two infinities!"
MM is not being esoteric here, but will remain mechanical. It is current mathematicians and physicists who are airy, not MM. They are the ones that teach that math is or should be pure. They are the ones that tell you not think of math in terms of tangibles. They are the ones that tell you to learn calculus without asking for visualizations. They are the ones that tell you not to expect quantum mechanics or relativity to make sense. They are the ones that tell you to shut up and calculate. If you can't understand the physics, they tell you to stick to the math. MM is doing the opposite. If you don't understand the math, go back to the physics. Go back to something tangible or physical. If the math hits you with an infinity here, go back to the physics. It will show you how to get around the infinity.
Go back to the Moon+Earth problem. We want to represent the "everything" beyond the E+M system. Although space may or may not be infinite, we don't need to represent "everything" by an infinity. We can more easily represent it by 1. We let the universe be 1 or totality, in which case the E+M system becomes 1 – d. The Earth is then 1 – d – b, and the Moon is 1 – d – a. We can then rewrite the golden ratio as
(1 – d – a)/(1 – d – b) = (1 – d – b)/( 1 – d)
You will say that is just juggling numbers, but it isn't, because the question has changed. We aren't asking why the smaller body should be in the same ratio to the large body as the large is to the sum, which is the same as asking how the two relate to one another. No, we are asking why the two variables a and b relate to the number 1 in such a way as to create this equality. The two variables are functions not only of one another, but of the number 1. The way the current equation is written, this cannot be seen, because even if we try to think of the problem in this new way, we end up trying to write the two variables as functions of each other and infinity, which is impossible. This way, we see how the number one can limit the math.
This new representation solves the problem not only mathematically, but conceptually. Although the universe may or may not be infinite, we know the unified field force from the universe upon the Earth and Moon is not infinite. It is some real and therefore finite force. This being so, the forces of the Earth and Moon upon one another must be some real fraction of this total force. So a, b, and d can all be written as fractions, or as parts of the number 1. This automatically makes them functions of the number 1, and allows us to limit the math. The variables a and b are not just functions of one another, they are functions of one another and the number 1. Or, to say it another way, the Moon and Earth are not just functions of one another, they are functions of one another and of the total unified field at the Earth. The total unified field at the Earth/Moon acts as a sort of wall against which a and b can bounce. The values of a and b are limited not only by a and b, they are limited by the total external field.
Some readers will balk here and tell me that the charge field, or whatever MM is using as this limiting wall, is not big enough to act as a wall. They will say we have no evidence of such an "ether," and so on. But of course we do. We have centuries of evidence, if not of an ether, then of an electromagnetic space that surrounds everything. Mainstream physics has just ignored it for the last century, because it conflicts with their current equations. They don't want to rewrite all their Nobel-Prize-winning math, so they ignore mountains of old evidence, and new evidence coming in every day (see MM's other papers to find these many mountains). In the paper G is the Key to the Secret of Gravity MM has shown that the charge field exists prominently in the field equations of Einstein and Newton, and has all along. Not only that, but in the paper The Galactic Rotation Problem, he has shown that this charge field is what physicists are now calling dark matter. Dark matter is not non-baryonic, it is photonic. The only thing these physicists have right is the percentage of "dark matter." They tell us that 95% of the universe is dark matter. No, 95% of the universe is charge photons. Charge outweighs everything else by 19 to 1. Which makes it perfectly capable of acting as a wall in this current problem.
Other readers will still not understand how this provides a mechanical or mathematical solution. They will say, "Fine, you showed some mystical influence from the rest of the universe. But the question remains, why the number 1.618 instead of some other number? Why does the smaller body tend to be the same fraction of the large body as the large body is to the sum?"
The answer to those who keep asking this is, "You are still seeing the problem upside down. You are seeing a and b as functions of one another only. They aren't. The smaller body doesn't tend toward that fraction of the large body. Both the large body and the small body simultaneously maintain a relationship with one another and with the universe." The Earth is being pushed by both the universe and the Moon, and the Moon is being pushed by both the universe and the Earth. It is these combined influences that create phi. The current equation is incomplete because it tries to represent the problem as a pure math problem. As a pure math problem, the line beyond ab can be ignored. But the problem of the golden ratio is a physics problem, not a pure math problem. Pure numbers don't tend toward the golden ratio. Numbers applied to real things tend to the golden ratio. Therefore we have to study the mechanics of real bodies to understand the golden ratio.
Mathematicians have long known that it requires constraints to create the golden ratio. The golden ratio is a sort of feedback mechanism between two variables, forcing them into the ratio. They can show these constraints mathematically, but they cannot show them physically. Put simply, the golden ratio is the only solution to x – 1 = 1/x. Mathematicians can show you tricks with that all day long, but they can't tell you why phi shows up in nature, although we know that it does. That is what MM is doing here. The short answer is that pure math doesn't have the complexity necessary to solve this. That last equation has only one variable in it. The more popular form of the golden ration has two. But that still isn't enough. We have to give the constraints variables, also, in order to show the mechanical cause of the ratio. And once we have given the constraints variables, we have to assign those variables to something. That is the other historical problem here: without the charge field, physicists had nothing to assign the constraints to. Gravity is completely incapable of causing the golden ratio, and most physicists in history came to see that pretty quickly. So they gave up. That is why the problem still exists today.
It may help to look more closely at the physics involved with the Earth/Moon problem. Again, if the math is unclear, look at the physics. This is just the opposite of the current mantra, which tells you to stick with the math when the physics gets hard. MM has shown above that the Earth and the Moon are in the same field, with regard to distance from other objects. Since the Moon orbits the Earth, it is the same average distance from the universe. But because the Earth and Moon are not the same size, they do not react the same to the same unified field or the same unified force. Because the Earth is larger, it encounters a larger section of the field; and because it is denser, its constituent particles get hit more often. Therefore, the Earth feels more force from the ambient field than the Moon does. This is how a and b are functions of 1, and how a and b are not the same function of 1. This is why the current math and representations don't work: they ignore the variable influence of 1 upon a and b. They ignore the line beyond the segment ab, which is a mathematical and physical mistake. The line segment beyond ab is not a constant and cannot be ignored. It is a variable, and must be included in the math.
This realization allows us to extend our equation above once more, to flesh it out. For we now see that we don't just have a, b, c, and d, we have a, b, c, d as felt by a, and d as felt by b. Or, to say it the long way, we have the Earth, the Moon, the Earth+Moon, the universe as felt by the Earth, and the universe as felt by the Moon. We have FIVE dependent variables. This is why the number five is important in problems concerning phi.
We can see this clearly if we look at the triangle visualization of phi. This is the figure they publish at Wikipedia and all the other physics pages:
Ignore all the blue tags and we will concentrate on the line segments, whose lengths represent the forces of our bodies upon one another. This visualization is useful because it allows us to represent and tag our five variables. Like this:
[As you see, the tags of Wikipedia have been ignores and re-assigned to MM's own variables to the golden triangle.] To say it in English, the line segment CA is the force of the rest of the universe upon the Earth, and CB is the force of the rest of the universe upon the Moon. We see that they are different lengths, and MM has shown that this is because the Moon and Earth are different sizes. We also see that the angle at C is bisected. Until now, this was just a fact, unexplained. Why is the angle at C bisected? And why is C where it is, and not at some other point? For example, if C were moveable, we could slide it over until it was equidistant from A and B. In that case, we could slide X to the midpoint of AB, and the angle at C would be bisected. Why does C want to be bisected where it is in the figure, and at no other place? In other words, why does CB want to be the same as AX? In English, why does the force of the universe upon the Moon want to be equal to the force of the Earth upon the Moon? As you can see from the figure, CB = AX. Why? Simple. If the forces weren't equal, the Moon wouldn't be in equilibrium. It wouldn't stay were it is. The Moon keeps its position in the universe because the forces from the Earth and the rest of the universe balance at the Moon.
So we have found that the force from the rest of the universe upon the Moon is not only finite, it is relatively small. It is the same as the force from the Earth.
You will say, "But isn't the charge force from the Earth a vector? At any one moment, the Earth is only one direction from the Moon, so the charge force from the Earth to the Moon must be directionalized, or uni-directional. The force from the universe is not uni-directional; it is coming from all directions. How can these forces balance?"
That's a good question, but it is easily answered. The best way to answer it is to think of the old "equal and opposite rule" of Newton. And, again, to think of the ambient charge field as a wall. MM has shown that the ambient charge field is 19 times more massive than matter itself, even in the vicinity of matter. Since the Earth and Moon are creating their charge fields by recycling this ambient field, their emitted fields cannot be stronger than the ambient field. Their emitted fields must be weaker, especially at any distance from their surfaces. Therefore, the charge fields of these bodies, although perfectly capable of transmitting large forces, are not capable of trumping the ambient charge field. Think of it like this: you are quite strong and are capable of transmitting forces to anything you touch. But the wall in your room outweighs you by many times. If you push on it as hard as you can, you cannot move it. But that does not mean that you have not transmitted a force. You have. You have applied the force and the wall has matched it exactly, in reverse. So you have large forces with no movement. That is what we have here with the Moon. The Earth has applied a large force, and the Moon, held by the ambient charge field, has matched it. Forces without motion.
You will say, "Good grief, if the charge field is that strong, how does the Moon ever move in its orbit?" Well, MM never said the charge field was that strong. MM said the ambient charge field was stronger than the Earth's charge field at the distance of the Moon, that's all. But relative to the forces that cause the Moon to orbit, the ambient charge field is very small. The ambient charge field is 19 times more massive than normal matter, but by normal matter MM means things like protons, not things like satellites. The ambient charge field can resist a weaker charge field, but it cannot resist (much) the Moon travelling at over 1km/s. Besides, if you are asking this, you need to remind yourself that MM is explaining a golden ratio in the density of the Moon, not in its position. If you want to read about the orbital motion of the Moon in the unified field, you need to go to one of MM's other papers.
"OK," you will say, "But we are drifting into mud here. You still haven't explained why the Moon and Earth are in a golden ratio. The Earth and Moon could be any size at all relative to one another, and all you have said would still be true. If the Moon and Earth were the same size, the charge field from the universe would still match the charge field from Earth to Moon and maintain equilibrium, according to your mechanics. CB would equal AX, but nothing would be in golden ratio. It is not enough that CB = AX. You haven't shown why the angle is bisected for one thing."
Well, we aren't in mud, we are just answering questions that must be answered. But yes, we do still have some loose strings to tie up. To do this, we go back to the golden triangle. To achieve the golden triangle, not only must CB=AX, but the angle at C must be bisected. Only when both these requirements are fulfilled do we achieve the golden triangle. If CB=AX and the angle at C is bisected, then we must have a golden triangle. Those are the pure math constraints, and they have long been known.
Before we move on to the equal angles, we must finish explaining the importance of CB=AX. This entire paper hinges on understanding that constraint, and that equality. If the Moon and Earth were the same size, as a critic says, then CB could not equal AX. Consult the triangle again. If AX=XB, and if C is not on the line AB, then CB cannot equal AX. This is not to say that equal partners are disallowed in close systems like this, it is just to say that there is a constraint. The ambient field "likes" for CB to equal AX, because then the system is in a lowest energy state: the ambient field is resisting AX as little as possible, you see. The ambient field cannot resist AX with a lesser force, since the ambient field is fundamentally greater. The ambient field can resist AX with a greater force, but it doesn't like to, since that is not efficient. So the two forces tend to balance, naturally creating the golden ratio. Think of you pushing against a wall. The wall, being larger, could resist you with an equal force or a greater force, but it couldn't resist you with a lesser force. Simply because it is larger, it must resist with a force at least equal to yours. But it would be inefficient for the wall to resist you with a greater force: it would have to create internal pressure to do so. So the wall "prefers" to match your force exactly, in any situation it can. Likewise with the charge field resisting a force on the Moon by the Earth. The field, being the largest force present, can answer the Earth's force with a greater or equal force. If the Earth and Moon were the same size, the field would have to answer with a greater force, as we see from the triangle. But, given the choice, the field will prefer to answer the force with an equal force. Since the system of the Earth/Moon has give (like all systems), the charge field will push the system to the lowest energy state. The charge field will prefer to be lazy. If the Moon is anywhere near the golden ratio, the charge field will try to push it to that lowest energy state. Since the Moon has give in its density (is compressible), the charge field works preferentially on that parameter in this case.
So MM has shown why CB=AX, but not why the angle is bisected. As a useful visualization, you may think of the angle as representing the way the force from the universe arrives, and the line segments CA and CB as how the force from the universe is felt. MM has already shown above that the Moon and Earth are the same distance from the universe. The force therefore arrives equally to both Moon and Earth. But MM has also shown that the force is felt unequally, since the Moon and Earth are different sizes. So the two angles at C are equal because the field itself is equal to itself. The field at the Earth is the same as the field at the Moon. The angles represent the field itself. But the unequal segments CA and CB represent how the Moon and Earth experience the same force. From the point of view of the universe, the forces applied are equal. From the point of view of the bodies, the forces are not equal. Our math and diagram must represent this fact, and the way they represent it is by making the angles equal and the segments unequal, you see. The only way to make the angles equal, the segments unequal, and CB=AX, is with the golden triangle. In this way, the number 1.618 is forced to appear by the requirements of the field.
MM does not need to prove these mathematical requirements, since they are already known. It has already been proved by others before me that these requirements necessarily produce the golden triangle. Rigorously, it was proved in the other direction, meaning that it was proved that the golden triangle necessarily produced the bisection and the equality CB=AX. But, as MM has shown, in physics it is the reverse that is true. It is the field that causes the triangle, not the triangle that causes the field. We are not given a golden ratio, achieving the bisected angle. We are given the bisected angle, and we show that it must build a golden triangle.
My tough reader will say, "Fine, but all that would still apply if the Earth and Moon were equal. Are you saying that the charge field would push a Moon as big as the Earth down to its present size?" No, that is not what MM is saying is that there exists a mechanism in the charge field to push bodies that are near the ratio into the ratio, over long periods of time. MM is saying that the charge field provides a constraint, and that this constraint tends to push bodies into certain ratios, one of them being the golden ratio. In future papers, MM will show how other ratios may be "privileged" by the charge field. In two body systems, this would include the ratio phi/2 and so on. With multi-body systems, the ratios would be more complex.
One of the many reasons this was not seen before is that the golden triangle has been mislabeled and misanalyzed. You can see this from Wikipedia's labels, where CB is labelled as phi. That is not wrong, but it is mechanically useless. What MM has done is let AB stand for our original line segment ab, then take C as a point off the segment that can influence the segment. In this way, we create the same golden triangle, but the point C is now assignable to a real field. In the Wiki diagram, C is not assigned to anything. It is just a mysterious third point, floating in undefined space. In MM's diagram, C becomes a representation of the field at ab, and this allows us to solve the problem mechanically.
To say it another way, MM started off (way above) by proposing that the line beyond ab should be included in the analysis of ab. MM stated that the line beyond ab should be capable of influencing ab, since this problem was physics, not pure math. But in that case, everything was linear. All we had was a number line. It was not especially clear how the line beyond ab could affect ab, even after MM showed that it could be represented by 1 rather than infinity. To make this more clear, MM brought in the third dimension. A line has two dimensions, but a triangle has three dimensions. Rather than influence the segment ab from along the original line, MM moved the influence off the line, and influenced ab from a point C. This created a triangle. Although this clarified the mechanics a bit, it still created a compression of reality, since the universe is not really affecting ab, the Earth/Moon, or anything else from a point. In reality, the universe is affecting ab from all points. But that would be impossible to represent in a diagram, for obvious reasons. So we compress the variables, letting some be represented by angles and others by lines, in order to draw them.
Please note that this paper is a simplification by me of a paper or papers written and copyrighted by Miles Mathis on his site. I have replaced "I" and "my" with "MM" to show that he is talking. All links within the papers, not yet simplified, are linked directly to the Miles Mathis site and will appear in another tab. (It will be clear which of these are Miles Mathis originals because they will be still contain "I" and "my".) The original papers on his site are the ultimate and correct source. All contributions to his papers and ordering of his books should be made on his site.
(This paper incorporates Miles Mathis' phi paper and phi2 paper.)
Abstract: Miles Mathis will show the mechanical cause of the golden ratio in physical problems. MM will do this by expanding the variables in the math to include the ambient field. MM will show that this field, which is the charge field or the unified field, is both the cause and the medium of the golden ratio in physical problems. It is the physical constraint that pushes the numbers into golden ratio.
1)Why would inanimate objects, of any size or relationship, desire to be in a golden ratio? Or, put less provocatively, why should they tend to that ratio, mechanically?
2)How does the charge field act as a medium, either facilitating or actually causing the bodies to move to the golden ratio?
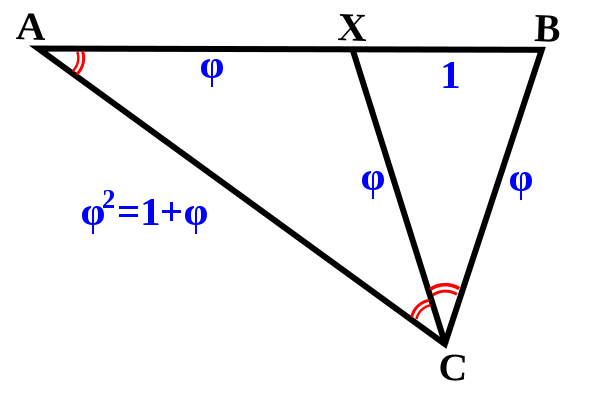
a = AX
b = BX
a+b = AB
da = CA
db = CB

If you are still having trouble, study the triangle as it is created from the point of view of point C. Put your eyeball at C, and pretend you are the universe affecting some given system. Let AX be the Earth and XB be the Moon. From point C, the field is emitted the same to both bodies. That is what the equal angles represent. The field as emitted from point C is the same for the Earth and Moon. Because the Earth and Moon are equal distances from C, the total field, we let the field split into two equal parts, hence the equal angles. But then we have to represent the unequal sizes of the Earth and Moon relative to the field. We do this by drawing AB at a slant to C. So although the field left C in equal parts, it arrives at AB in unequal parts. Do you see it now?
We may now return to our original statement of the golden ratio, for more analysis. MM began this paper by stating the golden ratio in one of its commoner ways: small is to large as large is to sum. But since MM has shown that CB = AX, and since AX is "large," we may make a substitution. CB is the force of the universal field upon the Moon, the Moon being "small." So the statement of the golden rule becomes "small is to the force upon it as the force upon it is to the sum." Or, a variation: "the force of the Moon upon the Earth is to the force of universe upon the Moon, as the force of the universe upon the Moon is to the combined force of Moon and Earth." Using my variables above, this would be
a = db
b/db = db/(a+b)
Then we go back to the other expression of the equality:
1/φ = φ – 1
b/a = (a/b) – b/b
b/db = (db – b)/b
combining the two, we get
(db – b) /b = a/(db+ b)
ab = (db – b)(db+ b)
This is a useful equation, because if you can visual that equation, you can visualize why the Moon is pushed toward a golden ratio by the ambient charge field. The product ab is the Earth/Moon system, or the total force between Earth and Moon. The variable db is the ambient force upon the Moon, and b is the force of the Moon back upon the field. So you can see how the ambient field acts as the constraint that pushes the other variables into golden ratio.
Finally, MM will be asked why the golden ratio shows itself in the density and not in some other parameter, like mass, radius, or orbit. This itself is proof of the theory, because density is the logical place for the unified field to show itself. MM has shown that the constraint that causes the golden ratio is provided by the unified field, especially by the charge part of the unified field. Well, as those know who have read MM's other unified field papers, density is the most important unified field number for any body. It is the most important because it contains both fields, and expresses both fields. To calculate in the unified field, mass isn't enough. You need to know how much mass in how much space. MM showed this most clearly when he exploded Newton's gravity equation. Newton's gravity equation actually contains both density and volume, since mass can be written that way. However, his equation, without MM's expansion on his site on weight, has no way to plug in all the variables. You can only put masses into his equation, and that isn't enough information for the equation. The equation, to work properly, needs to know how much mass in how much space. That is a matter of density. Density is the primary variable in the unified field, so we should not be surprised to find that when the unified field is providing a mathematical constraint, we find it is constraining density. That would be the first place to look.
Of course there is much more to be said on this problem, but it should be clear that phi in nature is not a coincidence. There are numerical coincidences in Nature to be sure, but most of the number relations that have been passed off as coincidence or numerology are probably just mechanical phenomena yet to be explained.
More on the Golden Ratio and the Fibonacci series
Previously here, MM showed how the unified field causes a field constraint that could lead to the golden ratio in natural situations; now here he will have something important to add to that.
That paper was somewhat complex as a matter of influences and kinematics, but this one will be much simpler. MM was looking at a simplified expression of the golden ratio today, one MM wrote himself instead of getting it from the textbooks, and it led me in a somewhat different direction. The golden ratio is commonly written in terms of φ, which has the value 1.618. But it can also be written in terms of what is called the conjugate Φ, which has the value of .618.
Historically, that was the initial esoteric thing about the golden ratio: it was the number that had an inverse that was equal to 1 + itself.
1/.618 = 1.618
It was that curious equality that initially intrigued mathematicians, not any infinite surds or Fibonacci series or anything else. Phi is normally written in equation form as
1/φ = φ – 1
But if we write it in terms of the conjugate—as we should—it is
1/Φ = Φ + 1
As you see, that is the more natural way to write the first number equation above. If we then multiply
both sides by Φ, it becomes
Φ2 + Φ = 1
We do that not because we are really interested in the number Φ2 = .382, but simply to get rid of the
ratio, allowing us to look at it more like a power series—or simply a power equation.
Now, the series form of the golden ratio—which leads to the Fibonacci series—is still interesting, and I am not here to overturn it or argue it down (it will be confirmed below). But this simpler form may tell us something as well. MM showed previously in this paper how we can look at the golden ratio as a field equation instead of a series, and we can look at this simpler expression as a field equation, too. If we let the number 1 represent “the whole field,” then we see that the other side of the equation is giving us just two terms, not an infinite number of terms. This expression appears to be telling us that the whole field is made up of some subfield, and also of a second subfield that is the square of the first. This may be of interest to us, since it is what MM found of his unified field. When the gravity field is changing by the square, the charge field is changing by the quad. Which means the charge field is the square of the gravity field, as a matter of change .
MM has not found that the energy of either field is the square of the other, notice. The charge force on a particle isn't the square or square-root of the gravity force. The square only applies to the field changes . Gravity falls off by the inverse square while charge is falling off by the inverse quad. Does this fact have anything to do with the golden ratio?
We are seeing that it does, which makes it curious that the golden ratio has never been connected to the inverse square law of physics. Even though no one before me had the two subfields as we do in my unified field, it seems someone should have noticed that the golden ratio concerns squares and square- roots. It would have been pretty easy to connect phi to the inverse square law, since phi and gravity both fall-off by the square. And even without gravity, phi should have been tied to the sphere. Why? Because the surface area of the sphere also falls off by the square. Any real field emitted by a sphere would fall off by the square. That would include gravity or anything else.
SA = 4πr2
Now, it may be that others have made this connection, but it isn't reported in the mainstream literature. It isn't at Wikipedia, for instance, and it seems a thing worth reporting, if you have it in your briefcase.
MM assumes it is not reported because no one has figured out how either the sphere or gravity can be the cause of the Fibonacci series in nature. The confirmed instances we see in nature don't seem to be the result of gravity or of spherical emission. For instance, although plants are in a gravity field, obviously, and this field is spherical, the field seems too big to explain the small changes we see. The gravity field of the Earth is very big, in other words, and curves very little. But the tendril is very small, and curves a lot. So the connection is not made.
However, MM's unified field gives us answers to both problems, and allows us to make the connection logically. It isn't the gravity field that is influencing the tendril, it is the charge field inside the gravity field. Since the charge field changes to the square of the gravity field, it changes very much faster. like tendrils. The charge field is also a field of particles (photons), which allows us to track the real influence in the field. We already know that plants respond both to the light field and to the E/M field, so the mechanism is no longer mysterious.
In the same way, the spherical nature of the field is explained. It isn't the large sphere of the Earth that is emitting here, forcing us to follow the small local curvature of that field. It is the nucleus and the proton itself that is emitting the charge field, allowing us to explain Fibonacci curves down to the smallest sizes. The real curvature of the tendril is then explained by the diminishing influence of some local spherical charge field, probably one centered in the plant itself. Some local bundle of ions is creating a charge field, and we are seeing the natural fall-off with distance of that spherical bundle.
MM will be told that the connection wasn't made because the Fibonacci series doesn't fall off by the square.
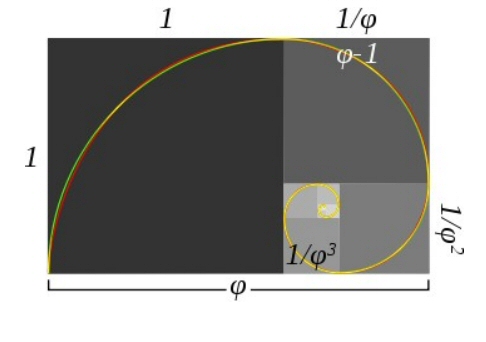
But it does if we analyze it correctly. MM can show you how to do that straight from this mainstream diagram. Start by ignoring the largest box. The box with a side of 1 won't help us study squares since 1 squared is 1. We will look only at the second box and the third. Now, ignore the boxes and look only
at the curves in those two boxes. You can see we have the quadrant of a circle in each. The length of the side of the box tells us the radius of the circle. The radius of the second box is r = 1/φ. The radius of the third box is r = 1/φ2 . MM would call that an inverse square relationship. If we then compare box four directly to box three, we get the same relationship, and so on.* If we look at each box as a field component (or fractal) instead of as part of a series, we do have an inverse square fall-off. In other words, the problem is they are writing and expressing the golden ratio as a series instead of a field. The Fibonacci series is actually the same as the unified field , and they both are based on the inverse square. Another way to say that is that they are writing the series as a series where each number is based on the first number in the series rather than as a series where each number is based on the previous number in the series. Notice that if you assign any box the length 1/φ, the box below it is its square.
If you still don't follow me, look here:
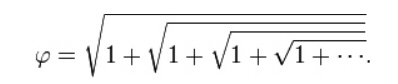
You can see phi falling off by the inverse square with your own eyes, by an equation called the infinite surd. That isn't MM's equation, that is Wikipedia's. That is written as a sum rather than as a series, allowing us to see the fall-off by inverse square. MM will be told that is falling off by the square-root, but the square-root is the inverse of the square. Some have said MM often seems to mistake the square-root for the inverse square. They aren't the same.
1/r2 ≠ √r That's true in a lot of situations. You can't just substitute one for the other in an equation. However, if you are doing relative field calculations—as MM often does—and you know you are in a field that varies by the square, you can use the square-root in your calculations. MM has done that often in his papers on Bode's law, axial tilt, and others. There, MM uses it as an inverse field manipulation, not as a substitution for 1/r2. We are seeing a similar thing here with the infinite surd equation, which—by the way it is written—stands as a diminishing square rather than as a series.
You should also notice something else about the infinite surd. The basic term is 1 + √1, which matches in field form our equation above Φ2 + Φ = 1 . In other words, what we see again is a field with two subfields, and one of the fields is the square root of the other. Because one field is inside the other field, we get this infinite regression when we write the field as a series. We are seeing clear evidence of the charge field inside the gravity field, creating the unified field.
How could so many people miss this? As usual, it is because they have too much math and too little mechanics. Instead of trying to visualize this as field mechanics, most people have been analyzing it as pure math. Most of the current and historical math not only doesn't help us see the field mechanics, it blocks it. And this example stands as a near-perfect indictment of modern physics, which has been hampered by a lack of visualization and physicality for at least two centuries. Since the Copenhagen Interpretation in the 1920's, it has been even worse, since visualization was no longer simply a rarity (due to the normal or average abilities of physicists); beginning with Bohr and Heisenberg, it was outlawed . Banned, verboten, förbjudet .
What this means is that the Fibonacci curve is just a sign of the charge field. The charge field falls off by the square inside the gravity field, creating this pattern of fall-off we see as the Fibonacci tendril. It curves rather than falling off in a line, because everything curves in the charge field. See MM's paper on the Coriolis effect , where MM explains that curve. The Fibonacci tendril can best be understood as a field combination of the Coriolis effect and the inverse square law, both of which MM has shown are caused by the charge field. The strength of the spherical charge field (which we call electrical when it moves ions) causes the fall-off, and the spin of the charge field (which we call magnetic) causes the curve.
If you don't understand what is meant by that last part, go back to the Fibonacci curve diagrammed above. Notice they turn the series 90 o by hand in between each box. Meaning, they just turn it because it fits the tendril that way, not for any mechanical reason that they explain. I f you ask them, “why are you turning the boxes each time?” They can only answer, “Because that gives us the pretty tendril.” But they don't use some sort of right-hand rule to justify it. They just do it. They can't use a right-hand there. But MM can. The curve actually is related to the right-hand rule, and this motion is related to the E/M field. Both are caused by the charge field, by the same fundamental mechanics. This section complements the earlier part of this paper, but is not a replacement for it. This section is a refinement and simplification of the fields described there, and should appeal to those who want just the barebones, with extreme clarity but very little exhaustiveness (or exhaustion). The earlier section was better at explaining how charge causes the (a + b)/a = a/b relationship and the parameters of celestial bodies like the Moon. This section is better at explaining the Fibonacci series.
*We know that box 4 is to 3 as 3 is to 2, so if there is an square relationship between 3 and 2, there is a square relationship between them all. The reason we don't find that square relationship between box 1 and 2 is that box 1 is arbitrarily assigned the number 1. But our series is not based on the number 1, it is based on the number . 618. That is why box 2 is our foundation, not box 1. This is also why we don't find a square relationship between box 4 and 3, with the given numbers. The given numbers are written as functions of 1, not of .618. In other words, if we divide 1/φ2 by 1/φ3 , we don't find a square. But again, that is because the series is not a function of 1/φ2 . It is a function of 1/φ. So the only relationship that will directly tell us that the series is based on the square law is the relationship between 3 and 2, as MM has shown.