Additive Color Theory and Antiphotons
© Miles Mathis
Miles Mathis finally returns to color theory after several years. You may remember that he wrote a colorful
paper on rainbows, then followed up with a long paper on Goethe and light theory. (Both papers are on his site).
(Excerpt from the latter paper rain2.html: "Let me summarize what we have found so far. We have seen that visible light is emitted at only two wavelengths. All visible light is originally red or violet . It can then become yellow or cyan when its spin speed is slowed by diffraction or refraction—by close contact with a charge field. Magenta and green are then created by a mixing of these four colors. This means that yellow and cyan wavelengths do exist, but they have to be created by charge interaction, since they can't be emitted.
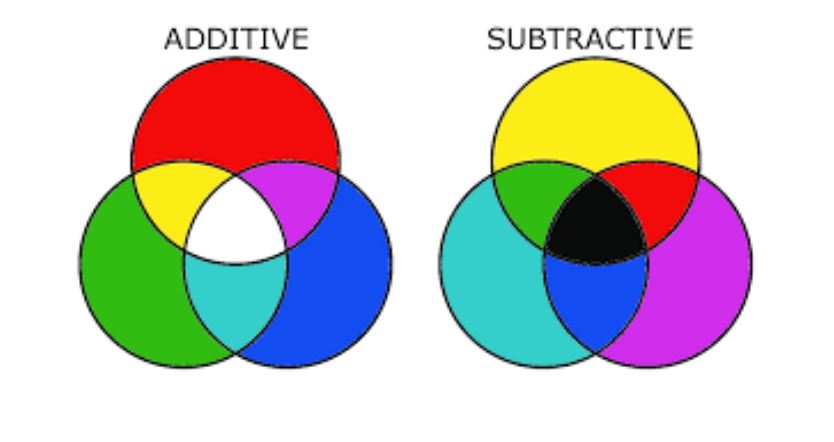
Additive color theory was one of the things MM only touched on before, and has come back to it
because it is so mysterious to him. Adding red and green to get yellow thumped MM's brain the first time he
saw it, and it is possible he has sat on it so long for that reason. Remember, MM is a painter, and if you
add red and green paint, you get a grey mess. In paint mixing, red and green are opposites, and it is
hard to intuit adding them and getting yellow. A painter can intuit adding blue and yellow to get green,
since even after you have the green, you can see the blue and yellow in the green. You can see and feel
how green contains them both. But if you mix red and green light, there is no way you can see red and
green in the yellow. Yellow is just yellow: it doesn't appear to contain either red or green. That is what
he means by intuit. It makes no sense.
Now, MM said in that previous paper that this works because green light already contains yellow and cyan
as it comes out of the projector. Red then knocks the cyan out, leaving yellow. But of course that isn't
the mainstream interpretation. While MM assumes subtractive color is primary, the mainstream has for a
long time assumed additive color is primary. They don't care about paint mixing because they aren't
artists. That means nothing to them. All they know is experiment, and they accept the additive color
mixing without really questioning it. There is no question of intuition here for them, or for asking if
anything makes sense. If red and green combine to make yellow, they do, that's all. Plus, there doesn't
seem to be any way for red to “knock the cyan out”, as MM claims, so they never even consider that
possibility. How and why could red be knocking cyan out of overlapping beams of light? There is no
easy answer to that, so why ask the question?
Well, MM has told you why he has asked the question, here and in the previous long paper. It is a
question to ask, because these experiments should make sense. We shouldn't just accept them without
trying to really understand them at the fundamental level. MM does not think many people besides him have
tried to do that. He didn't demand an answer from himself in that previous paper because he wasn't
prepared to give it at that time. MM had no answer or could intuit the raw answer, but couldn't justify
it with any convincing mechanics. Again, MM could see that the red must be “knocking the cyan out of
green”, but MM couldn't understand how it was actually doing that as a matter of field mechanics. Only
now can he begin to tell you that.
Remember, we aren't actually seeing the photons combine in the air to give us the colors. MM reminded you of that in the previous paper. What we are seeing is the colored light reflected off of a white wall.
This is very important, since white already contains all colors. Therefore, in both additive and
subtractive situtations, we have light bouncing off a surface: the two phenomena aren't that different.
In one, we have white light bouncing off colored objects, and in the other we have colored light
bouncing off a white object. It is not clear at a glance why they give us such different combinations.
Now, red light is also a mixture: a mixture of yellow and magenta. So it must be the magenta that is
opposite in phase somehow to the cyan. They cancel, leaving yellow. But cyan and magenta aren't
even color opposites: why would they be out of phase? What makes this doubly hard is that magenta
isn't even on the prismatic color spectrum, so if you look up a wavelength for it, you can't look on the
spectrum. If you insist on a wavelength, you find magenta is sold as a mix, being an average of red and
violet, at about 520. Since that is also the wavelength of green, we seem to have a major problem.
Green and magenta are opposites, but they have the same average wavelength?
The mainstream can't tell you what is going on here, but MM is going to “digress” to try to figure it out.
The mainstream tells us the brain simply makes up magenta as the opposite of green, to fill a slot. But
since that makes no sense, we have to search for a better explanation. Using MM's photon mechanics, we
can already see a way out of this mess. Although green and magenta do have the same average
wavelength, even in MM's theory, there must be more here than average wavelength. Green and magenta
must be opposite in some real mechanical sense. Since MM's theory contains both photons and
antiphotons, he suggests we use them here. Antiphotons are not mysterious in any sense: they are
simply photons spinning the opposite way. If photons in a field are spinning left, antiphotons are
spinning right. About 1/3rd of all photons on the Earth are antiphotons, and we have seen proof of that
in MM's other experiments and papers—including any paper that addresses positrons. Therefore, it
appears we need to rewrite all color theory and charts to include antiphotons. MM would say a good first
guess would be that while green and the other colors of the spectrum are photon colors, magenta is an
antiphoton color.
However, it appears it is even deeper than that. Notice that yellow and blue are opposites in additive
color, and so are red and cyan. But on the spectrum, cyan is above red, while yellow is below blue. So
we see the same weird dance there that we see with green and magenta. We seem to have a bending
one way with one pair and the opposite bending with the other pair. More on this below. Also worth
noticing is that red-green-blue are richer and more saturated to our eyes in the first instance than cyan-
magenta-yellow. MM has shown that this is because RGB are mixtures, but it may also be because RGB
are photonic while CMY are antiphotonic. Since the ambient field is twice as rich in photons to start
with, this may explain the basic saturation of RGB.
It would also explain the strange nature of magenta, which is the odd man out on both color wheels. Its
nature would be explained if its “average wavelength” was actually found in a different way than that
of green. In other words, green may be the average of photons and photons, while magenta is the
average of photons and antiphotons. You can't average photons and antiphotons in the same way,
obviously.
So let's return to the meeting of green and red to get some hints as to what is happening here. MM has
proposed that magenta and cyan are cancelling in some way, leaving yellow. But if magenta itself is a
mix of red and violet, we are in a vicious circle. Red cannot be composed of magenta, and then
magenta be composed of red. For this reason, one would say it is very doubtful magenta is composed of
red and violet. Because it has some similarities in our eyes to some shades of red-violet, it can be faked
in paint mixing that way. But it is likely that true magenta is its own color.
You can already see that including antiphotons in light theory complicates the mechanics considerably
—especially if antiphoton colors and photons colors are similar and overlap like this. For instance, if
some shades of yellow are photon and some antiphoton, we are in the middle of a real mess. MM would
say we are indeed in a mess, since it looks to me like almost all colors in nature are mixtures of photons
and antiphotons. If 1/3rd of all photons in the ambient field are antiphotons, then the light spectrum we
know and love must be composed of both. In that case, the lack of magenta on the spectrum would be
explained by the fact that the spectrum is a natural phenomenon. It is what we see in nature, in the
spectrum of stars, for instance. We don't see magenta there because in nature we never see antiphotonic
light only. It is always mixed with photonic light, and is always outnumbered by that photonic light
two to one. The only way we can see true magenta is to create it with specific set-ups, filtering it out of
mixed light. This is probably true of some shade of cyan and yellow as well, but since these shades of
yellow and cyan are very close to natural shades that are mixtures, we haven't yet figured that out.
After all, we only figured out the mystery of magenta recently. Neither Newton nor Goethe knew there
was any difference between magenta and red-violet, or that magenta “didn't have a wavelength”.
If that is true, what does it mean for us here? Well, it means that we have a pretty simple mechanism
for color cancellation. Notice that if magenta is the antiphotonic equivalent of the photonic cyan, the
two would cancel in some situations, leaving yellow. In other words, the photons of magenta are the
same size as cyan, but spinning opposite. This would create the equivalent of a wave cancellation, and
the loss of both colors. People will tell you that it is magenta and green that are supposed to have the same
wavelength, not magenta and cyan. However, there is some mystification online on this as well. Not
only do they generally refuse to tell you the energy or wavelength of magenta, they slide the 500nm
mark all over the place. It generally hits green, but here we see it marked below cyan.
Wiki gives the wavelength of cyan up to 520, which could match the energy of magenta. Wiki also
tells us complements of magenta have wavelengths of 500-530. So we appear to have a match.
But that was only to find the energies of magenta and cyan, since in MM's theory we won't be using
wavelength to explain anything. We are using opposing spins, and these spins are the real spins of the
photons. Yes, those spins create wavelengths, but since the wavelengths are one more step abstract, let's not to use them in the mechanical explanations.
So, how exactly does this cancelling of spins work? Well, all that would be required is some jostling of
photons as they travel side by side in the mix. Most photons don't affect eachother's spins much in that
situation, since the spins aren't greatly different. But when photons and antiphotons jostle like that,
they are strongly affected, since the spins are opposite. The spins catch like little gears and the outer
spins are tamped down. This is why and how magenta cancels cyan in this situation.
This tells us two things: 1) this is another analogue of magnetic reconnection, since MM has used the
same mechanics to explain that. We should call it photonic reconnection, or just photonic connection,
since it is actually a sub-magnetic effect. All magnetism is a spin effect, so it isn't wrong to call it
magnetic reconnection. But previously the name has led us to believe all such phenomena are EM or
ionic. They are not, they are photonic. 2) such magnetic reconnection must always be present, and is
only a matter of degree. Previously we have only studied it in extreme cases, as in the Solar corona.
But it now looks like this photonic connection is happening all the time in all places. In the current
effect, it is much more subtle, causing only color changes rather than spin ups or spin downs that lead
to extreme heating or lepton creation.
This also implies that any coherence that would minimize this jostling would also minimize this effect.
In other words, if we can force the photons to travel in perfectly straight lines to the target, they will not
jostle. If they don't jostle, they can't cancel spins. Of course, to do that, we would also have to create a
near perfect vacuum, including a charge vacuum. In normal situations, the ambient field is full of ions,
molecules and charge, which interact with the light, re-jostling it.
So, do we have any other indication MM's theory is correct? Yes. We discovered in MM's previous light
papers that when we look at this black print on a computer screen through a prism, the letters are split
into CMY. Here is what MM said there :
If you look at this black print through a prism, you fnd it turns magenta. Depending on the
orientation of the prism, you also get two ghosts. If the point of the prism is up, you get a
yellow ghost above and a cyan ghost below, with the yellow ghost higher than the cyan ghost is
low: the yellow ghost is about a full character above, while the cyan ghost is about a half
character below. If the point of the prism is down, you get a reversed effect.
That was always curious, though no one has commented on it until now. Even MM didn't see anything in
it the first time. Why would yellow be bent up and cyan be bent down? And why would yellow be
bent twice as much? The only possible answer is that the yellow photons are spinning opposite the
cyan photons. So one or the other must be antiphotonic. And we can tell that although yellow and
cyan are opposite here, they do not have the same spin radius or energy.
What can we tell about magenta from this experiment? We can tell it is opposite to either cyan or
yellow, and that it is equal in energy to neither. This would seem to contradict MM's previous theory,
since we need magenta and cyan to have equal energies in order to cancel. However, as with magenta
and red-violet, we may have more than one cyan to work with. The cyan here may not be the same
cyan we were looking at above. In other words, we may have a photonic cyan and an antiphotonic
cyan. Only one of those is opposite to magenta. If magenta is antiphotonic, it is opposite the photonic
cyan. That would mean we have the antiphotonic cyan being bent down by the prism, and the photonic
yellow being bent up.
It is also curious that magenta is not bent at all by the prism. This would seem to make it even more
special, though MM does not see how to read that right now. Much more work needs to be done in this line.
But if nothing else, MM believes we have strong proof of antiphotons here, as well as their inclusion in the
basic light spectrum. MM thinks you will agree this requires a complete rewrite of color theory.
One thing this tells us is that our eyes have a way to distinguish opposite spins. Since they can tell
magenta from green, they must be able to differentiate a spin from its opposite, or a waveform from its
opposite. If we speak in terms of waves, it appears that given waves of equal energy, amplitude, and
wavelength, our eyes can tell a left-wave from a right-wave. If they couldn't, we would see magenta as
green. It has always been assumed that our eyes register only wavelength, amplitude, or energy, but if
that were so we wouldn't see magenta. The brain doesn't make up magenta to fill a slot. That idea was
always daffy. The brain sees magenta just as much as it sees any other color, and it sees it by being
able to “see” spin differences in some way. So we are finding clear evidence that organic bodies know
the difference between photons and antiphotons. That should not be surprising, since although
antiphotons are not evil, they do work differently than photons. In some situations they may cause
cooling rather than heating, for instance, and the body would naturally be interested in that.
Please note that this paper is a simplification by me of a paper or papers written and copyrighted by Miles Mathis on his site. I have replaced "I" and "MM's" with "MM" to show that he is talking. All links within the papers, not yet simplified, are linked directly to the Miles Mathis site and will appear in another tab. (It will be clear which of these are Miles Mathis originals because they will be still contain "I" and "MM's".) The original papers on his site are the ultimate and correct source. All contributions to his papers and ordering of his books should be made on his site.
(This paper incorporates Miles Mathis' anticolor paper and an exerpt from rain2.html (a long paper on Goethe and light theory).)
By this analysis, red and violet photons are pure or fundamental photons (Due to photon spin), being emitted that way by matter. Yellow and cyan photons are secondary photons, since they are created by charge fields. Green and magenta photons do not exist, so these colors can be called optical tertiaries. Green is yellow plus cyan.")
Although that
second paper was quite comprehensive as well as revolutionary, of course it still only got us started on
a very big subject. Light theory is still in its infancy, and that paper only pushed it a baby-step forward.
Here MM hopes to push it another baby-step.