Planck's Constant and the Fine Structure Constant
| Please note that this paper is a simplification by me of a paper or papers written and copyrighted by Miles Mathis on his site. I have replaced "I" and "my" with "MM" to show that he is talking. All links within the papers, not yet simplified, are linked directly to the Miles Mathis site and will appear in another tab. (It will be clear which of these are Miles Mathis originals because they will be still contain "I" and "my".) The original papers on his site are the ultimate and correct source. All contributions to his papers and ordering of his books should be made on his site. (This paper incorporates Miles Mathis' planck paper,planck2 paper, fine paper, fine2 paper, fine3 paper, fine4 paper.) |


Planck Feynman
Abstract: It will be shown that Planck's constant is a paper wall built to hide the mass of the photon. After that in the last part of the paper the fine structure constant will be unwound to answer Feynman's question as to where the number comes from and why it is what it is.
Planck's Constant
It has now been 108 years (since 1900) that quantum mechanics has existed without a mechanical explanation of the quantum. That is to say, we have lived 108 years with a misnomer. Quantum mechanics is not and never has been mechanical. By the same token, Quantum Electrodynamics has never been dynamical. Both are theoretical and heuristic.
For quantum mechanics to be mechanical would require that we have a mechanical explanation of quantization, but we do not. We only have a mathematical explanation of quantization.
Max Planck—who discovered his own constant, of course—believed that the constant was only a useful device of problem solving. He did not believe in the actual quantization of energy. Or, to be more precise, he believed that quantization was an outcome only of absorption or emission: the energy could exist continuously, but only be emitted in steps. In a sense he was correct, as we will see. He was not altogether correct, in that there is a simple mechanical reason for quantization, and he never discovered or proposed that reason. To his credit, he resisted the Copenhagen Interpretation and all the fuzzy theory of “duality.” But because he could not show how the quantization was caused by emission, in a straightforward mechanical way, he lost the argument to the superior charm of Bohr and Heisenberg.
Bohr and Heisenberg defined the terms of quantum theory, and those terms still stand. Both Schrodinger and Einstein disagreed with these terms, but they have been outvoted. Today, top physicists either agree with Bohr and Heisenberg, or they don’t really care one way or the other. No prominent physicists now claim that quantum mechanics does or should have a mechanical basis. This mechanical foundation was ridiculed by Feynman, Pauli, Dirac, and is still ridiculed by Gell-Mann, Hawking, Weinberg, and the rest of the top names. For this reason, doubters have found it best to keep quiet.
As a matter of theory, we are stuck at the level of Bohr and Heisenberg. The foundations have not changed since the issuance of the Copenhagen Interpretation (CI). What the Copenhagen Interpretation said, in short, is that electro-magnetic radiation (usually including both photons and electrons) has a dual nature. It is both particle and wave. This much is true, and there is nothing against it. But what was novel about the CI is that its authors went much further: they claimed that this duality was inherently mysterious and could not be understood in classical or mechanical terms. Bohr and Heisenberg couldn’t discover a mechanical explanation (and neither could anyone else at the time) so, to save face, they decided that the problem was categorically insoluble. It was a problem beyond classical understanding, beyond the reach of visualization or illustration. But they went even further. They decided that this decision of theirs was final, and they all but forbade anyone from seeking for a solution after that. They could not pass a law, of course, so they did the next best thing. They created a cult. Anyone who continued to seek a mechanical explanation was ridiculed and ostracized.
You wouldn’t think such a plan could work in the “upper reaches” of science, but Bohr and Heisenberg and the rest (Pauli, Born, etc.) knew how to create fear. They went right at their biggest foe, and his defeat was the defeat of the entire opposition. Yes, this cabal defeated Einstein, and after that no one wanted to end up like Einstein. Each doubter looked at the facts and said to himself, “Well, if Einstein couldn’t win that argument, what chance have I? Best specialize in something else and keep my mouth shut.”
This has been the way of it for 70 years, at least. Not one big-name physicist has attempted to explain quantization or duality in a mechanical or classical fashion. A few, like Bohm and Bell, have made small steps in this direction, but they have never questioned the groundwork itself. That is, they have questioned specific points of the theory, but not the theory itself. They have not started over from the beginning and tried to build a logical visualization. Like the rest, they have accepted that this could not be done.
And so, in the year 2008, quantum theory, as a theory, stands almost precisely where it stood in 1927. We still believe in the dual nature of light, but we have no clearer picture of this duality than we had then. How could we? We were forbidden by the CI to seek a clearer picture, and physicists have stuck fiercely to their Constitution.
Physicists certainly would like a clearer picture of quanta and of light. That is one reason that string theory was invented in 1984. But they will not do the logical thing and seek to explain duality directly, by ignoring Bohr’s rules. They will not seek a mechanical explanation of duality.
Having given an explanation of superposition position in Superposition is not Mystical, entanglement in Entanglement: "Spooky action at a distance" is not real and suggested A Reworking of Quantum Chromodynamics and dismissal of the Quark, MM wanted to speak directly to Planck and quantization.That other papers are about stacked spins on the photon, and using them to explain the various detector mysteries and paradoxes, it did not explain fully the problem of duality itself. It is implicit, but it is best to be explicit with all rigor and emphasis.
The standard model states that matter has a dual nature, showing characteristics of a particle in some experiments and characteristics of a wave in others. But it does not tell us how matter expresses these characteristics. It assumes that it is impossible to do so. But it is not impossible. In fact, it is embarrassingly simple. Matter is NOT both particle and wave. Matter is a particle with a wave. That is, the photon, like the electron and the proton and every other incorporation of matter, is a discrete particle, with a radius, a surface area, a mass, and a spin. Fundamentally, it is not a wave. It is a physical sphere, just as much as the Earth or the Moon or a marble or a bowling ball.
So all those smug little PhDs on the forums are wrong. To solve the problem of duality, we must not think of the photon or electron as a probability. We must think of it as a physical sphere. We must do so because doing so is the only way to solve the mysteries of quantum mechanics. MM has already proved this in the most direct fashion possible: by solving problems that had stymied them for generations. MM has solved problems Bohr could not solve, that Einstein could not solve, that Feynman could not solve, and he has done it by ignoring all the warnings from the physics police who enforce the rules of CI.
They have said there is no way to visualize superposition, but MM has done it. They have said there is no way to illustrate wave motions or characteristics, but MM has done it. They have said there is no way to explain duality in a physical, mechanical way, but MM has done it.
|
MM has done it by showing that a simple sphere, of any size, can have four stacked spins.
This shows the exact mechanical cause both of the wave and of the duality. Stacked spins cause the wave. The particle is not a wave: the particle moves as a wave against a background, due to stacked spins. These spins may be caused simply by collisions. We may assume that particles collide all the time. If they survive collision, it is because the collision was indirect. An indirect collision would create a spin on any sphere of any size. Summed over a long period of time, these spins would tend to maximize in one direction or another. That is to say, simply as a statistical matter, we would expect all or most surviving particles to have all possible spins. This applies to photons and electrons as well as to free protons. |
It turns out that Planck was right: no energy state is outlawed by quantum theory. A particle or system can have any possible energy value, over a continuum. But given a specific interaction, like an emission or absorption or an orbit, a particle or system must change in a quantized way. This is due to the stacked spins. It is due to the fact that each spin is an integer value of the radius of the particle itself. Not just an integer, but an even integer! Yes, we may have the number three in the wave equations, but at the foundational level, we don’t have any odd numbers. In this sense, not only is energy quantized, it is an exponent of 2. At the very lowest level of energy measurement, the wave cannot have an odd value (relative to the radius, that is).
This is the root cause of quantization and of Planck’s constant. Planck’s equation is E = hν. Energy is quantized because frequency is quantized. Well, frequency is quantized because wavelength is quantized. Frequency and wavelength are straight functions of one another. The spin causes the wavelength directly. The electrical wavelength is 8 times the radius of the spinning particle. If the radius is 1, the electrical wavelength is 8.
Quantization is caused by simple rules of spin. Actually, just one rule: the rule of gyroscopic exclusion. You can’t have more than one spin about a given center. And this rule is not a bald postulate either. It is a logical outcome of motion and matter. That is to say, there is nothing mysterious about gyroscopic exclusion. To propose that two spins could happen simultaneously about the same center, you would have to propose that matter had no structure, at any level. To propose spinning the Earth around two separate axes that went through its center, you would have to propose that the Earth is structure-less sort of gas, with no interaction between particles. Likewise with any quantum. To apply gyroscopic exclusion to quanta we only have to assume that they are material, and that they are not points or point-like. This is the logical mechanical assumption that does not need defending. It is current theory that is illogical, in proposing that “matter” that expresses “energy” and causes real “motions” can fail to have “extension”. MM simply returns to classical assumptions, based on the definitions of all these words, in which matter must have extension. A point is a nothing, and you cannot propose that a nothing expresses energy, transmits force, or takes part in events.
The other problem this solves, of course, is the assignment of Schrodinger's waves. In the wave equations, we have four parameters that define every electron energy state. These four parameters are the four stacked spins, and my visualization is the first to explain the precise mechanical relationships of these spins. Of the four basic quantum numbers, one is already called angular, which is of course tied to spin. One is called spin. And one is called magnetic. This mirrors my assignments, except that my theory is strictly mechanical, assigning all four quantum numbers to real spins. One spin does indeed cause the magnetic field, but it is still a spin quantum number. All the numbers are spin numbers, as a matter of mechanics. Magnetism is not a quantum or mechanical quality. Magnetism is an outcome of the spin. Spin is the cause and magnetism is the field it causes, by bombardment and direct contact. Putting a mechanics under the wave equations also explains the Pauli exclusion principle in a direct fashion. We no longer need to rely on a mathematical interpretation, since we can see the physical reason. The reason is that electrons are actually positively charged. Meaning, according to my theory, that they are emitting a real field just like the proton. Although this field is both real and repulsive, it does not act like the proton field because it has a much smaller density. It adds little to the proton-electron repulsion, since, due only to surface area, it diminishes so quickly with distance from the electron. But it does act to repel other electrons. Electrons repel not because they have the same charge, but because they have the same size, or scaling. The electron emission field is not powerful enough to affect protons, but it is powerful enough to affect other electrons. This is the main cause of exclusion. An electron in an orbit actually excludes all other electrons from that orbit, but only electrons with the same four numbers try to inhabit the same states, so the first electron will only have to exclude electrons just like it. Imagine you are a rabbit in a hole. You may have the ability to bite any intruder, but you will only bite intruders that come into the hole. The hole is just the right size for a rabbit, so you only have to bite other rabbits. You could bite badgers and bears and elephants, but they see how small the hole is and do not try to climb into it. Now, any blind person monitoring your hole would hear only the squeals of the rabbits you were biting, and he might come to the conclusion that you only exclude other rabbits. But the truth is, you only have to exclude other rabbits.
The Planck Relation and the Mass of the Photon
The Planck relation is just an equation relating the energy of a moving particle to its frequency, via the de Broglie wave. The particle does not have to be a photon; it can be any quantum, like an electron.
E=hf
Where h is Planck's constant. However, since MM has shown that Planck's constant is hiding the mass of the photon, we may now unwind this equation, finding much more information buried beneath it. Using simple mechanical postulates, MM has calculated that the mass of the infrared photon is h/2,400. To find this, MM simply used G to scale down from the proton mass. You can also use the Dalton, 1821, to find this same mass. Simply cube the Dalton and invert it. The Dalton is an outcome of spin mechanics, and the photon is three levels below the proton and two levels below the electron. Using the Dalton, you will get 2,400, but using G will require you multiply by an additional 2.5. This is because G is a scale for size, not mass, and the density of the photon is not equal to the density of the proton.
If we apply these new findings to the Planck relation, we see that the relation is between mass and energy, just like Einstein's equation E=mc2. And this means that the dimensions of h have been hiding something. Planck's constant is given complex dimensions to account for the transform to f, but if h contains a photon mass, then we are really transforming E into a mass, a frequency, and x:
E = xmc f
Let us apply the equation to the photon itself, to begin with. In that case
x = cλ
E = mc cλf
cλ = 2,400
λ = 8 x 10-6m
Which is the infrared photon MM chose to begin with.
E = mc cλf = mc2
Yes, Planck's relation is just a restatement of Einstein's equation, but the two together are used to hide the mass of the photon. The standard model forbids you from applying Einstein's equation to the photon, or from seeking this photon mass in the Planck relation. Why? Because that would mess up their gauge math.
We can do the same thing for the electron:
E = ½ me vλf = ½ mev2
h = ½ me vλ
The mass of the electron is 3.3 x 106 times greater than the mass of the infrared photon, so vλ must be much less than cλ.
vλ = 2h/m = .00146
In the famous Davisson-Germer experiment of 1927, electrons were fired at a crystalline nickel target. We are told they were slow-moving, but are not given a velocity. We may now calculate it directly. The wavelength was measured from the experiment to be .165nm, which makes the velocity of the electrons 8.8 x 106m/s or .03c. Not so slow.
One really have to ask why the standard model refuses to write the equations this way. Why do they refuse to show the simple mechanics and math as shown above? The answer, again, is to save their gauge math, a math that already contains its own fields and symmetries. They have tried to match nature to the symmetries, but that has never worked for them. Math needs to match to nature, rather than nature to math. They have already had to break their gauge symmetries to match experiments. If the gauge symmetries require breaking, then the matrices must have been wrong to start with. And if that is so, then the gauge math should be ditched as a whole.
Physicists are so in love with tools that do not work. It is as if they have a pathological obsession for the patches themselves. The modern physicist is like a carpenter in love with a golden hammer whose handle is cracked. The gold is too soft to work, and the head flies of with every swing; but the carpenter must use it and nothing else, since he has convinced himself that the shine of it is what generates his business.
Addendum [February 2010]: we can use the above math to discover what quantum Planck's constant is really hiding. MM has said that Planck's constant is hiding the mass of the photon, but since photons have different energies, we may ask which photon it is hiding. Well, we can see from above that h = mcλ. So we just make cλ = 1, and we will have h = m, you see. The photon that has a wavelength of 1/c is a photon with a wavelength of 3.3 x 10-9m, which is an X-ray. Since current physics is using h as the quantum of action, they must be using the X-ray as a quantum. This is not logical. It is much more logical to use the charge photon as a quantum. We should be using the infrared photon as the field quantum, not the X-ray.
The Fine Structure Constant
In his book QED, Richard Feynman has a final chapter called “Loose Ends” where he tells his audience some of the remaining unknowns of the theory of quantum electrodynamics. Chief among these is the number 1/137.03597, which is the fine structure constant. Feynman calls it the observed coupling constant or “the amplitude for a real electron to emit a real photon.”1 But at a place like Wikipedia, you will find it listed under “fine structure constant.” Feynman says that “all good theoretical physicists put this number up on their wall and worry about it.”
This is just more misdirection. Feynman says that “a good theory would say that e is the square root of 3 over 2 pi squared, or something.” Yet MM has an even better theory: The constant is a fake number: an outcome of math specifically designed to keep you from looking in the right place.
The standard model defines the fine structure constant like this:
α = e2/2hcε0 = e2cμ0/2h = 2πke2/hc
Modern physics loves to bury mechanics under constants. As you can see, the fine structure constant, which is already a constant, is defined in terms of other constants, like the permittivity and permeability constants. Charge is also now buried under many other constants, including the Rydberg constant, the Josephson constant, Faraday's constant, Avogadro's constant, and more. Now, we do not want to have to fool with the permittivity constant or the vacuum permeability, which are misdirections (See . So we will look at the third equation.
α = 2πke2/hc
At first it is difficult to see what Feynman is asking. He asks why the number is 137, but in the first instance, it is 137 because of the way the equation is built. So why is the equation built this way? You can see that we have Coulomb's constant, but since we are dealing with quanta, we do not need it. In Coulomb's equation is a Unified Field equation in disguise MM has shown that Coulomb's constant is a scaling constant, taking us from the quantum level to our level, but this equation isn't scaling anything to our level. Although light is going c relative to us, it is also going c relative to the quantum level. Both the electron and photon are already at the quantum level, so to me the presence of k is a sure sign that these physicists do not have any idea what they are doing. This is why it is obvious that this fine structure constant is a ghost.
The only physically assignable variables or constants we have here are e and c, so Feynman must be asking why the relationship of c to the squared charge of the electron is what it is. Notice that the “coupling” is between a squared charge and a velocity. That's rather odd, wouldn't you say? For the coupling constant to be meaningful as a number, it should couple a mass and a mass, or an energy and an energy, or something like that. As it is, this number is just an outcome of a juggled equation, juggled purposely to hide the real interactions.
This fine structure equation, with h and k, is already too complex. But it was not complex enough for modern physicists, who were afraid some graduate student might unwind it. So in the decades since they have created even more complex equations, like this one:

Where R is Rydberg's constant
Every decade, basic physics and mechanics is plowed under by more and more needless math.
Feynman's question should have been, what is the relationship of the electron's mass to its charge, or what is the relationship of the electron's energy to the photon's energy. He and his colleagues could not answer these questions because they had already buried them under so much math, but MM can answer them quite easily. To do that, we first have to dig Planck's constant out of the rubble and show what it really is.
If we go to the Wikipedia page on Planck's constant and scroll down to the section called “origin of Planck's constant,” we find that Planck himself had no idea of the value of the constant. He was working, like Newton before him, with proportions. In looking at Wien's displacement law, Planck proposed that the energy of the light was proportional to its frequency, and then simply made up the equality with his constant. In other words, he had no idea where the constant was coming from. Planck did not develop the equation from mechanics, he developed it from experiment: specifically, the experiments at the turn of the century on black body radiation.
That Planck had no idea where his constant was coming from is understandable, but that later physicists could not figure it out is beyond belief, especially after Einstein gave them the equation E=mc2. Planck's constant is now taught as a conversion factor between phase (in cycles) and action. But action is an old feint: a longstanding blanket over mechanics. So we can ignore that. The constant is expressed in eV seconds, erg seconds, or Joule seconds, all of which are unhelpful mechanically, so we can ignore them as well.
Here is the derivation of Planck's constant to show how easy it is to derive mechanically and what makes it astonishing is that the derivation is not on the Wiki page or in any textbooks. Once you see how easy it is, you will agree that this information must be hidden on purpose. There is no way that a century of particle physicists could have been ignorant of this proof, so we must assume they were hiding it with full intent to deceive.
We take Einstein's famous equation and apply it straight to the photon. We do not need the transform gamma: gamma applies to everything except light. Light is a special case, remember? Einstein's postulate 2? So we can apply the equation as is, with no transform.
E = mc2
c = λν
E = m( λν)2
h = m λ2ν
Now, take a common photon like the infrared photon, with a wavelength of about 8 x 10-6 m. In that case λ2ν = 2,400. So,
h = m(2,400)
Planck's constant is about 2,400 times the mass of the photon.
As to why, contrary to the mainstream, that photons have mass, see Unifying the Photon with other Quanta, How they Travel and why they go c. There MM developes a mass for the photon without using Einstein's equation. It will be done here again. We start with the difference between the mass of the electron and the mass of the nucleon, which is called a Dalton, and which is about 1821. MM has already shown that this number comes from stacked spins on the electron. (See The Unification of the Proton and Electron & Finding the Electron Radius & The Fallacy of the Electron Orbit.) There MM developed an equation that yields not only the Dalton but all the meson levels as well. Thus the mechanical explanation of the number 1821 is presented with simple math and simple motions. In fact this same quantum equation will give us the photon mass as well, by assuming the photon inhabits a fundamental level of the equation, just like the electron, nucleon, and all the mesons. This fundamental level is 18213 beneath the proton level, or 18212 beneath the electron level. All we have to do is multiply the proton mass by 1/18213, which gives us:
1.67 x 10-27(1/1821)3 = 2.77 x 10-37 kg
That is the mass of the photon, derived without Einstein's equation. So my math is not circular.
But is it the correct math? Let's see. If we multiply that mass by 2,400 we get 6.63 x 10-34 kg, which is, sure enough, the number value of Planck's constant.
I have proved my point. Planck's constant is hiding the mass of the photon.
Now to answer Feynman's question, we have to go back to the fine structure constant and remove all the fudge.
α = 2πke2/hc
In Gravity at the Quantum Level MM showed that k is a ghost and in π (pi) is 4 not 3.14 that π is also a ghost, and since it was shown h and α are ghosts, we can dump them. We will use their numerical value to absorb them into the equation.
e2 = hcα/2πk = 2400mc(.0073)/5.65 x 1010 = .091m
e = .3√m
e = 1.602 x 10-19 C
1C = 2 x 10-7 kg/s (see definition of Ampere to find this number in the mainstream)
e = 3.204 x 10-26 kg/s
e = 6.08 x 10-8[√kg)/s](√m)
So, Feynman's question becomes “How do we explain this numerical relationship of m to e?” Well, we can't do it from these equations, as you now see, since these equations are not giving us a number relation between m and e. They are giving us a number relation between m and e2. To get the right dimensions for e, the dimensions for that last constant must be √kg)/s. Since there is not a 1-to-1 relationship between s and √kg, even that last number is not telling us what we want to know.
We have more work to do. Let's look first at that number for e in the next to the last equation, which is the current one is expressed it in kg/s, and this brings a lot of things to light. Remember that the electron has a mass of 9.11 x 10-31 kg. According to this equation the electron is emitting a charge every second that outweighs it by 35,000 times. The electron is emitting the mass equivalent of 35,000 electrons every second, or 1.16 x 1011 photons per second. So it is not just my charge field that has mass. The standard model charge field has a huge mass, it is just hidden by these dimensions like the Coulomb. Ask yourself why the standard model and textbooks never write the fundamental charge as kg/s. Textbooks tell you that charge is mediated by virtual photons, but they do not tell you that the electron emits 35,000 times its own mass of these virtual photons every second, just to create charge. You see, if they told you this, they would have to field your next question, which is, “How can the electron emit so much mass and not dissolve? How does this conserve energy?”
In MM's theory, he puts that question out in the open and tries to answer it, but the standard model prefers to dodge it with all their sloppy math and undefined constants and complex dimensions like the Coulomb and Ampere and Volt. [See MM's papers The Galactic Rotation Problem & How Dark Matter Fudged and the Bullet Cluster on his site to see how MM uses this math to solve longstanding problems in astronomy.]
What allows us to solve this easily is the loss of the constant k. Remember that k is a scaling constant, and we do not need it here. The reason is because in these equations we are comparing quanta to each other so that no scaling is involved. For the same reason, we can import a trick that was used in Gravity at a Quantum Level, where MM showed that as long as we are staying at the quantum level, and not scaling, we can use a very familiar number for gravity at the quantum level. If we are measuring gravity at the quantum level from our level, then we have to scale down using the radius as the scaling transform. But if we are not scaling, we can use 9.8 m/s2 as the number for gravity. MM showed that if the quanta measure their own gravity, this is the number they would get. It sounds crazy, but MM will show how it works again here. We just find a unified field force for the proton, using its mass and its acceleration.
F = ma = (1.673 x 10-27 kg)9.8 m/s2 = 1.639 x 10-26 N
Multiplying by two to represent the vector meeting of the fields of both electron and proton gives us 3.279 x 10-26 N. Amazingly close to our bolded number above for e, isn't it?
You will say “Yes, but you have a pretty significant difference, 7.5 x 10-28 N. You also have the wrong dimensions. The elementary charge is in kg/s, and your number is in N.”
Let's look at my margin of error, first. If we divide, we find MM's error is about 2.3%. But MM has already shown in Bohr's Three Mistakes and Millikan's oil drop experiment on his site that the Earth's charge field is skewing all experiments done on the Earth.
It is responsible for the .1% difference between the Bohr magneton and the magnetic moment of the electron. It was responsible for Millikan's error. And so it must also be responsible for a .1% error in computing quantum masses. The proton's mass is determined in experiments done here on the Earth, and physicists have never included the effect of the Earth's charge field, since they do not know it exists.
You will say, “Your error is 2%, not .1%”. First of all, it is not my error: it is the standard model's error. And the error enters this problem in multiple places. Just as in Millikan's oil drop experiment, we have a confluence of errors. Let's look at the mass spectrometer, used to “weigh” the proton:
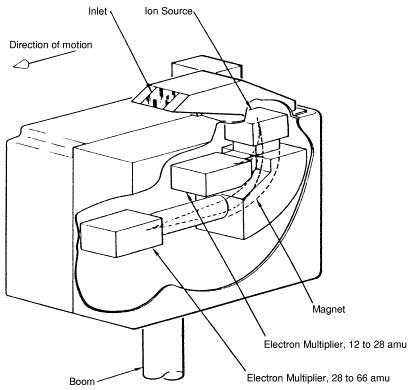
As you can see, the spectrometer must suffer the same problems as the oil drop experiment, since the magnet is in the plane of the Earth's charge field. The ions are moving straight down to start with and have a downward vector throughout the experiment. This can't work. The magnetic field is also rather weak, so it has no chance of burying the error simply by field strength
But even if the machine is turned 90o, so that all motion is horizontal instead of vertical, the problem will remain. As shown in The E/M Fields of Solar System Bodies on his site, unlike Venus, the Earth is both electrical and magnetic. If the experiment is done vertically, the electrical field of the Earth interacts. If the experiment is done horizontally, the magnetic field interacts. Both fields have the same strength, as produced by the charge field, so you are damned either way.
Although the mass spectrometer, either horizontal or vertical, must encounter the Earth's charge field, it does not encounter it precisely like the oil drop experiment did. Millikan set up the his electrical field in vector opposition to the gravity field, and included gravity in his calculations. But the math of the mass spectrometer attempts to ignore gravity, as an experimental constant. Masses in mass spectrometers are not calculated from gravity (in the experiment), they are calculated relative to each other. Wikipedia admits that “there is no direct method for measuring the mass of the electron at rest,”2 and this is also true of the proton. You can see that the proton must be moving in the spectrometer, and its path must be bent by a field. The relative bend then tells us the mass.
At any rate, gravity is present throughout the experiment, and though it can be ignored as a matter of relative mass, it cannot be ignored mechanically. Because it is present, it must be included in any correction. Both it and the induced magnetic field are affected, but because they are not in vector opposition we do not treat them the same as we did with Millikan. With Millikan, we applied the charge field correction directly to his electrical field, since he aligned them. Here we halve the correction and then take the square root to square the effect. We halve the correction because the motion of the particle in the curve goes from (nearly) all gravity to (nearly) all induced magnetic field.
Look at the curve in the diagram. At the end of the path, the particle is not moving down at all. So we go from “gravity is the entire cause of motion” to “gravity is almost no cause of the motion.” If we sum that path, from all to none, all being 1 and none being 0, then the average will be about ½, given a smooth curve. So we only get half our error during the experiment. We only get half of it, but we still have to take the square root, since the error affects both the gravitational field and the induced magnetic field. Two effects will give us an increased total effect.
The charge field of the Earth is .009545 m/s2, which is .0974% of gravity. Half that is .000487, and the square root is .0221 or 2.21%. Above, my error was 2.3%, so MM is now within .0009. The rest of that error is probably due to MM's math alone, since, as a theoretician, he almost never carries his calculations past the thousandths place. Those who love precision can fine tune the math.
Now let's look at the dimensions. There is a force; the standard model Coulomb reduces to kg/s or Ns/m. But remember that the standard model is not too picky about its dimensions. The cgs system is still used, and in that system charge was kg or Ns2/m. Yes, before SI, charge used to reduce to mass, although they never promoted that fact. So the dimension changes with the system. It changes again with MM's system, so that charge is a force, not a mass. The dimensions can be changed without changing the number, because s/m reduces to one in MM's mechanics.
Charge is the mass of the photon field, but a mass cannot give us a strength of interaction or a force by itself. You need a mass and a velocity, This will give you a field strength, which will give you a force. Velocity is m/s. If you multiply s/m by m/s, you get one, and the field dimension reduces to N.
But what does all this mean for the fine structure constant? It means that the number for the fine structure constant comes from misusing Coulomb's constant in quantum equations. In the equations we looked at above, k should never be used, so the defining equations for the fine structure constant are just garbage. The only way to understand what the fine structure constant is, is to look at the impact parameter equation of the Rutherford formula. (See The Atomic World is 100 Times Larger Than We Thought.) If you take that link you will see that the fine structure constant is just a transform or scaling constant between mass and charge.
Mass and charge have been defined in two different ways, by two different sets of field equations, but they are actually equivalent. The fine structure constant just takes us from one to the other. But again, if we didn't have the constant k fouling up field equations at the quantum level, we wouldn't need the fine structure constant at all. My own unified field equations rewrite all charge as mass, jettisoning the redundant field equations of charge. Of course this allows one to jettison k and the fine structure constant as well. That is what was shown above, by finding the correct numbers using Newton's equations like F=ma instead of electrostatic or quantum field equations. To make the unified field equations completely mechanical and transparent, we have to jettison all mention of the old charge equations, since they weren't mechanical. All classical and quantum E/M equations quickly devolve or dissolve into virtual fudges and finesses, swept out the door forever. All E/M field theory, quantum and macro, has to be rewritten in terms of volume, density, and real particles with real size, as was done here.
Conclusion
The elementary charge is not a charge, it is a unified field force as in Newton's law is a Unified Field of Gravity and E/M. The standard model believes that forces at the planetary or astral level are all gravitational and at the quantum level are all E/M, but this is false. The forces at all levels are unified field forces. The elementary charge includes gravity. For this reason we can use Newton's equations at the quantum level. Newton's equation is a unified field equation, and if we use it correctly, we can use it at any level. The measured masses of quanta are unified field numbers. All masses are unified field numbers, since they represent compound motions and forces. Quantum masses are hiding both fields, and this allows us to calculate “charges” straight from masses, without Coulomb's equation and without Planck's constant.
The elementary charge is not only a unified field force, it is a compound of emission by both the electron and the proton. Even when we are measuring the charge of the electron alone, the field will be composed of proton and electron emission. You cannot study electron charge alone, or proton charge alone, since you cannot go anywhere in the universe where the charge field is unipolar. Even on the surface of the proton or electron, you will find a bi-polar field. The charge field is everywhere, and it its strength is everywhere determined by compound emissions.
For the record, this is also why you can't have a magnetic monopole in the real world. There are no walls: the charge field is everywhere, and it is everywhere created by both protons and electrons (and anti-protons and positrons).
For a different and slightly simpler explanation of where the fine structure constant comes from, you may also consult my paper on Rutherford's scattering equations, where MM showed that the atomic world is about 137 times larger than we think.
1QED, p. 129.
2http://en.wikipedia.org/wiki/Planck%27s_constant
The Fine Structure Constant is a Mass to Charge Transform
,Here it will be shown that the fine structure constant is a mass to charge transform, and tie it to other important charge numbers.
The fine structure constant is currently defined as the amplitude (or probability) that an electron will emit a photon.
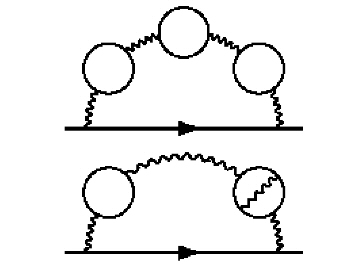
Underneath the Feynman diagram above, Wikipedia says this:
Two example eighth-order Feynman diagrams that contribute to the electron self-interaction. The horizontal line with an arrow represents the electron while the wavy-lines are virtual photons, and the circles represent virtual electron-positron pairs.
"Virtual photons" are the sign of a fudge. Virtual particles are not physical, so they are infinitely pushable. This despite the fact that Feynman himself defined the fine structure constant as “the amplitude (or probability) that a real electron will emit a real photon.” Apparently they could not make that work in the gauge math, so they have fallen back onto the virtual photon, which is a ghost. But we do not need any eighth-order Feynman fudges, since the fine structure constant isn't an amplitude or a probability to start with. It will be shown to be a simple mass to charge transform.
Even Feynman understood that his pushes were pushes. In one of his last books, QED , Feynman told us he put the fine structure constant on his blackboard every morning and stared at it, hoping to crack it like one of his safes. He admits he never did. He never figured out why it was the number it was, or the mechanics underneath it. That is why the mainstream is still diddling with the Feynman diagrams, which are just heuristic devices. No one after Feynman had cracked that safe either, until MM came along with the actual combination.
In current math, the fine structure constant is mainly another fudge since it can be derived by simplifying and correcting basic quantum equations. In the first paper The Atomic World is 100 Times Larger Than We Thought MM derived it by correcting Rutherford's impact parameter equation. in the previous section on the fine structure the fine structure constant defining equations were torn apart, showing how they were overwritten and redundant.
Here, MM extends his analysis into new territory, refining even further the significance of the number 1/137 by tying it to new numbers MM has derived in the charge field.
First, let us review the major findings so far. It was shown that the mass of the alpha particle in the Rutherford experiments was inhabiting the equations in a strange way. Rutherford wrote the impact parameter equation as a charge equation, but then inserted the mass of the alpha particle without transforming it into a charge entity.
b = √ [1 + cosθ /1 - cosθ ] kQq/mv2
Where b is the impact parameter. If we study the form of that equation closely, we find that the field in the numerator of Rutherford's equation doesn't match the field of his denominator. The numerator is written in terms of charge (as we see from q and the constant k), while the denominator is written as mass. The kinetic energy mv2 is not a charge entity and can't be included in a charge equation without transforming it into a charge entity. What we need is a transform from mass to charge, to correct the equation and make the numerator match the denominator. MM found that this transform just happened to be the fine structure constant.
That's right: what Rutherford needed was a way to write the alpha mass as charge. In Coulomb's equation is a Unified Field equation in disguise MM showed that charge and mass were actually equivalent, this was not hard for me to do for him. To transform the alpha mass into charge, we simply create a photon with the same energy as the alpha, and then calculate its mass equivalence from the equation E=mc2 . We can use that equation without gamma because we are applying the equation to a photon. Relativity doesn't apply to photons, according to Einstein's Principle 2. Relativity transforms everything except light. Light is the cause of Relativity, so you cannot transform light itself.
The mass of that created photon with the same energy as the alpha is the charge equivalence we need to correct the Rutherford equation. The alpha mass is not a charge entity and so it cannot inhabit a charge equation. But the mass of the equivalent photon is a charge entity, and can.
And the ratio of the mass of that created photon to the mass of the alpha is the fine structure constant:
mγ/mα = .0073
In other words, we multiply the mass of a particle by .0073 to find its charge equivalent. The fine structure constant is a mass to charge transform. It is also a transform between normal matter and light. It tells us that at equal energies, light is that much less massive than normal matter. The greater velocity of light makes up the energy difference.
This must imply that the fine structure constant is not a relativistic number, meaning it wouldn't apply to normal matter at extremely high speeds. The fine structure constant only applies to normal matter that is at zero or non-relativistic speeds. This is a complication that the mainstream has so far missed, and is another cause of current equations misfiring and requiring renormalization and other pushing.
If we compare what we found by correcting the Rutherford equation to the current definition of the fine structure constant, we find that the constant cannot be what we are told it is. There is no electron in the Rutherford equation. Rutherford is using the mass of the alpha, which is a Helium nucleus, not an electron. An electron is a beta particle, not an alpha particle. The fine structure constant is not a probability of any sort, it is a mass to charge transform, or a matter to photon transform.
Now, in The Galactic Rotation Problem & How Dark Matter Fudged MM has shown that photonic matter outweighs normal matter by 19 to 1, in most charge situations and as a universal average. This is where the dark matter ratio of 19 to 1 or 95% is coming from. If we divide 137 by 19, we get 7.21. Here's a question for my regular readers: where does that number come from? Where have we seen that number in my other new equations? I'll give you a hint: it was in my first book. It is the difference between level 1 and level 2 in my quantum spin equations.
In The Unification of the Proton and Electron & Finding the Electron Radius & The Fallacy of the Electron Orbit MM found that the electron with x-spin will have an energy 7.22 times the energy of the electron at rest. If the electron at rest is given a baseline energy of 1, the energy level of the x-spin will be 7.22. MM has called that the first mesonic level, and it is the level between electron and muon.
What is the connection? The connection is that charge is giving the electron its x-spin. A free electron in a charge field will be given an x-spin by the field, and will gain 7.22 times its original energy. Why? Because the charge field is bringing the electron up to its own energy level. The charge field has 19 times the mass equivalence of the electron at rest; but—at equal energies—charge has 137 times less mass. So to bring the electron up to the energy of the charge field being recycled though it, we have to increase its energy by 137/19 = 7.2. Once the electron has been given an x-spin by the charge field, it is in equilibrium with that field.
This now provides us with a third derivation of the fine structure constant, and this last one is the shortest and most transparent. Since MM has shown short mechanical derivations of both 19 and 7.2, we see precisely where the number 137 comes from. It is just 19 x 7.2.
You will say, “If 137 and 19 are mass differentials, shouldn't 7.2 also be a mass differential? But in your unification paper, you say 7.2 is an energy differential.” Good point, but easily answerable. Since 137/19 is a ratio, it doesn't matter if the numbers stand for mass or energy. Since mass and energy are proportional, the ratio will be the same either way. In other words, we could change both 137 and 19 into energies, then find the ratio, but since we would be multiplying both 137 and 19 by the same number, the ratio would not change. Therefore my equation is correct.
More on the FINE STRUCTURE CONSTANT
First published January 23, 2016
MM has already published several papers above this topic , suggesting the fine structure constant is a proportionality constant between the electron and the photon; or, to say the same thing in a different way, it is a charge to mass transform. Or, to say it in a third way, it is a light to matter transform. We will find the same thing here, but come at it from a completely different angle.
The number in question is 137, so whenever I see the number 137 come up in quantum calculations, my first suspicion is that it must be related to the fine structure constant somehow. Yes, numbers are sometimes just coincidences, but many important connections have been written off as coincidences, both in physics and out of it. So my first assumption is that number relations are NOT coincidences. If they are, fine. If they aren't, then I will have discovered something important, you see.
MM has weighed the charge field in various ways over the years, including most importantly in my papers connecting the charge field to so-called dark matter The Galactic Rotation Problem & How Dark Matter Fudged. MM has shown that the mainstream dark matter numbers are telling us the charge field outweighs the matter field universally or generally by 19 to 1. They are also telling us the proton is recycling 19 times its own mass in photons every second. But MM was looking for another way to weigh the charge field, and MM recently saw another way to do that. That is what this paper is about.
In both mainstream theory and my theory, there is a discrepancy between the atomic mass unit and the mass of the proton. The atomic mass unit is about 1823 electron masses, while the proton is about 1836 electron masses. In MM's preious papers, he has called the AMU the Dalton, and that is fairly standard since the mainstream does that, too. The problem is, the Dalton is supposed to be the mass of a nucleon; but, again, that doesn't work out because the neutron is actually heavier than the proton. As you see, that just makes the problem worse. Mainstream theory usually buries this problem, but when it does address it, it just uses it to blow more esoteric smoke. As usual, there is no straightforward mechanical explanation for it.
MM's assumption has always been that the difference is actually the mass of the charge being recycled. Since the mainstream doesn't know about charge recycling, of course it can't support this line of reasoning. In mainstream theory, charge, like photons, has no mass. However, even in mainstream theory this charge should at least have mass equivalence . If charge is real, it must have energy, and all energy has mass equivalence. But in my theory, it is even more transparent than that. My photons and charge do have real mass. MM has calculated this mass, and it falls just below the mainstream lower limit for mass on the photon. In other words, they have run experiments and long equations, coming to the conclusion that the mass of the photon must be below 10-36 kg. Using the same experiments but extrapolating from different (and older) mainstream equations [including Newton's gravity equations and the constant G], MM has calculated the mass of the photon at around 10-37 kg. At any rate, since charge must have mass or mass equivalence, and since photons travel at a finite velocity of c, during any real time the proton must be recycling a given number of them. At any given dt, there will be some amount of photons passing through the proton. It is these photons that have failed to have been weighed so far in the equations. And it is these photons that are causing the differential between 1823 and 1836.
To show this, let us work the equations backwards, as is so often useful in my analyses. However, rather than use the mainstream's number for the Dalton, MM is going to use his own, taken from my paper showing how to build quanta with stacked spins. In it, MM provides the quantum spin equation that shows how to add spins to an electron to create a proton. In it, MM finds a value for the Dalton of about 1821. There is a miss of about .001 between my value and the mainstream value, and that is because the mainstream is including the neutron in its calculations and I am not. MM's Dalton is not exactly what theirs is. Their Dalton is an average while mine is a direct spin-up of the electron. In my equations, I am finding the volume of the stacked spins through which the photons must travel as they recycle through the baryon. But MM is not including the actual charge passing through that volume.
Now, if we subtract 1821 from 1836, we get 15. That tells us that when we “weigh” a proton by conventional methods, its weight includes the charge passing through it. And that charge weighs the equivalent of 15 electrons. Now, the number 15 doesn't look so interesting, but if we multiply it by the mass of the electron in kilograms, what do we get?
{eq. 1} 9.11 x 10-31 kg x 15 = 137 x 10-31 kg
Curious, no? MM will be told that is a number coincidence. But notice that we have just found that the mass of the charge moving through the proton is 137 x 10-31 kg. Again, the mass of the charge . So we have just done another charge to mass transform, as we did in other papers studying the fine structure constant. So it is very unlikely the number 137 is a coincidence here. In fact, I can show it isn't.
In that MM's previous paper above, MM showed the fine structure constant was a charge to mass
transform, and its value could be expressed as the mass of a particle relative to an photon with an
equivalent energy. In the Rutherford experiment, that particle was an alpha.
mγ/mα = .0073 = 1/137
MM predicts he can manipulate that equation, easily achieving the eq. 1 above with the 137 in it. Here goes:
E/c2//mα = .0073
mα c2/E = 137
(6.64 x 10-27kg)c2/E = 137
multiply both sides by 10-31
(6.64 x 10-27kg)(9 x 10-15m2/s2)/E = 137 x 10-31
(6 x 10-41kgm2/s2)/E = 137 x 10-31
E = 4.38 x 10-12 J
Was that the energy of the alpha particle in Rutherford's experiment?
It wasn't known then, but it has since been measured using the so-called Coulomb barrier. Rutherford was using gold, atomic number 79.
Yes, because that is about
27MeV, which is the known energy of the experiment.
Which means, we can reverse the equation a couple of lines back to this:
(6.64 x 10-27 kg)(9 x 10-15m2/s2)/E = 137 x 10-31
Multiply both sides by 1 kg
(6.64 x 10-27kg)(9 x 10-15m2/s2)kg/E = 137 x 10-31kg
Now write the alpha mass as a function of the electron mass
(4)(1822)(9.11 x 10-31kg)(9 x 10-15m2/s2)kg/E = 137 x 10-31kg
That is just an expansion of eq. 1, as you see. And that tells us
(4)(1822)(9 x 10-15m2/s2)kg/E = 15
(4)(1822)(1 x 10-31)kg c2/E = 15
(4)(1822)(1 x 10-31)kg c2/4.38 x 10-12 J = 15
(4)(1822)/(487) = 15
So you can begin to see how the numbers fit together. This proves that the number 137 coming up in both places was no accident. I have connected the two derivations, showing exactly how the number 137 coming out of Rutherford's experiment causes the number 137 in my calculation. This is yet more confirmation that my analysis is correct, and that the gap between the numbers 1821 and 1836 is caused by the weight of the charge recycling through the proton. The proton is recycling the equivalent of 15 electrons during every spin cycle.
So you can begin to see how the numbers fit together. This proves that the number 137 coming up in both places was no accident. I have connected the two derivations, showing exactly how the number 137 coming out of Rutherford's experiment causes the number 137 in my calculation. This is yet more confirmation that my analysis is correct, and that the gap between the numbers 1821 and 1836 is caused by the weight of the charge recycling through the proton. The proton is recycling the equivalent of 15 electrons during every spin cycle.
You will say, “I thought you said the proton was recycling 19 times its own mass every second. Now you say it is recycling .008 of its mass. Which is it?” Both. MM didn't say a spin cycle takes exactly one second. No, we can calculate the time of one spin cycle from the numbers above. Obviously, from those numbers, one spin cycle only takes about . 00043 seconds.
In closing, MM will answer one last question. A reader might ask, “If photons are recycling through the proton, they must be deflected somehow. But what is the proton wall made of?” I know this is going to sound esoteric and spin your head, but it isn't esoteric. The wall is made of nothing. It isn't a wall, it is a boundary. It simply the boundary with the ambient or external charge field. The internal photons are being deflected by. . . external photons at the boundary. Remember, we have discovered the charge field outweighs the matter field by 19 to 1, so the ambient field is quite rich. It may seem empty at our size, but at the size of the proton, it is quite full. The protons are 1014 times closer to the photon size than we are, so photons seem that much larger and denser. Charge is incredibly powerful at the quantum level, and the mainstream knows that. It is perfectly capable of acting as a wall here, although it will come as a surprise to most.
My reader might respond, “I still don't understand why the internal photons can't just go back into the ambient field anytime they like. What is stopping them? Haven't you said photon fields are mostly interpenetrable?” Yes, in space , they are mostly interpenetrable. But MM never said they were interpenetrable at the proton boundary, or even the nuclear boundary. When we get down to the quantum level, we have dense vortices of photons, and they are perfectly able to exclude one another at those densities. At that level, we get a high number of photon collisions, and those collisions are perfectly capable of creating strong boundaries. Specifically, at the border of the proton, the boundary is caused by spins that cannot add or subtract. For photons to spin interact, the spins have to be very close to matching or opposing. If the spins are “sideways” to one another, the only thing the photons can do is deflect. When a particle like the proton is in a tight spin relative to the ambient field, photons coming in from that field cannot spin interact with photons already trapped inside the particle. The spins are almost always orthogonal, and the only interaction is a deflection at a small angle. This keeps the photons inside the particle from escaping into the ambient field through the boundary.
The Fine Structure Constant Again
by Miles Mathis
First published November 14, 2018
In the Bohr Magneton paper of many years ago, MM made many corrections to Bohr's old equations,
k
including correcting the angular momentum equation L and dumping improper use of at the quantum
level. In so doing, I showed the Bohr radius could be found by the simplified equation
r = √(e2/mc) = 9.69 x 10-9m
That is about 177 times larger than the current radius. Because that is such a huge correction, one that seems to conflict with some known data, my correction was ignored. This despite the fact that I was able to later use the correction to solve the vacuum catastrophe and other big problems. These big problems require big corrections, obviously, but the mainstream is still not ready to admit that. Well, my Bohr radius is so much larger than the mainstream's because it isn't really assigned to the same thing. Not only does the mainstream have the wrong number, they have the wrong assignment. They assign the Bohr radius to the orbital, but I have shown there are no orbitals of that sort at all . Yes, electrons do link up to the nucleus, but they pair up with individual protons in the nucleus. They do not orbit the nucleus as a whole. And I have shown their actual positions are very much closer than the Bohr radius, being right on the nuclear boundary. What the Bohr radius always signified was the radius of electron capture, and that is what it stands for in my theory. This is the effective limit of the charge field of the nucleus, and the Bohr radius should signify the boundary of the nucleus' normal charge effect on passing electrons. This explains why the radius is larger than the current radius, and why it does not conflict with data showing “bound” electrons much nearer the nucleus.
Anyway, at the time MM tried to link that directly to the fine structure constant 137, but as it turned out the problem is a bit more complex than that. To get 137 from 177 requires a bit more unwinding. I had both the math and the field theory to get it done then, but for whatever reason it didn't happen. In other early papers , I showed that Newton's gravity equation and Coulomb's electrostatic equation were roughly the inverse of one another, with the constants working in much the same way. However, in the first equation G was acting as a scaler, scaling the atomic field down to the charge field. In the second, k was scaling the charge field up to the atomic field. But since the numbers were not the exact inverse of one another, no one saw that before me. There is a difference of about 1.67 between G and 1/k .
However, in the Bohr paper MM also solved that mystery, showing that to match the method of G, Coulomb should have scaled the quantum field up to 1 meter. Instead, he scaled it directly to his data in that specific experiment, where his pith balls were only around 6mm. That created an error in k of. . . 177.
In a later paper above on the fine structure constant , MM did the math, showing where the difference between 137 and 177 comes from. The difference between 137 and 177 is simply √(Gk ). In other words, if we assign the number 177 a letter, say β , then α, β , and G, are not constants, they are transforms, scalers, or corrections. We have seen that they are size specific as well as experiment specific. This allows us to see that 137 and 177 don't match for the same reason G and aren't simply the inverse of one another. G is not 1/k . We have a difference of 1.67. So, mathematically, the fine structure constant is a simple result of G, k, and β. You know what G and k are, and I have shown you above and in previous papers that β is both the error in the Bohr radius and the error in the charge density. So,
√(Gk) = 137/177
or
137 = 177√(Gk)
This answers Feynman's biggest question in the simplest manner possible.